DAC - Parámetros Estáticos
El Convertidor Digital-Analógico (DAC) es un dispositivo que convierte una secuencia de datos de entrada digital en señales analógicas.
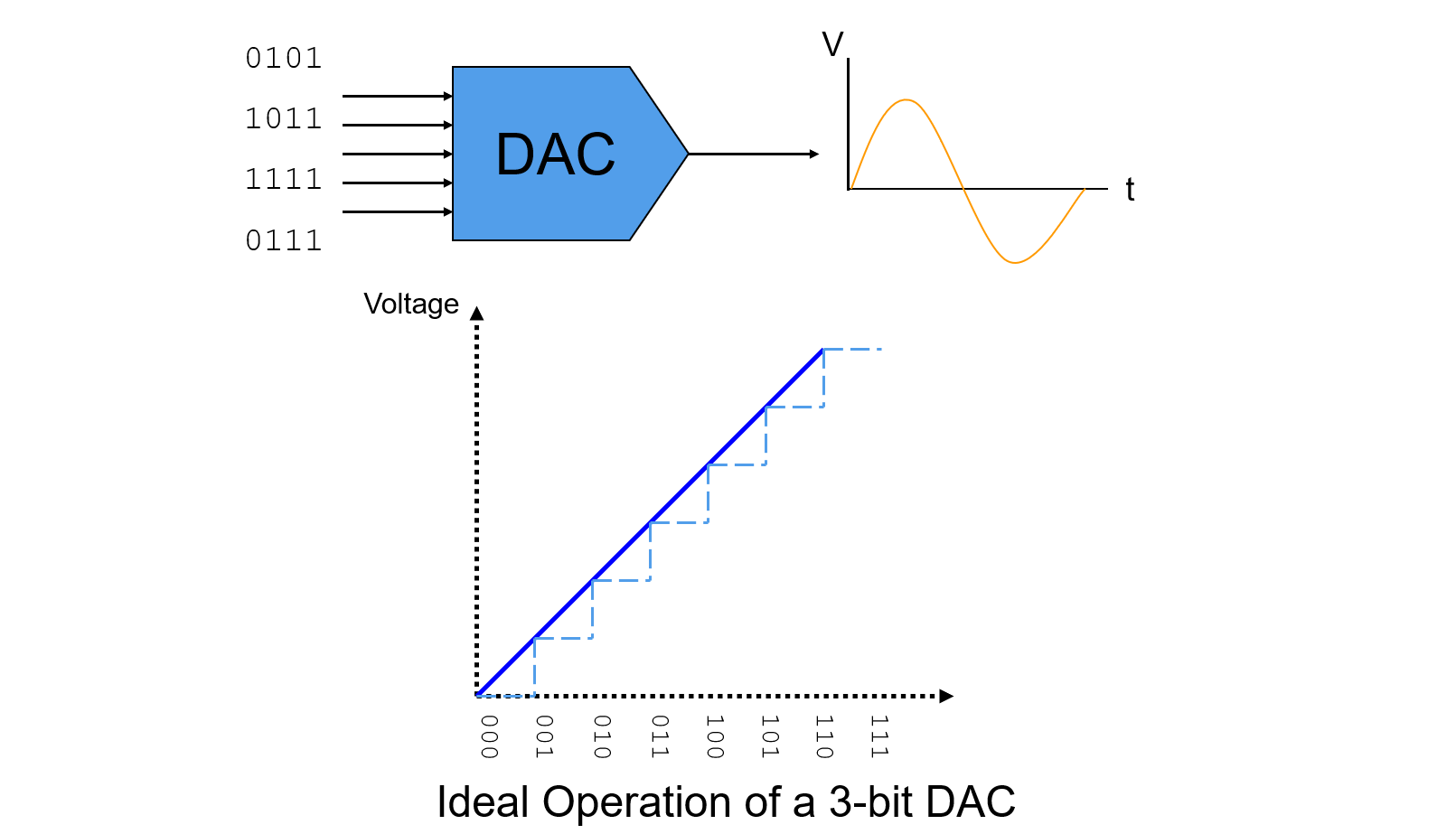
Parámetros Estáticos
Los parámetros estáticos del DAC principalmente incluyen:
- Salida a Escala Cero
- Rango a Escala Completa (REC)
- Tamaño del LSB
- Error de Desplazamiento
- Error de Ganancia
- Error de No Linealidad Diferencial (DNE o DNL)
- Error de No Linealidad Integral (INE o INL)
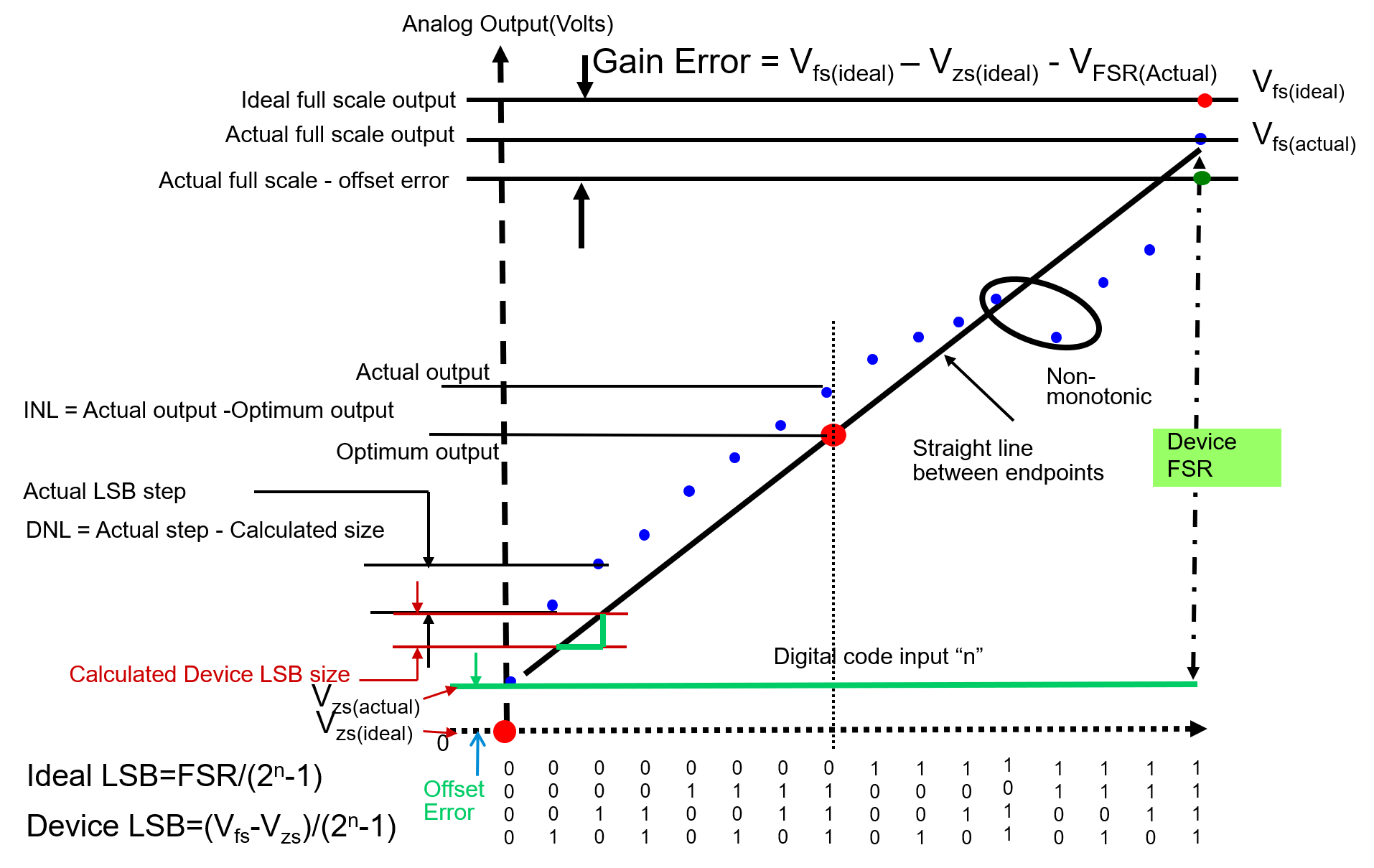
Salida a Escala Cero
La Salida a Escala Cero es el valor de salida medido cuando se presenta el código de entrada digital de nivel cero al dispositivo bajo prueba (DUT).
Rango a Escala Completa (REC)
El rango del voltaje de salida del DAC entre las salidas analógicas mínimas (\(V_{ZS}\)) y máximas (\(V_{FS}\)) se denomina Rango a Escala Completa (REC):
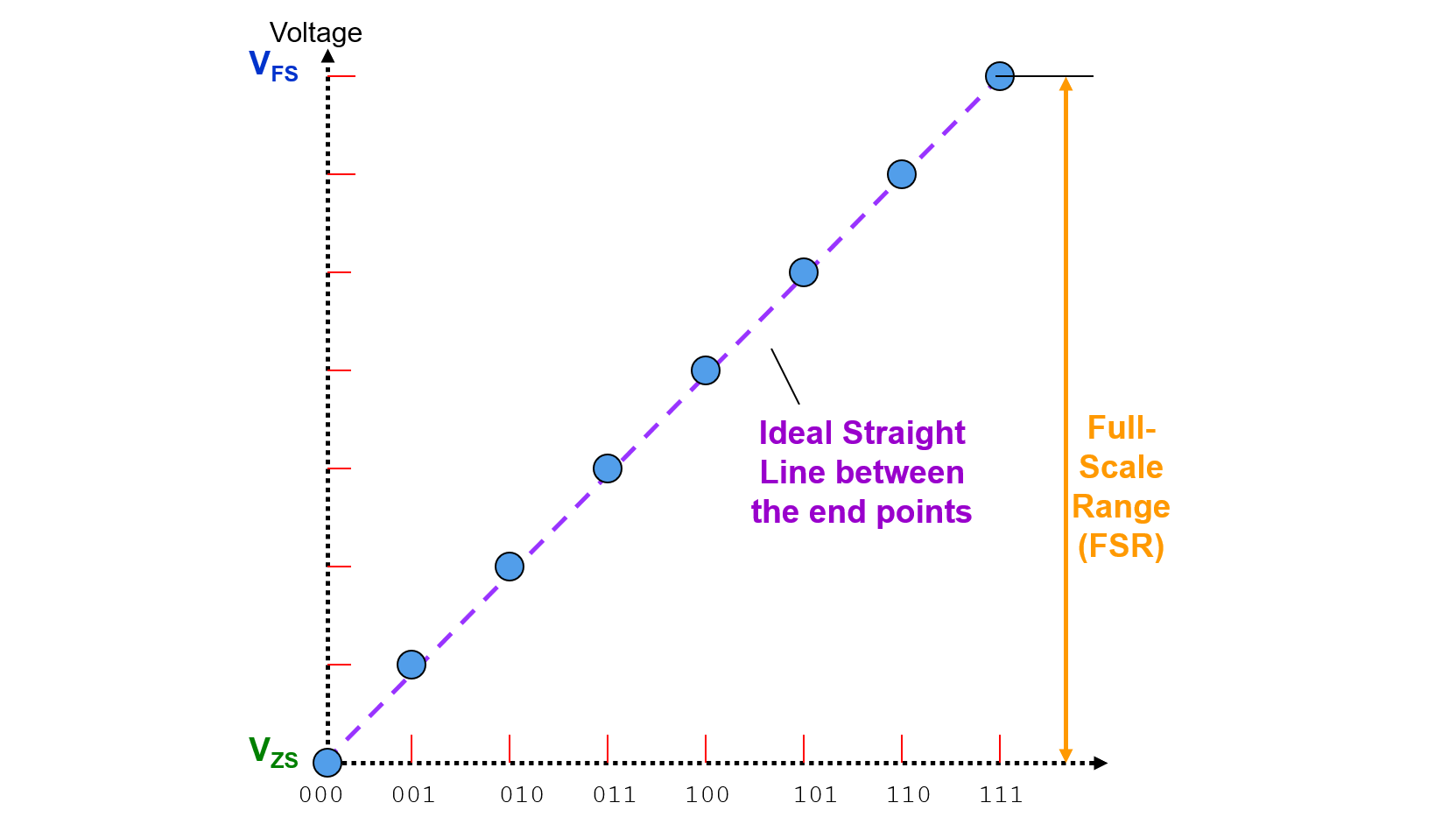
Tamaño del LSB
El cambio promedio en el voltaje entre los códigos de entrada se define como LSB:
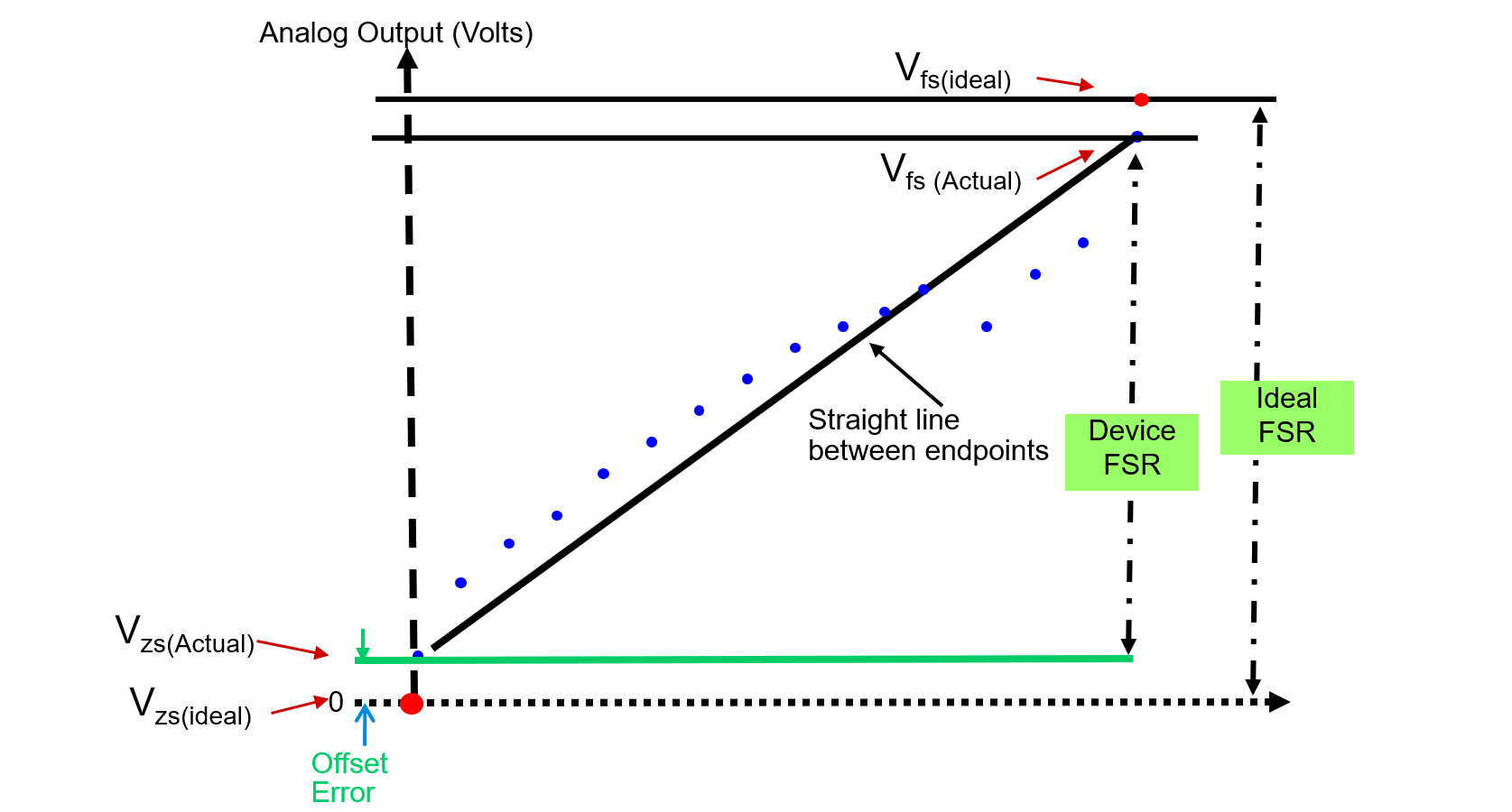
Error de Desplazamiento
El Error de Desplazamiento (Error a Escala Cero) es la diferencia de voltaje entre los puntos de desplazamiento (inicial) ideal y real.
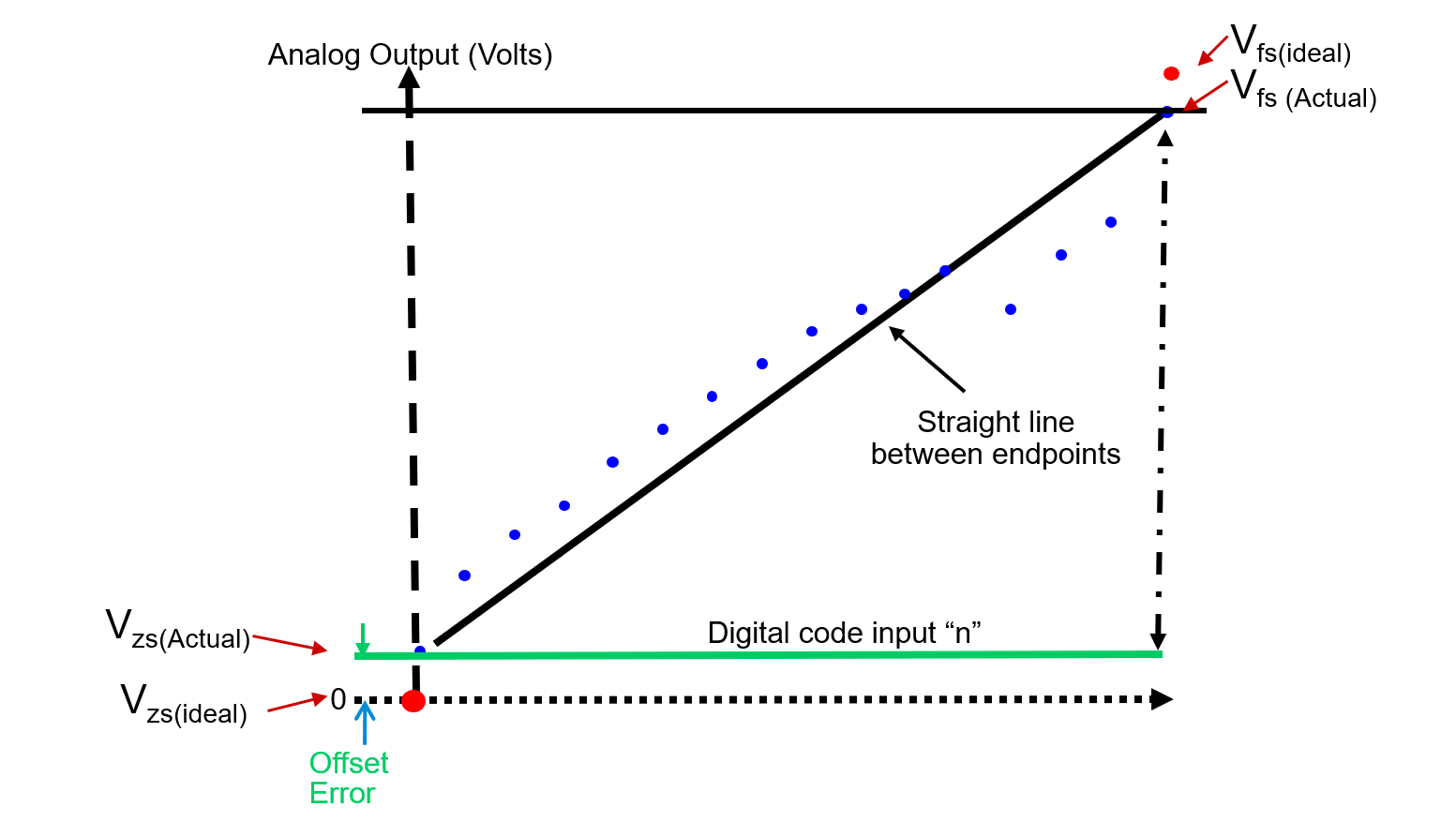
Error de Ganancia
El Error de Ganancia es la diferencia de voltaje entre los puntos de ganancia ideales y reales en la función de transferencia.
Donde
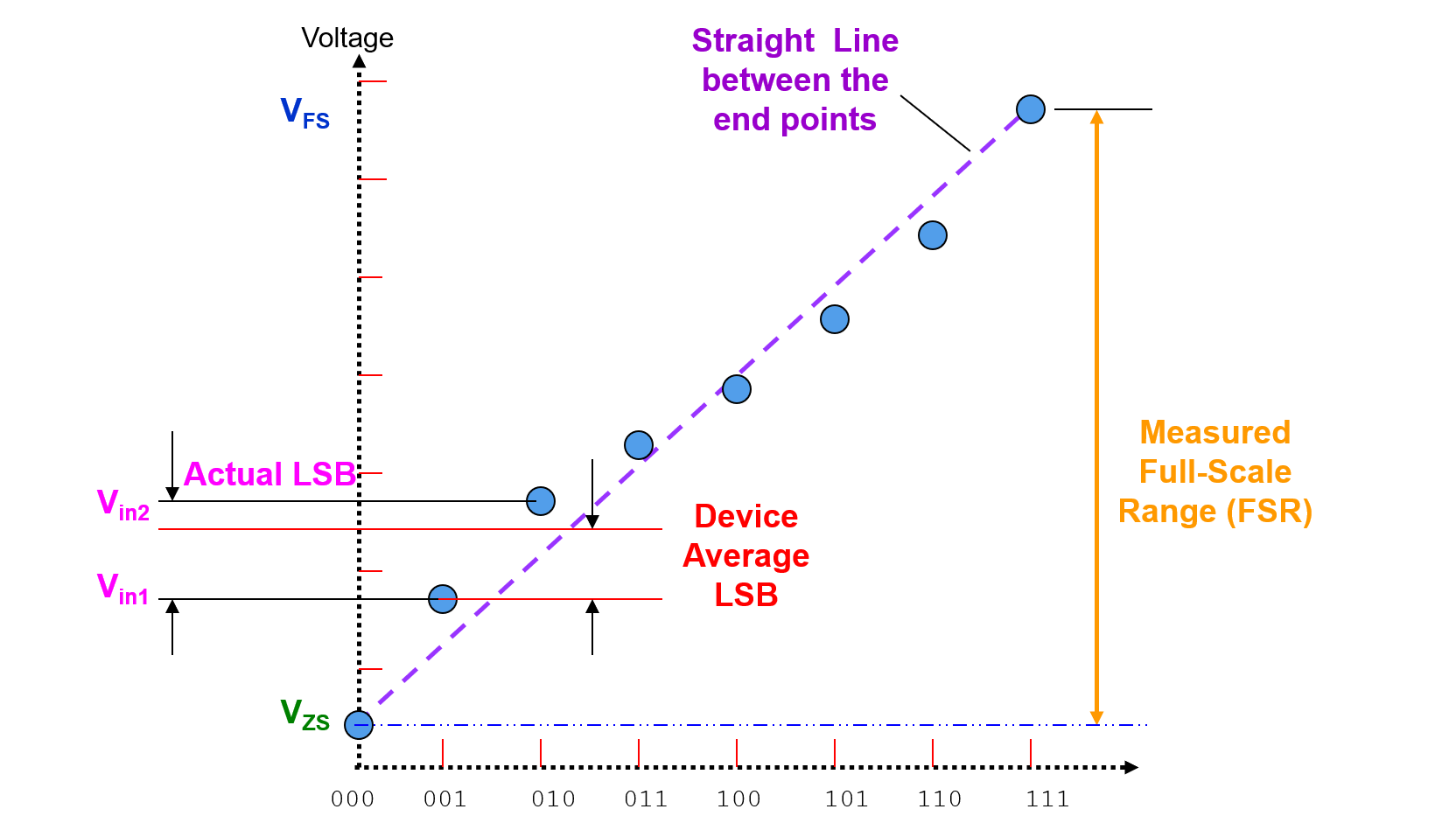
Error de No Linealidad Diferencial (DNL)
El Error de No Linealidad Diferencial (DNL) es la diferencia en el voltaje de salida en un punto específico, en comparación con la salida en el punto de entrada anterior, menos un LSB del dispositivo:
donde \(V_{in2}\) es el voltaje de la transición superior y \(V_{in1}\) es el voltaje de la inferior.
El DNL es una medida del error de linealidad de "señal pequeña". La medición del DNL se realiza de un paso al siguiente, no de cada paso al valor ideal.
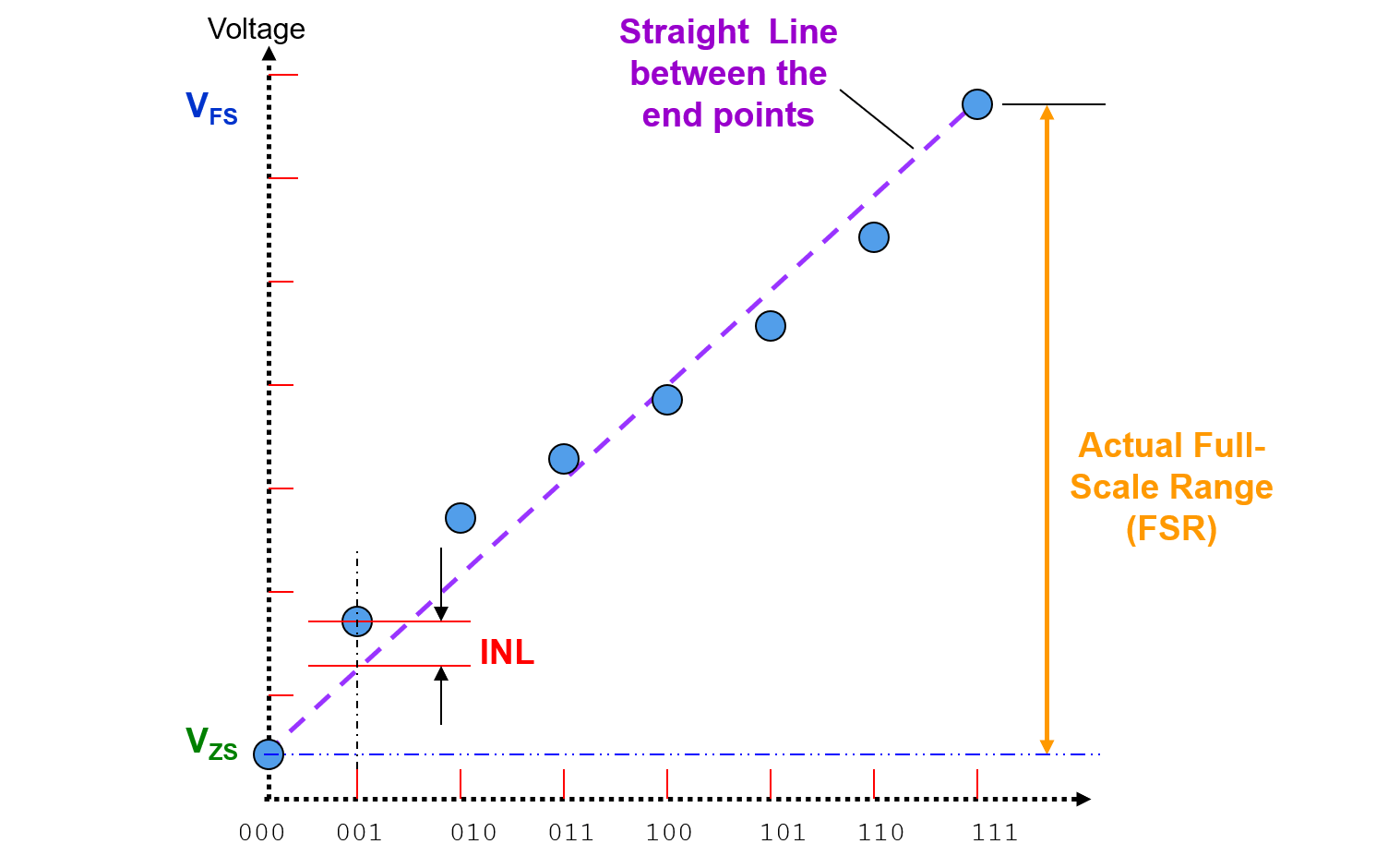
Error de No Linealidad Integral (INL)
El Error de No Linealidad Integral (INL) es el efecto acumulativo de todos los valores de no linealidad diferencial. Es una medida del error de linealidad de "señal grande". El INL en cualquier punto a lo largo de la curva es la desviación de la línea de linealidad ideal.
Además, el INL también se puede expresar como una función del DNL:
Cómo Probar Parámetros Estáticos
Configuración del Sistema de Pruebas
Configuración del sistema de pruebas para las pruebas de parámetros estáticos del DAC:
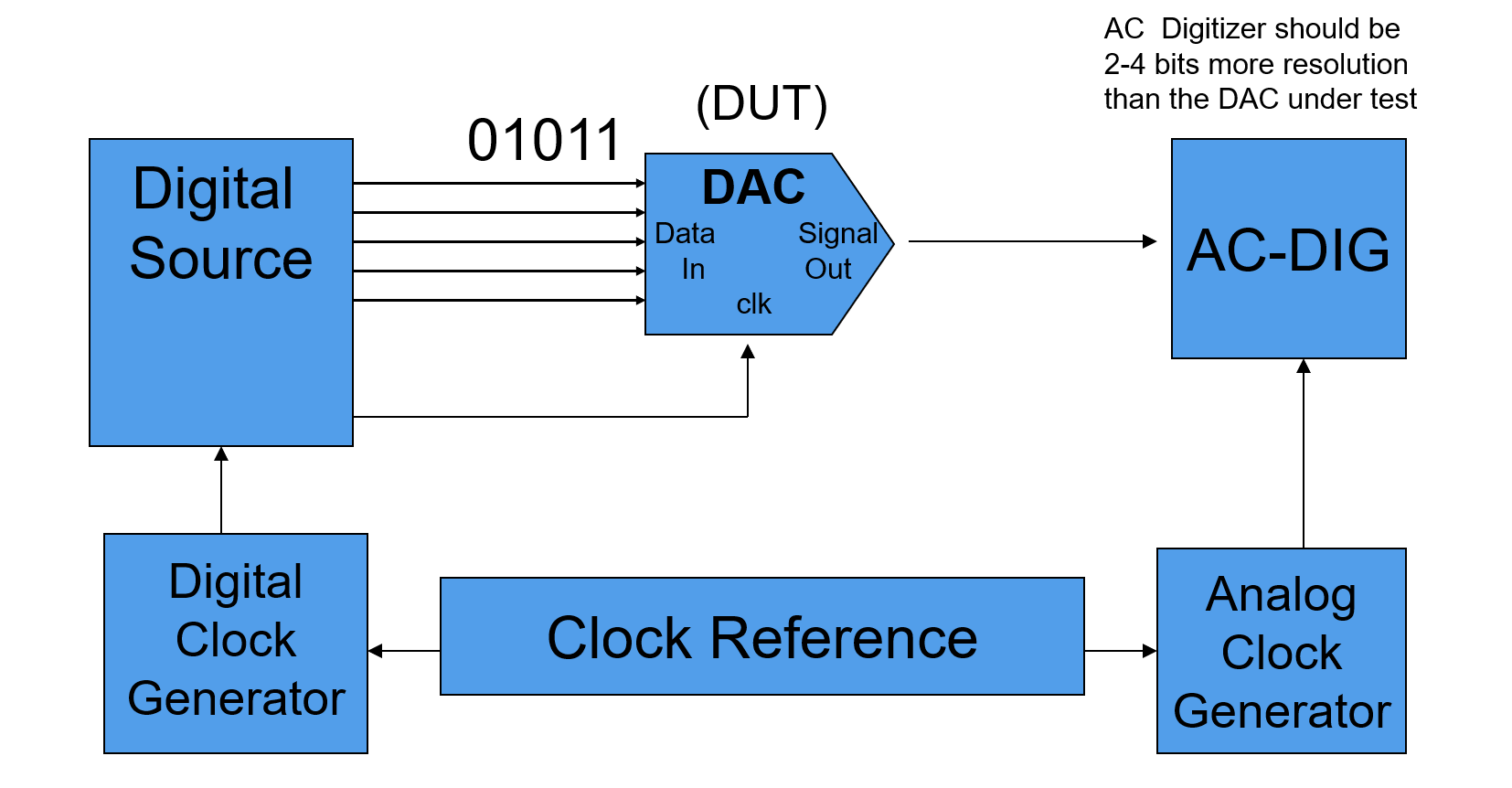
Diagrama de bloque de la configuración de la señal:
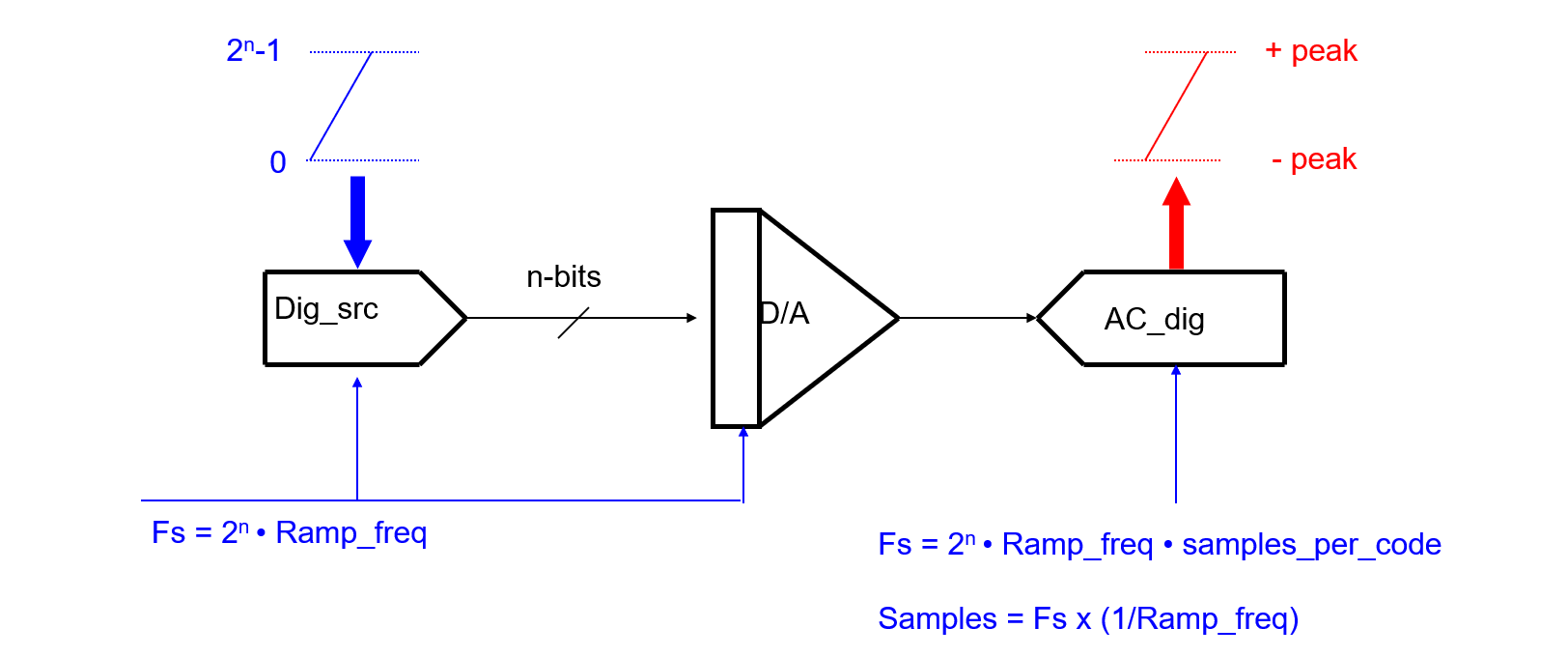
Concepto de Pruebas
El procedimiento para probar los parámetros estáticos de un DAC DUT se describe a continuación.
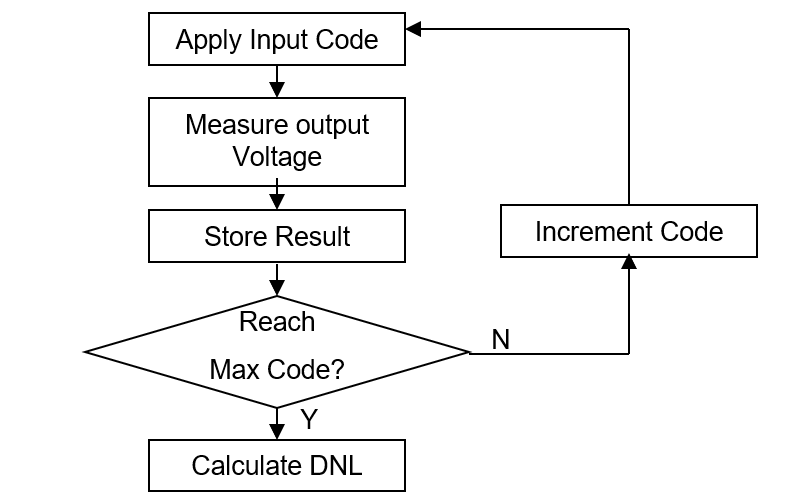
1. Medir el voltaje de salida aplicando las entradas de datos digitales desde Cero Escala hasta Escala Completa

2. Calcular el DNL para cada código de entrada
$$
DNL[i]=\frac{SalidaMedida[i]-SalidaMedida[i-1]-LSB_{promedio}}{LSB_{promedio}}
$$
Donde
$$
LSB_{promedio}=\frac{SalidaMedida[n]-SalidaMedida[0]}{2^{bits}-1}
$$
#### 3. Obtener el DNL máximo y mínimo
#### 4. Calcular el INL para cada paso
#### 5. Obtener el INL máximo y mínimo
## Referencias y Agradecimientos
- _Fundamentos de Pruebas Utilizando ATE_
- _Los Fundamentos de las Pruebas de Señal Mixta de Brian Lowe_
> Original: <https://wiki-power.com/>
> Este artículo está protegido por un acuerdo [CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by/4.0/deed.en), y debe ser reproducido con atribución.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.