Fundamentos de la Prueba de Señales Mixtas
Las señales mixtas contienen tanto señales analógicas como digitales. Los dispositivos que procesan señales mixtas típicamente incluyen ADCs, DACs, interruptores analógicos y multiplexores, amplificadores de muestra y retención, entre otros.
Como parte de esto, las señales analógicas son señales que utilizamos en el mundo real, como voz o temperatura; son continuas en cuanto a tiempo y amplitud. Para procesar señales analógicas en computadoras, necesitamos convertirlas en señales digitales, ya que son discretas tanto en tiempo como en amplitud.
Teoría del Muestreo
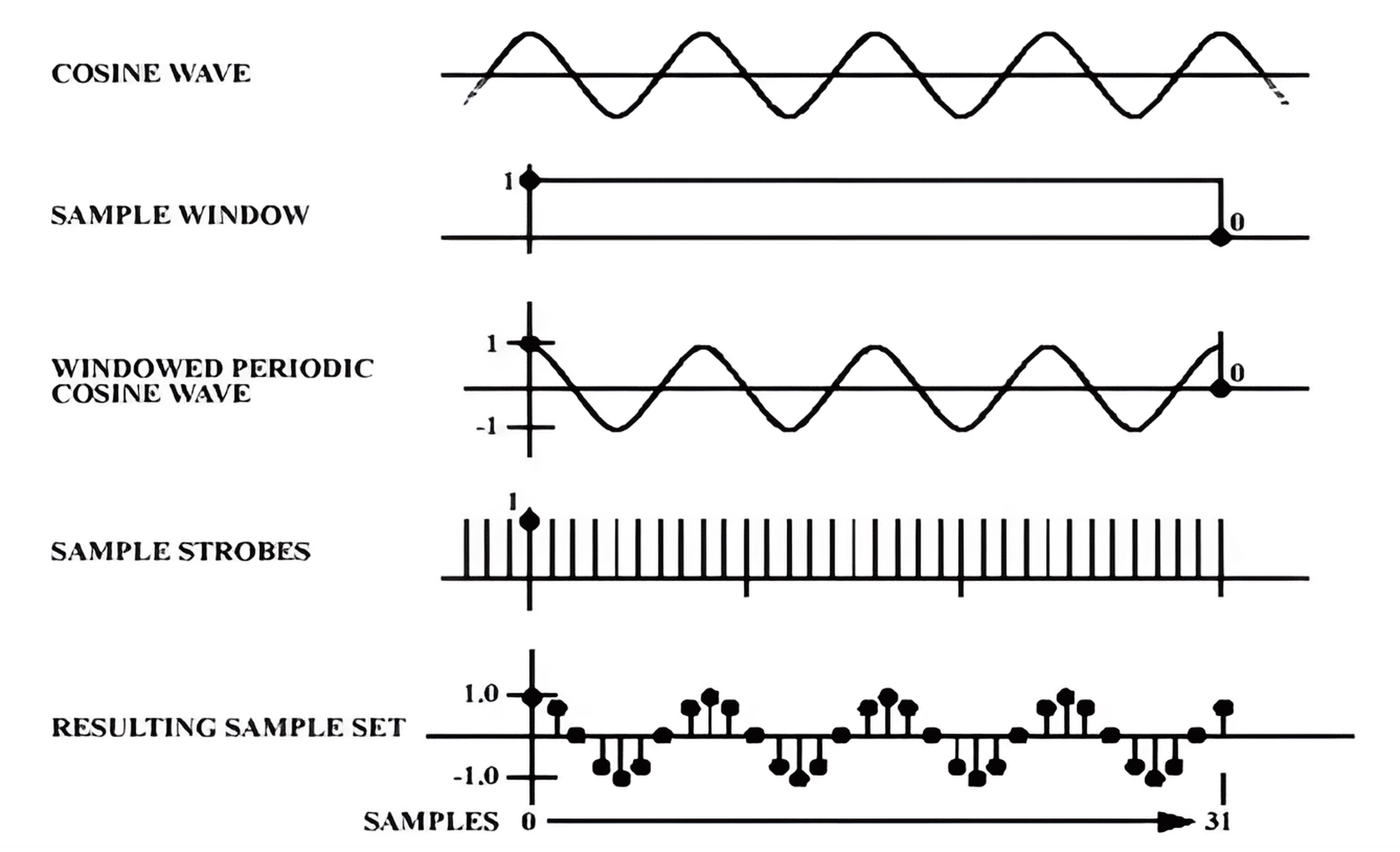
La teoría del muestreo se aplica cuando la señal es periódica, o de lo contrario se introducirán errores.
Teorema de Nyquist
Utilizamos el Teorema de Nyquist para obtener la frecuencia mínima de muestreo al muestrear señales:
Debemos muestrear a una velocidad superior al doble de la frecuencia más alta de interés para poder recrear una señal a partir de sus muestras y evitar la pérdida de información.
Si muestreamos a una frecuencia inferior a la tasa de Nyquist, se producirá un fenómeno llamado aliasing (componentes no deseadas) cuando intentemos convertirla de nuevo en una señal continua en el tiempo, y algunas de las frecuencias en la señal original pueden perderse.
Para minimizar el problema de aliasing, necesitamos eliminar las frecuencias superiores a \(\frac{F_s}{2}\) de la señal, a través de un filtro antialiasing (por ejemplo, un filtro pasa bajos):
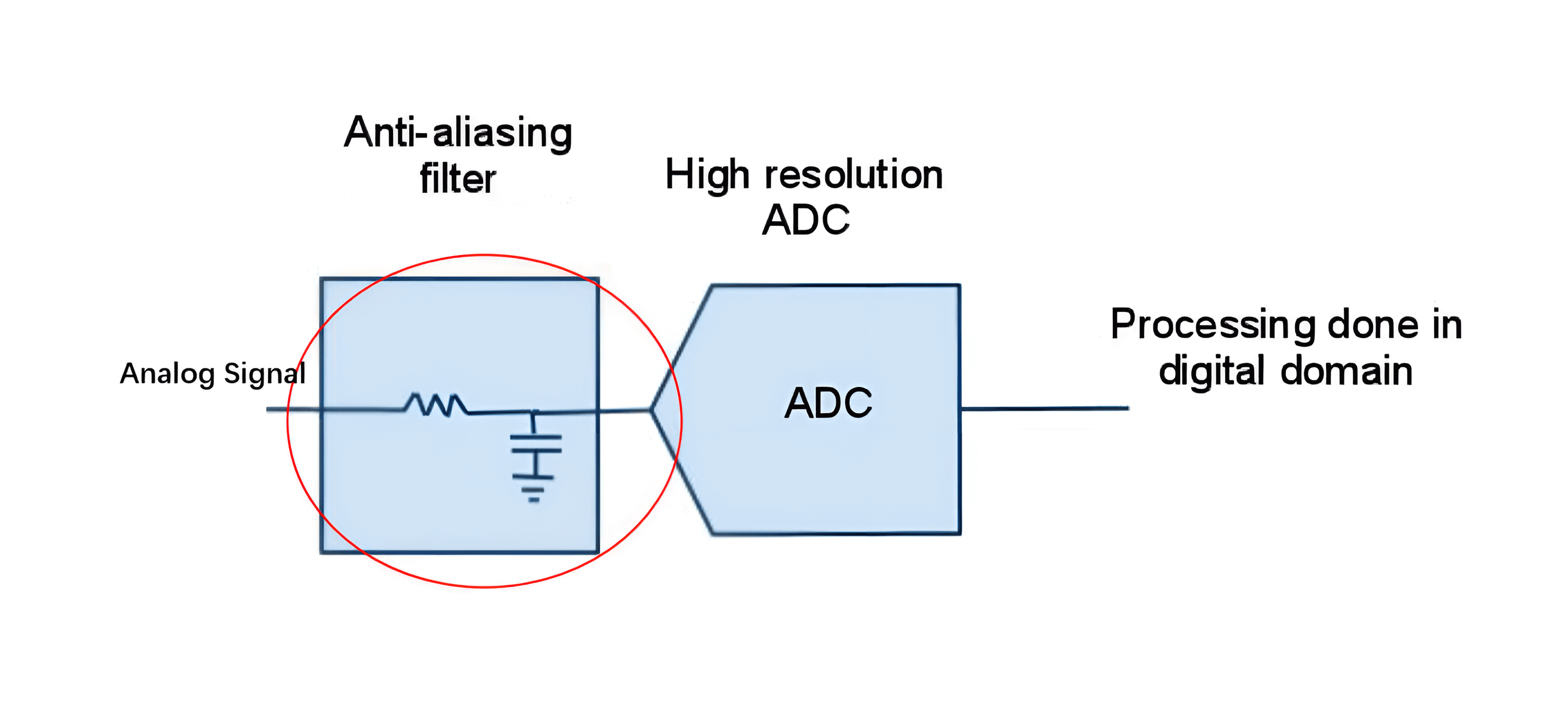
Muestreo Coherente
Si un conjunto de muestras de tiempo no contiene un número entero preciso de ciclos, se producirá una fuga espectral.
Muestreo coherente es asegurar la continuidad del muestreo y prevenir la fuga espectral, garantiza que un conjunto de muestras (una serie de muestras que representan la señal analógica) tenga una relación fija y bien definida entre la frecuencia de muestreo \(F_s\), el número de muestras \(N\), la frecuencia de la señal de prueba \(F_i\) y el número de periodos de señal de prueba muestreados \(M\):
El tiempo total requerido para tomar todas las muestras se llama el Período de Prueba Unitario (UTP) y requiere \(M\) ciclos de la señal de prueba, que tiene una frecuencia de \(F_i\).
Por ejemplo, si deseamos calcular la \(F_s\) de una onda senoidal continua repetitiva, donde \(F_i\) es 1 kHz, \(M=3\) y $N=16`:
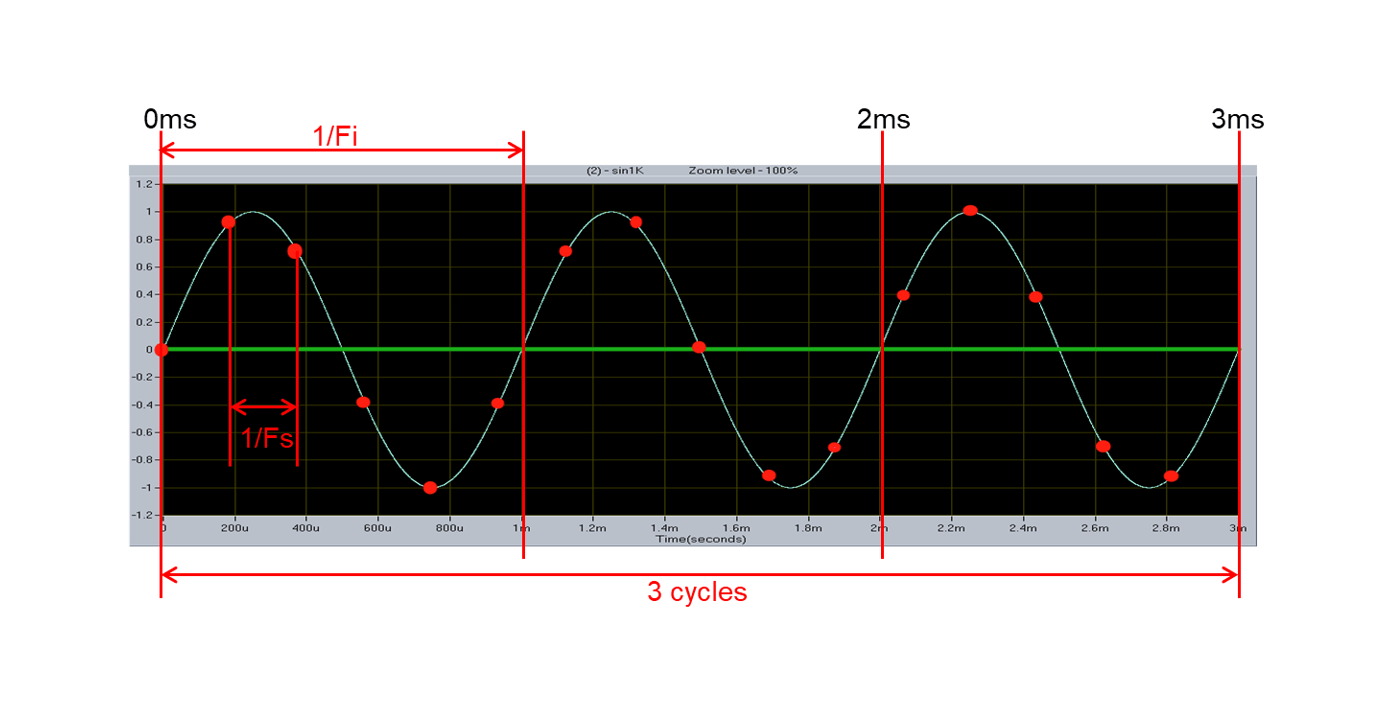
Por lo tanto, podemos concluir que $F_s=5.333 kHz`.
Consejos importantes sobre el muestreo coherente:
- Aumentar $M
y/o $Naumentará tanto la precisión como el tiempo de prueba. - $M
y $Ndeben ser números enteros. - $N` debe ser una potencia de 2 al utilizar la Transformada Rápida de Fourier (FFT).
- Se recomienda que $M
y $Nsean mutuamente primos para que cada muestra proporcione información única. Esto se describe a continuación.
Si \(My $N no son mutuamente primos (\)M=3, N=12`), las muestras se toman en la misma posición en cada ciclo, por lo que no hay información nueva:
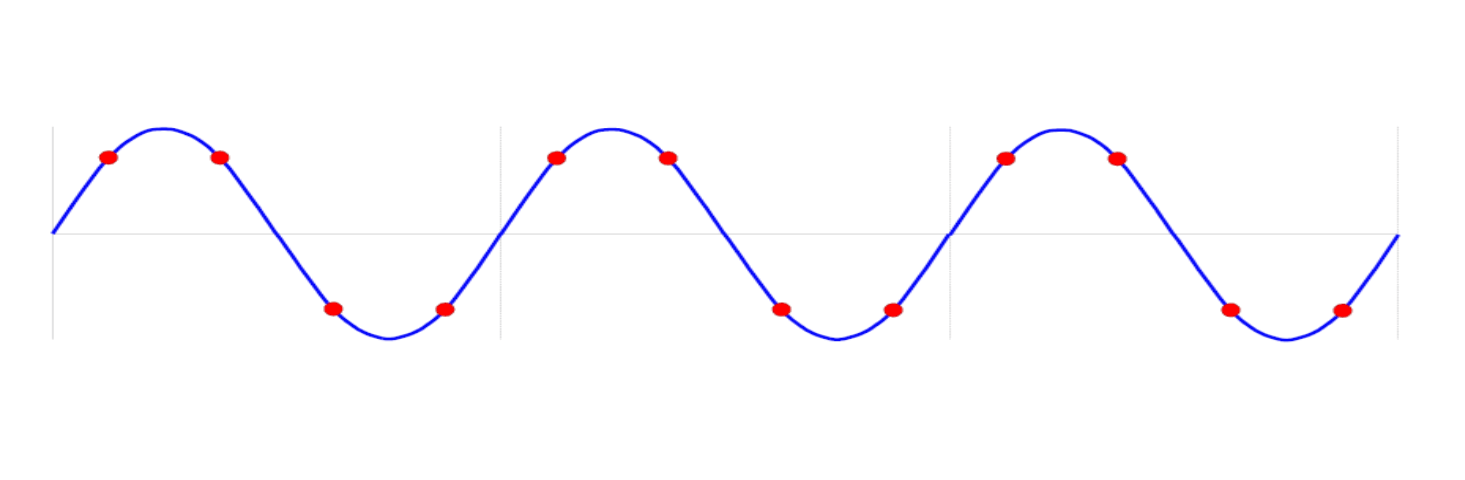
Si \(My $N son mutuamente primos (\)M=3, N=16`), entonces son mutuamente primos y cada muestra es discreta, por lo que proporciona información única:
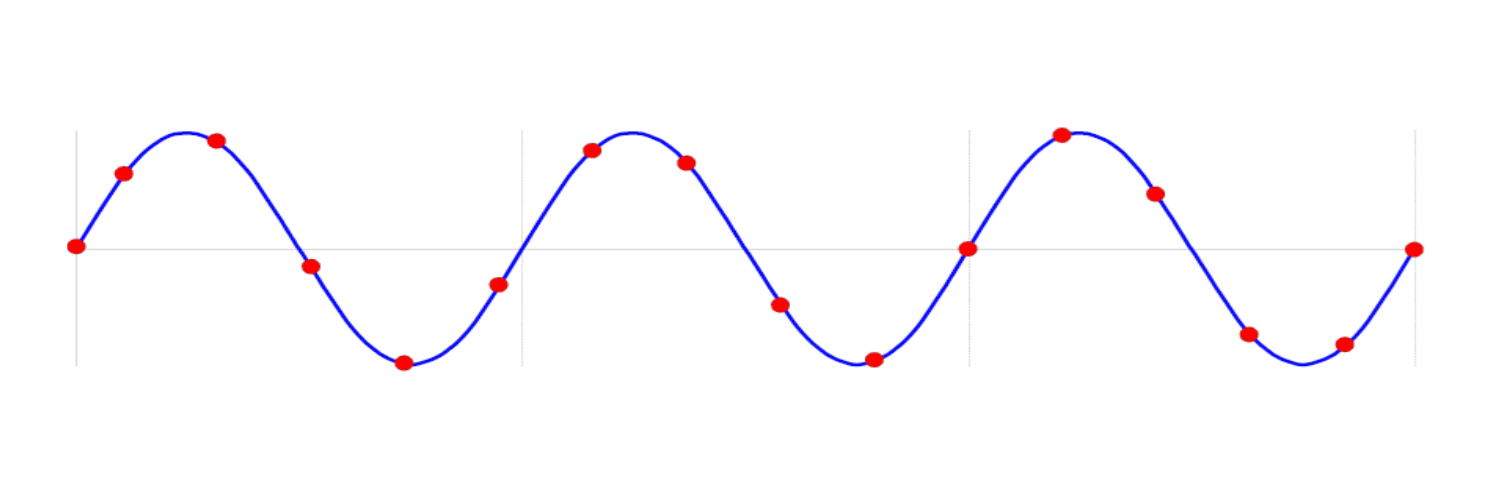
Algoritmos Comunes de Análisis de Frecuencia
Para \(N\) muestras de una señal en el dominio del tiempo, existen \(N\) valores de la señal en el dominio de la frecuencia, y \(N/2\) valores del espectro de potencia en el dominio de la frecuencia. A continuación, se muestra un ejemplo típico de componentes espectrales:
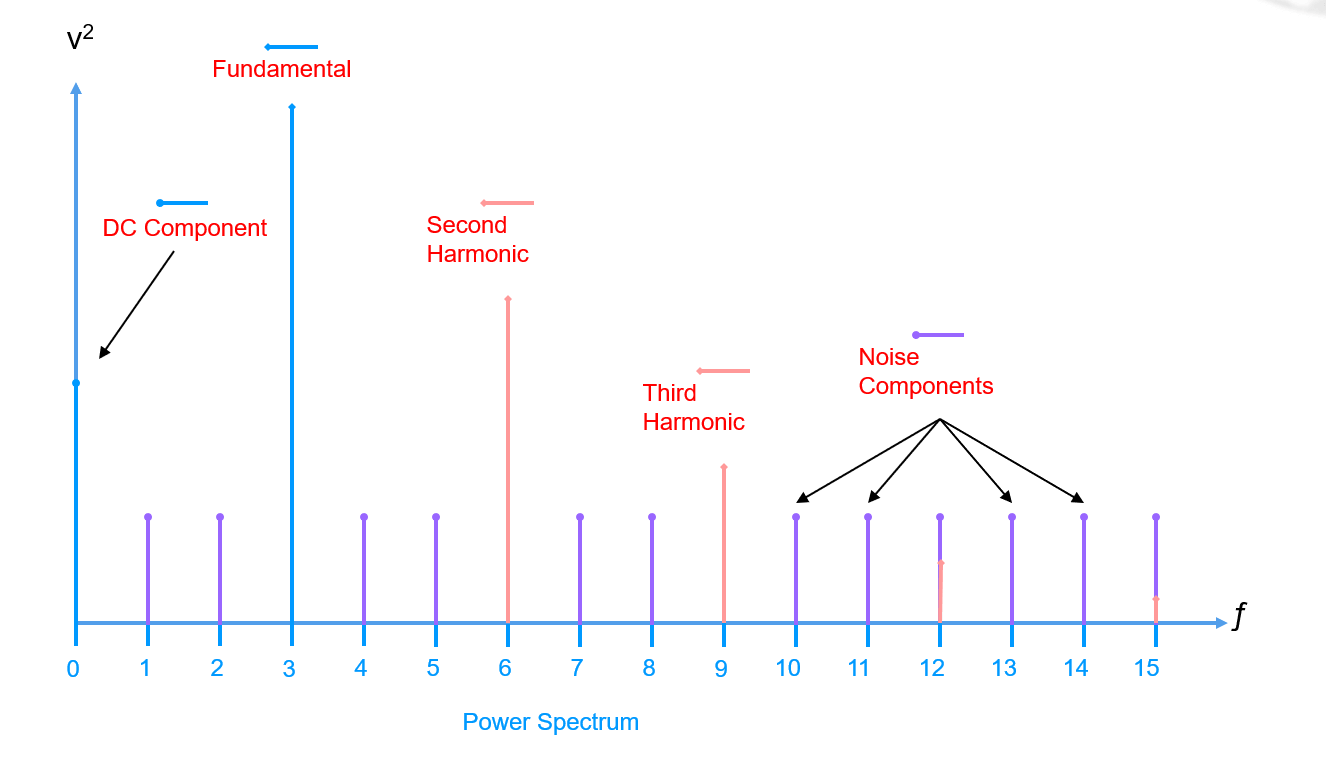
Existen varios parámetros para describir componentes espectrales de la siguiente manera:
- Relación Señal a Ruido (SNR)
- Distorsión Armónica Total (THD)
- Relación Señal a Ruido y Distorsión (SINAD)
- Distorsión de Intermodulación (IM)
- Rango Dinámico Libre de Espurias (SFDR)
Relación Señal a Ruido (SNR)
La Relación Señal a Ruido (SNR) se deriva almacenando primero el valor del fundamental (potencia de la señal):
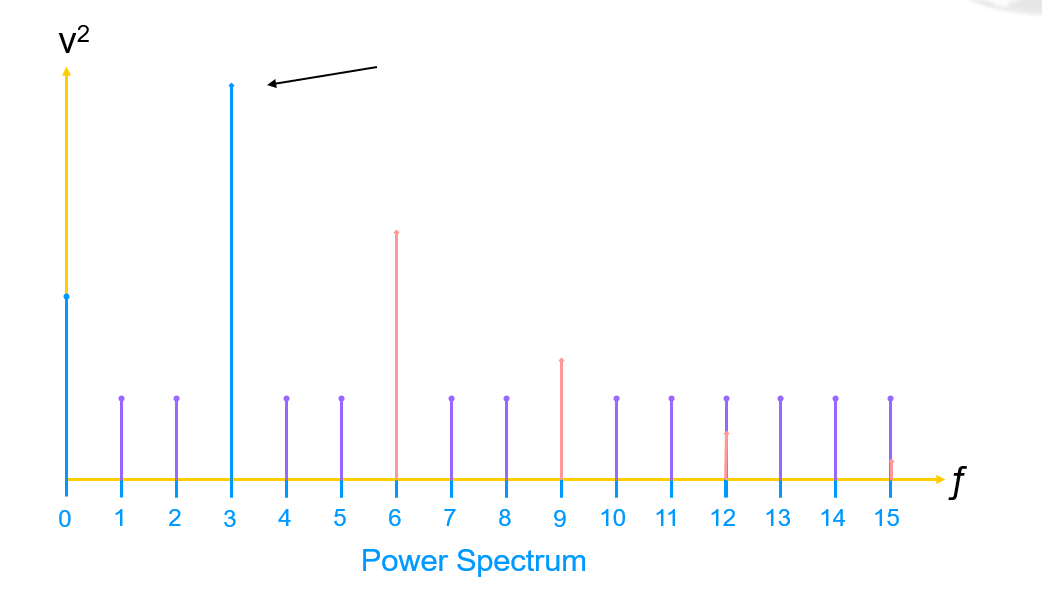
Luego, se elimina el componente de corriente continua y las armónicas (generalmente hasta la quinta armónica):
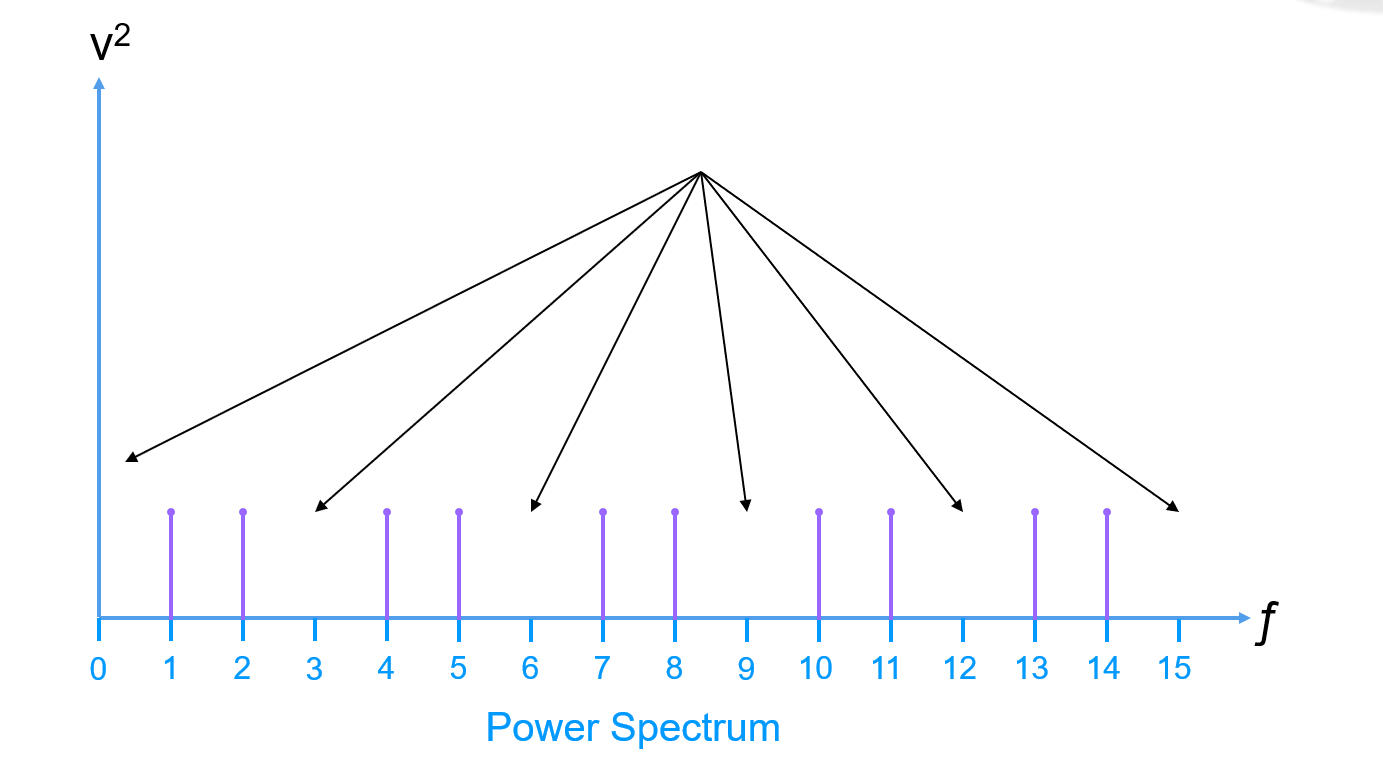
A continuación, se suman todos los valores del espectro de potencia restantes (la potencia del ruido) medida mediante el valor RMS (Raíz Cuadrada de la Media, el voltaje analógico que es igual a un voltaje de corriente continua que contiene la misma cantidad de energía; para una onda senoidal, el valor RMS es 0.707 veces el valor pico):
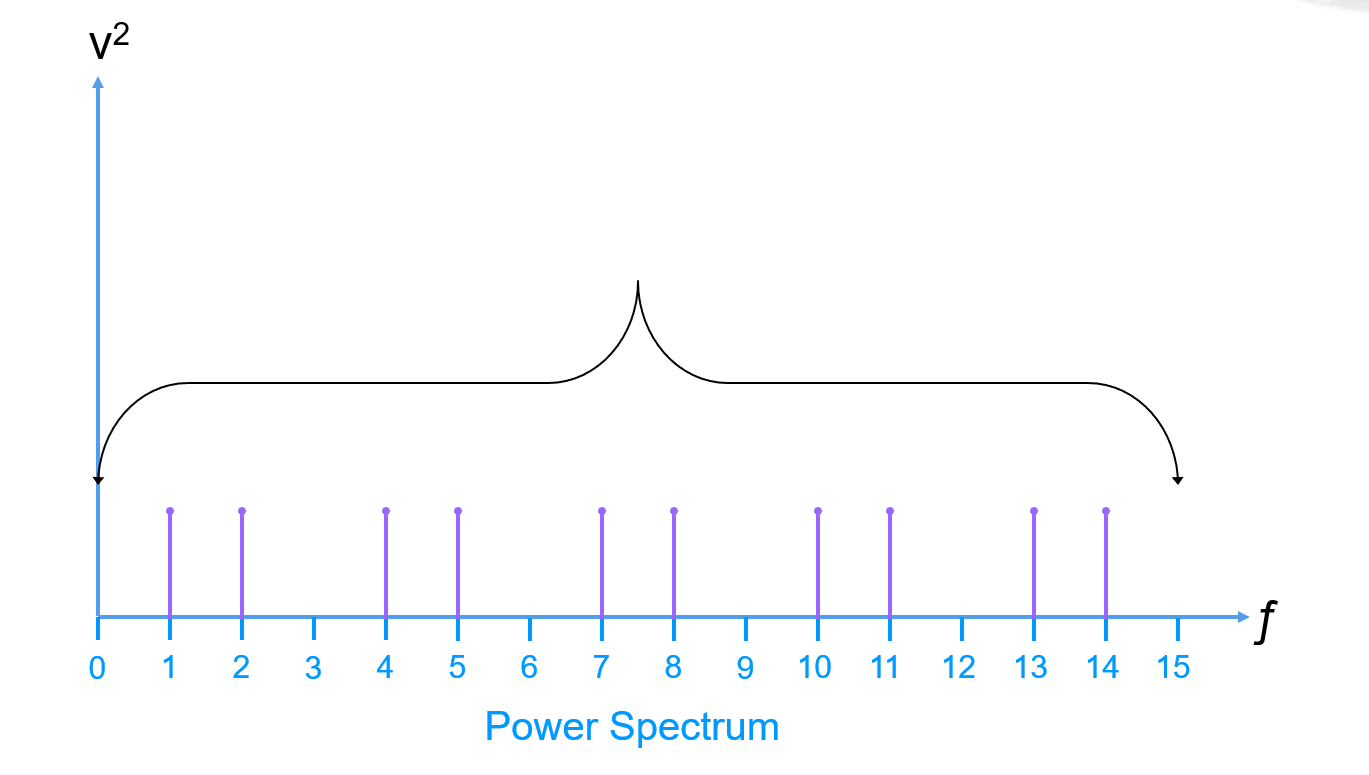
Finalmente, podemos concluir que:
El SNR se expresa generalmente en decibeles (dB) y suele ser un valor positivo (asumiendo que la Potencia del Fundamental es mucho mayor que la Potencia del Ruido).
Distorsión Armónica Total (THD)
La Distorsión Armónica Total (THD) se deriva manteniendo una suma acumulativa de la potencia armónica total (generalmente solo las primeras cinco armónicas, comenzando en la segunda armónica):
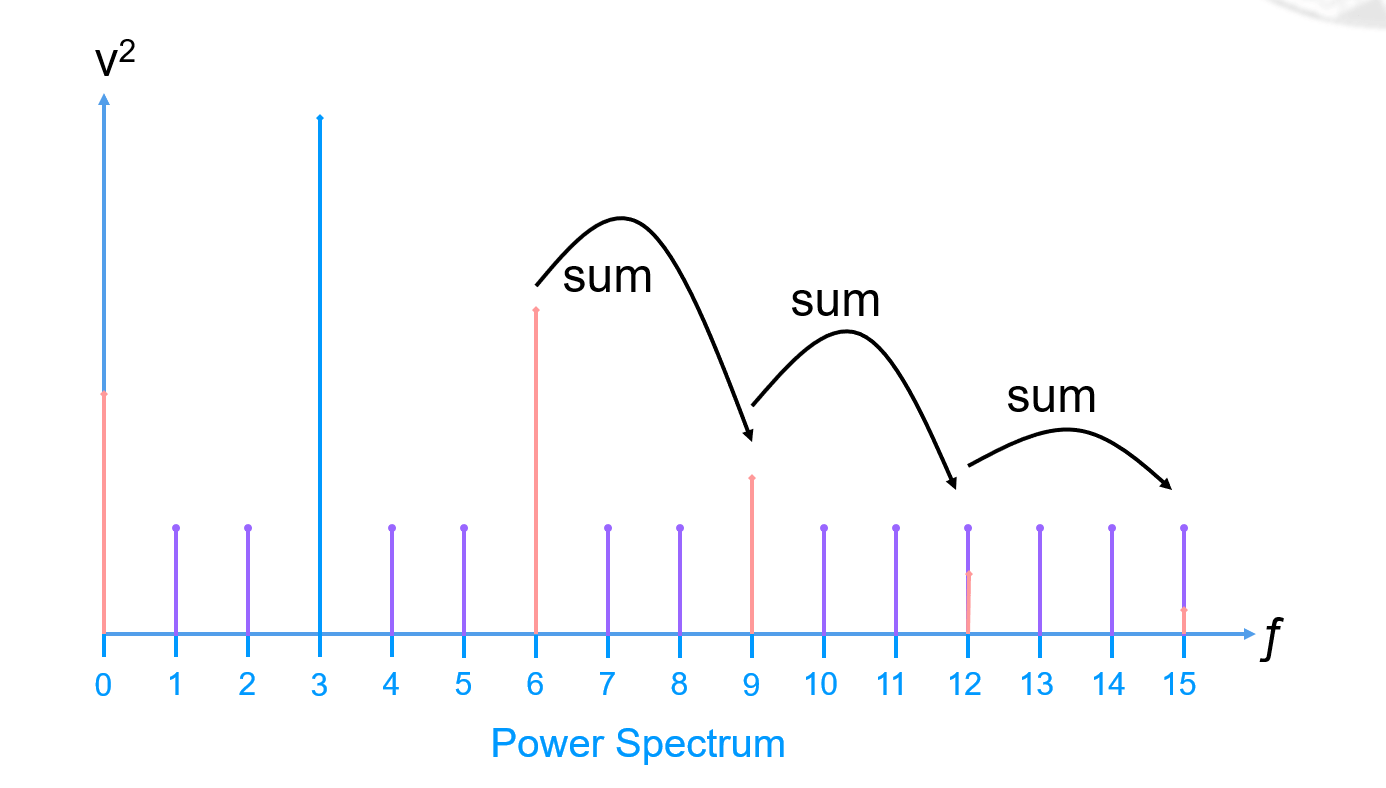
Y podemos concluir que:
THD suele ser un valor negativo (asumiendo que la Potencia Fundamental es mucho mayor que la Potencia Total Armónica).
Relación Señal-Ruido y Distorsión (SINAD)
La Relación Señal-Ruido y Distorsión (SINAD) sigue la misma metodología que el cálculo de SNR, pero ahora se añade la potencia de las armónicas y se elimina solo el componente de corriente continua (DC).
Y podemos concluir que:
Distorsión de Intermodulación (IM)
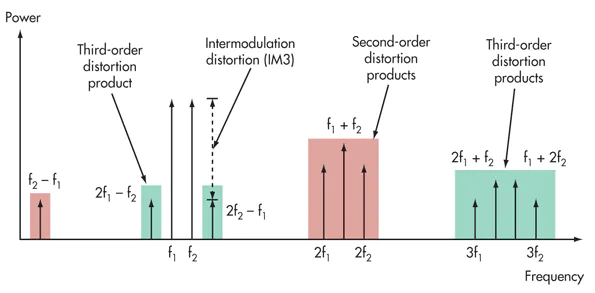
La Distorsión de Intermodulación (IM) ocurre cuando dos o más señales se utilizan en un sistema no lineal. El espectro no solo consistirá en las señales originales, sino que también contendrá la suma y la diferencia de las señales de entrada junto con sus armónicas.
Rango Dinámico Libre de Espurias (SFRD)
El Rango Dinámico Libre de Espurias (SFRD) se obtiene encontrando el elemento más alto después del fundamental (ignorando el componente de corriente continua):
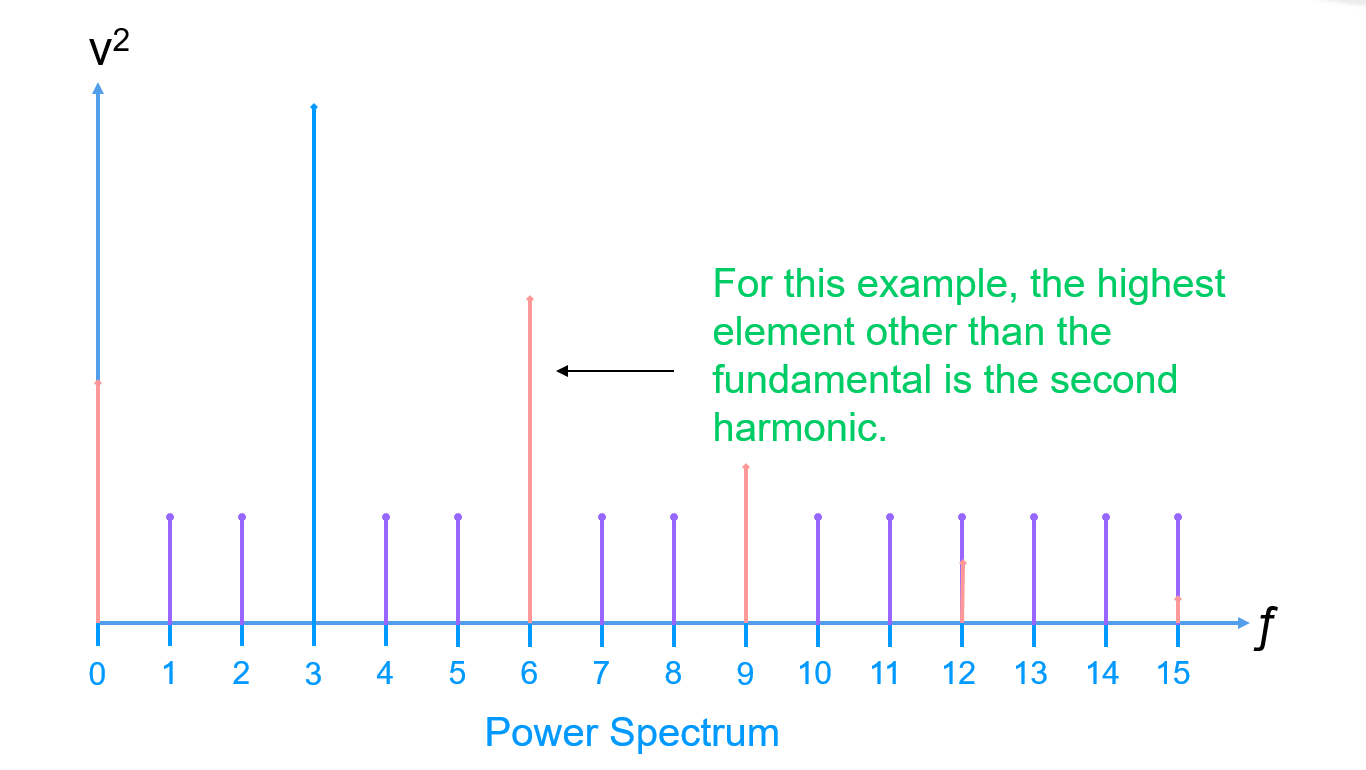
Tenga en cuenta que el elemento más alto puede o no ser un armónico. Por lo tanto, podemos concluir que:
El Rango Dinámico Libre de Espurias es un valor positivo (asumiendo que la Potencia Fundamental es mucho mayor que la Potencia de la Siguiente Espuria más Alta).
Arquitectura del Probador de Señal Mixta Genérica
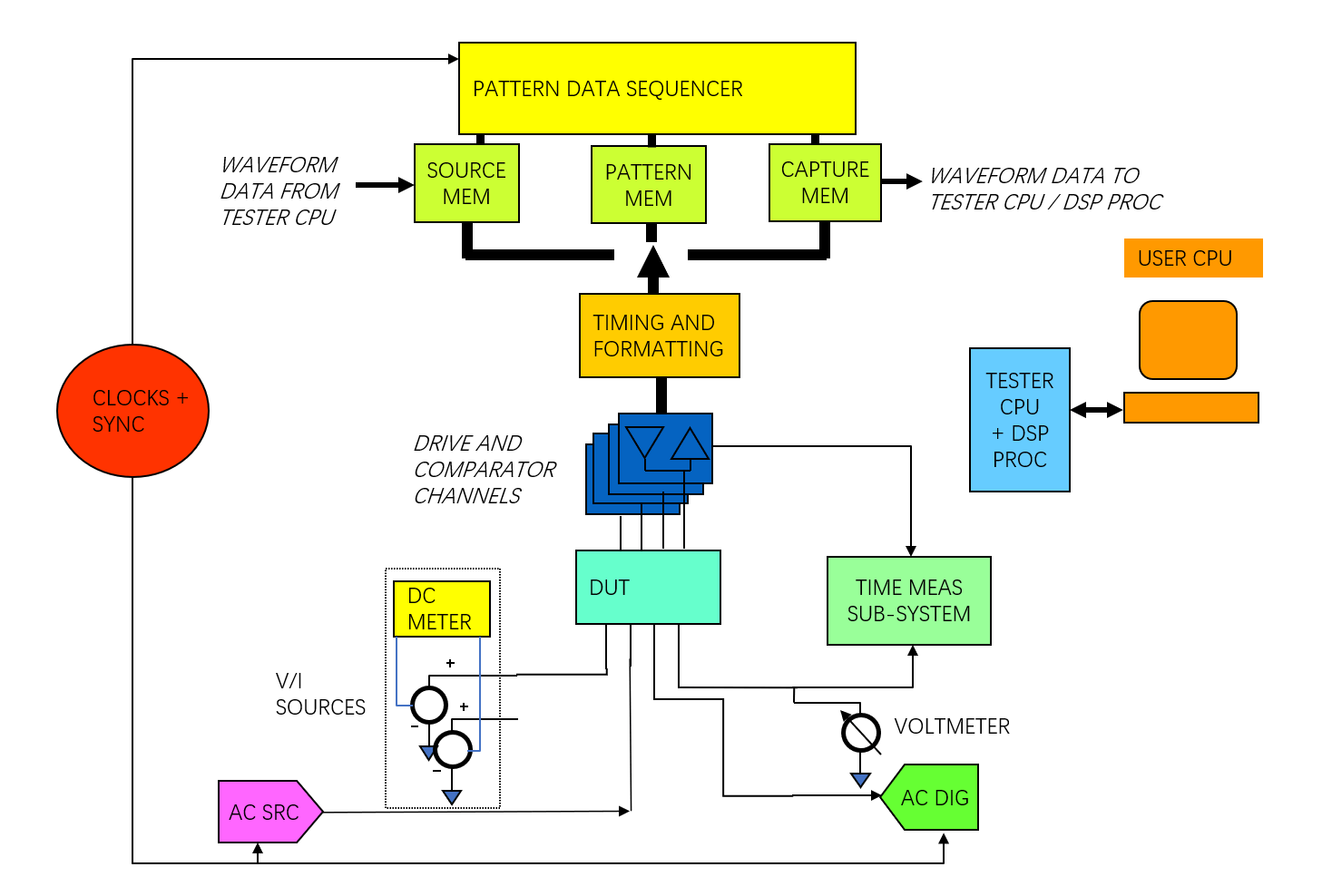
En el probador de señal mixta genérica, el Generador de Señales Arbitrarias (AWG, fuente de CA) y el Digitalizador de Señales (WD, digitalización de CA) están ambos conectados al Dispositivo Bajo Prueba (DUT) a través de interconexiones de relé a través de la placa de canal.
Generador de Formas de Onda Arbitrarias (AWG)
El Generador de Formas de Onda Arbitrarias (AWG) es un generador de señales de baja distorsión. Contiene un Convertidor Analógico-Digital (DAC) para generar una señal analógica a partir de datos digitales.
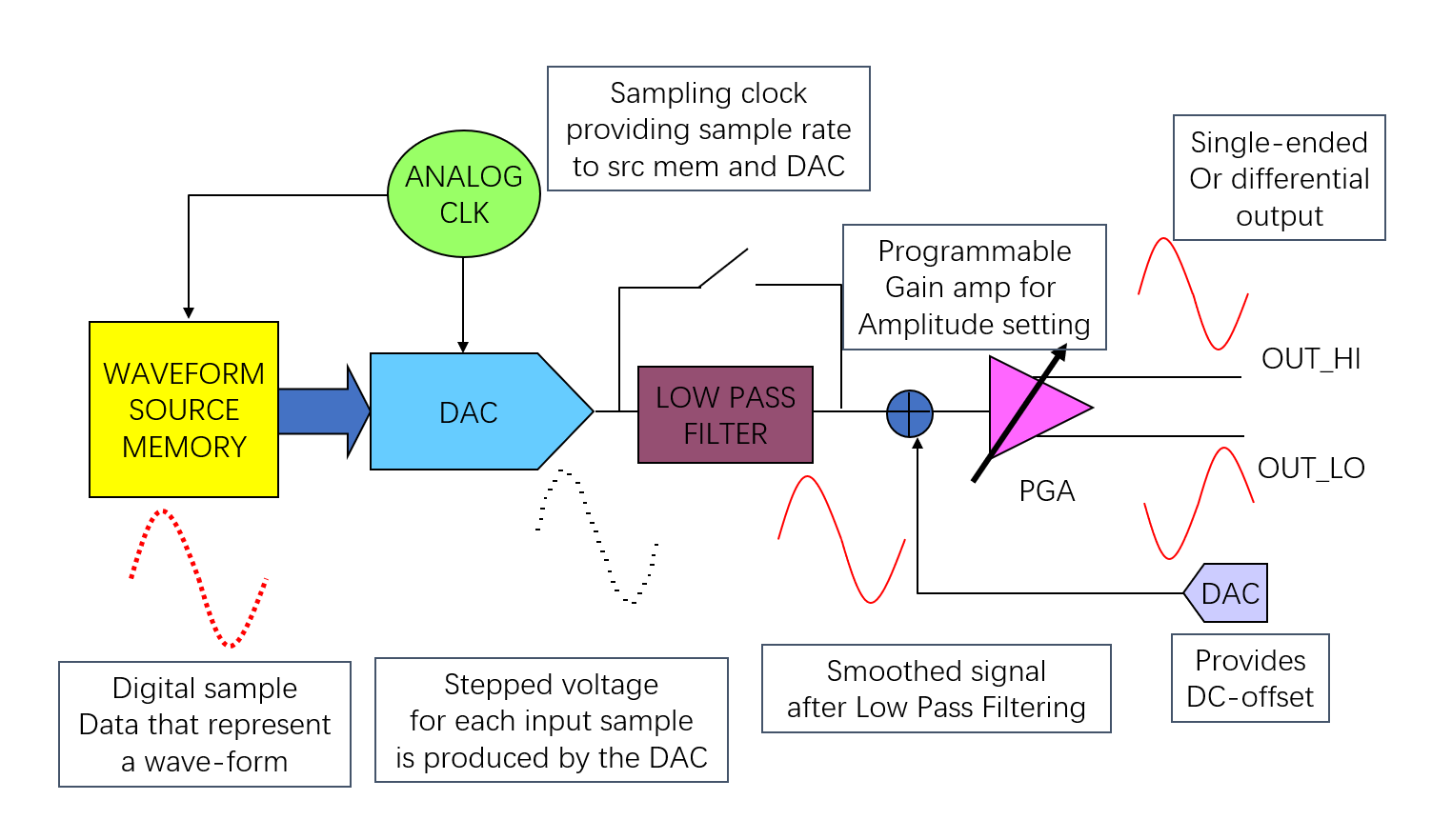
El Filtro Paso Bajo (LPF) se utiliza para suavizar la forma de onda y eliminar componentes de alta frecuencia. Un conjunto de puntos de datos para una forma de onda dada se almacena en la memoria de origen de la forma de onda, y cada vez que se produce un pulso de reloj, un punto de datos se envía al DAC.
Parámetros importantes del AWG:
- Salida de Voltaje Pico a Pico Máximo
- Resolución de la Forma de Onda (Resolución del DAC)
- Ancho de Banda
- Profundidad de Memoria de Origen de la Forma de Onda
- Impedancia de Salida
- Ruido, THD, SNR
Digitalizador de Formas de Onda (WD)
El Digitalizador de Formas de Onda (WD) muestrea señales analógicas y las convierte en valores digitales. Realiza la operación opuesta al AWG. Convierte señales analógicas en muestras digitales que representan la señal analógica original.
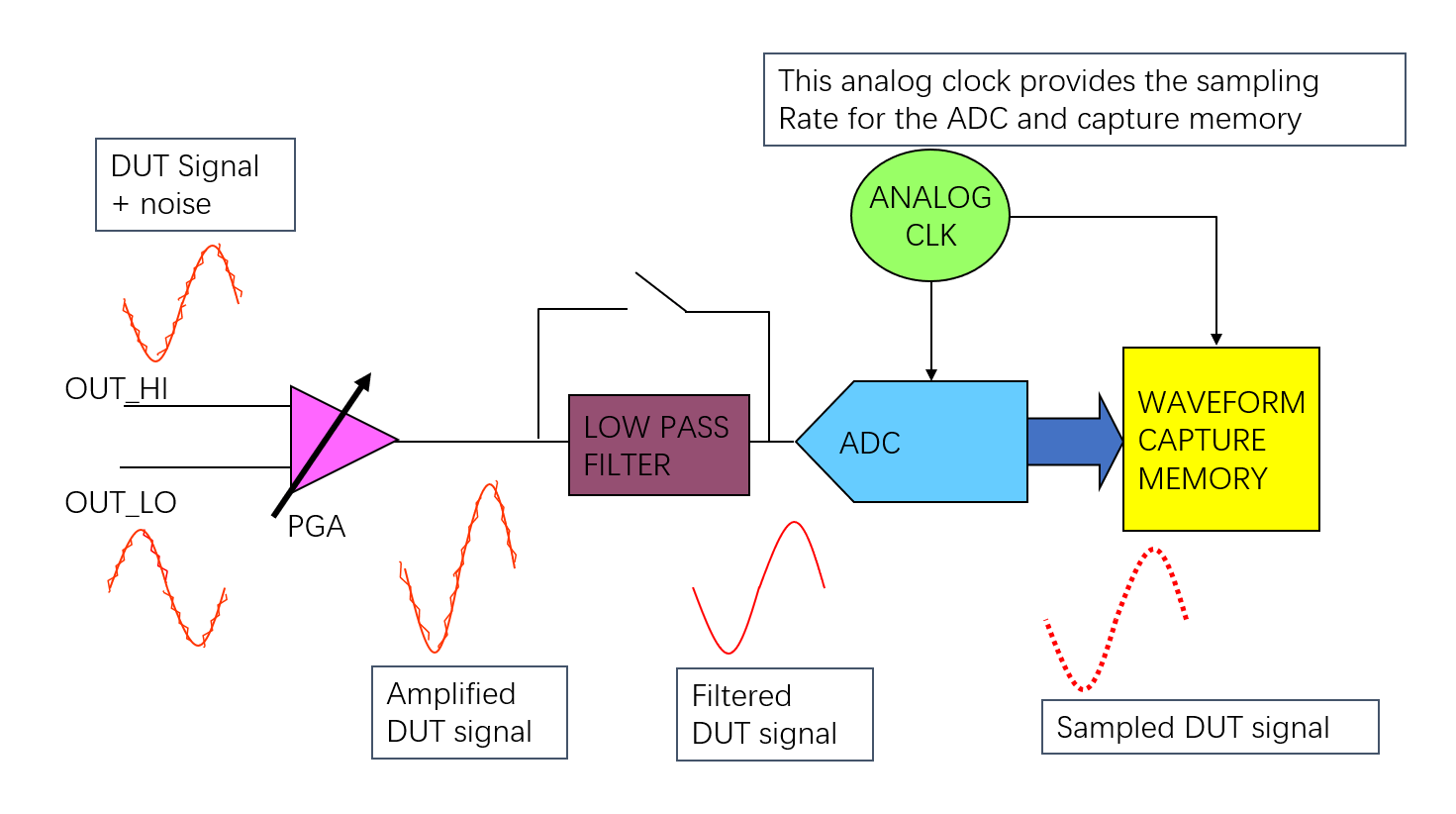
El filtro paso bajo limita el ancho de banda de la señal para eliminar componentes de frecuencia no deseados, como el ruido y las espurias, y proporciona anti-aliasing al atenuar las espurias que podrían ser aliasadas en la banda de paso del filtro durante la conversión del ADC.
Parámetros importantes del WD:
- Rango de Voltaje de Entrada Pico a Pico Máximo
- Resolución de la Forma de Onda (Resolución del ADC)
- Ancho de Banda
- Profundidad de Memoria de Captura de Forma de Onda
- Impedancia de Entrada
- Ruido, THD, SNR, espurias
Reloj
Los relojes analógicos y digitales se derivan de un reloj de referencia de todo el sistema. Si no hay una señal de sincronización de reloj, la desviación de tiempo puede llevar a resultados incorrectos.
Procesador de Señal Digital (DSP)
Procesador de Señal Digital (DSP) es un microprocesador especializado que realiza operaciones matemáticas en conjuntos de números digitales. En el DSP, se ejecutan varios algoritmos como la Transformada de Fourier Discreta (DFT) y la Transformada Rápida de Fourier (FFT) para transformar la información del dominio del tiempo al dominio de la frecuencia.
La arquitectura de un DSP está optimizada para permitir una rápida multiplicación, suma, cálculos de logaritmos, elevación al cuadrado y cálculos de raíz cuadrada.
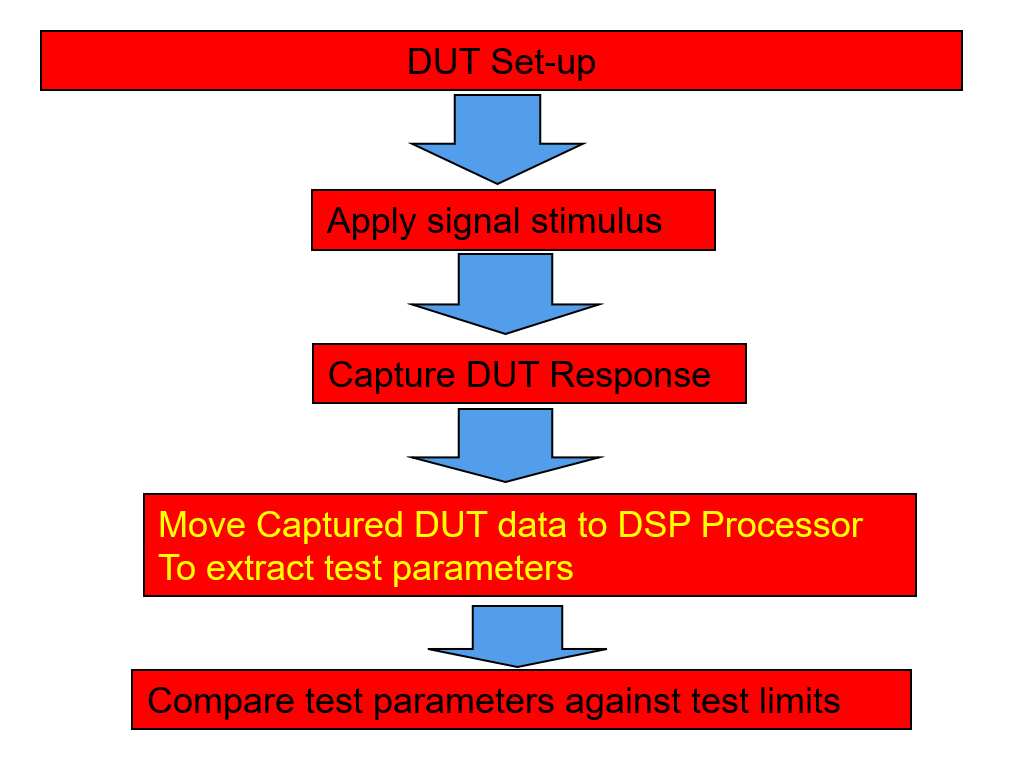
El probador llevará la señal capturada almacenada al procesador DSP a través de buses de datos.
Referencias y Agradecimientos
- Fundamentos de Pruebas Utilizando ATE
- Los Fundamentos de Pruebas de Señal Mixta de Brian Lowe
Original: https://wiki-power.com/ Esta publicación está protegida por el acuerdo CC BY-NC-SA 4.0 y debe ser reproducida con atribución.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.