Fundamentos de ADC y DAC

En el mundo real, la mayoría de las señales que encontramos son analógicas, como la temperatura, el sonido, la presión del aire, etc. Sin embargo, en el procesamiento y la transmisión de señales, se utiliza ampliamente la señal digital para reducir la interferencia de ruido. Por lo tanto, a menudo convertimos señales analógicas del mundo real en señales digitales mediante un ADC para su procesamiento, transmisión y almacenamiento, y luego las convertimos de nuevo en señales analógicas mediante un DAC para su presentación.

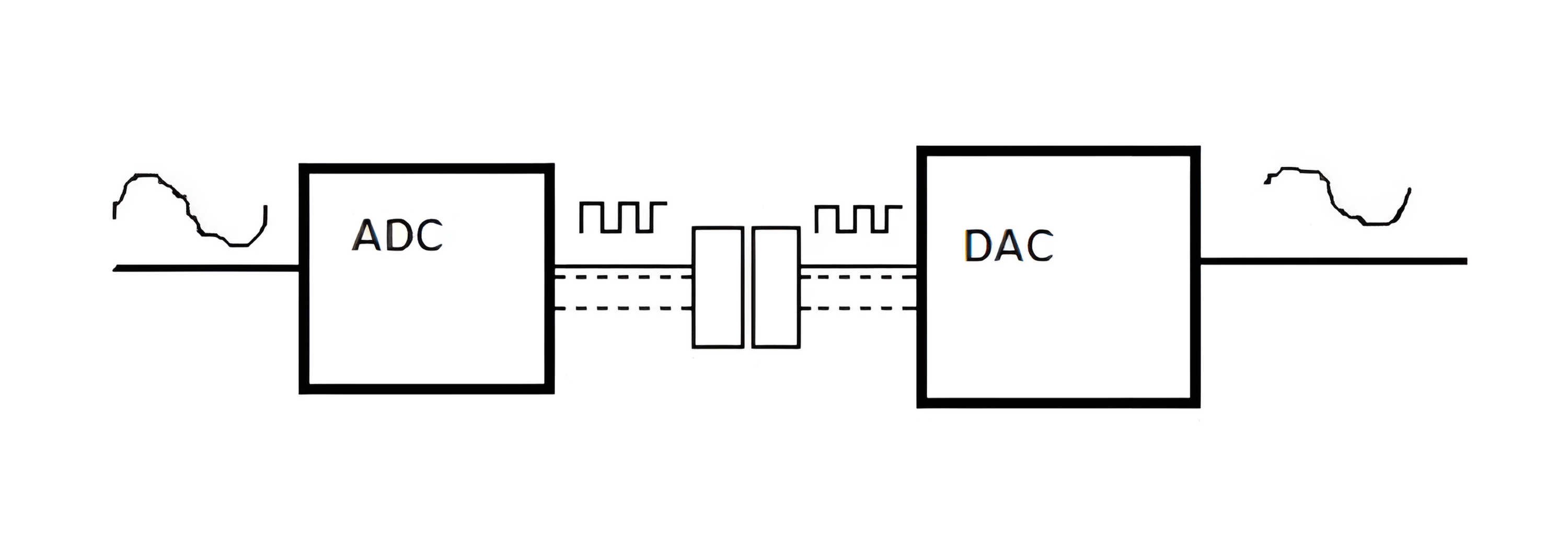
Es importante tener en cuenta que las señales analógicas del mundo real son continuas, lo que significa que tienen una resolución infinita. Sin embargo, después de convertirlas en señales digitales, perderemos cierta precisión, y tanto en tiempo como en amplitud, se convertirán en valores discretos.

Principios básicos de ADC

ADC (Conversor Analógico-Digital) se refiere a un convertidor que transforma señales analógicas del mundo real, como temperatura, presión, sonido o imágenes, en una forma digital más adecuada para su almacenamiento, procesamiento y transmisión.

Muestreo

Dado que la señal analógica de entrada es continua, mientras que la señal digital de salida es discreta, solo podemos realizar muestreos instantáneos y luego convertir los valores muestreados en cantidades digitales de salida antes de iniciar la próxima ronda de muestreo.

Para representar con precisión una señal de entrada analógica \(v_1\) como una señal \(v_s\), debemos cumplir al menos con el teorema de muestreo, que establece que la frecuencia de muestreo \(f_s\) debe ser al menos el doble de la frecuencia máxima de la señal de entrada analógica \(f_{i(max)}\) (generalmente se toma de 3 a 5 veces el valor, pero frecuencias muy altas requerirán velocidades de trabajo más rápidas, lo que aumenta los costos):

Si se cumple el teorema de muestreo, podemos utilizar un filtro pasa-bajos para restaurar \(v_s\) a \(v_1\). La ganancia de transferencia del filtro debe mantenerse constante por debajo de \(f_{i(max)}\) y disminuir rápidamente a cero antes de \(f_s-f_{i(max)}\).

Retención

Un circuito de retención permite que la señal se mantenga durante un cierto tiempo después del muestreo, lo que le da al ADC suficiente tiempo para realizar la conversión. Cuanto mayor sea la frecuencia de los impulsos de muestreo y cuanto más denso sea el muestreo, más valores se obtendrán del circuito de retención, y la señal de salida se asemejará más a la forma de onda de la señal de entrada. Los pasos básicos del circuito de muestreo y retención son los siguientes:

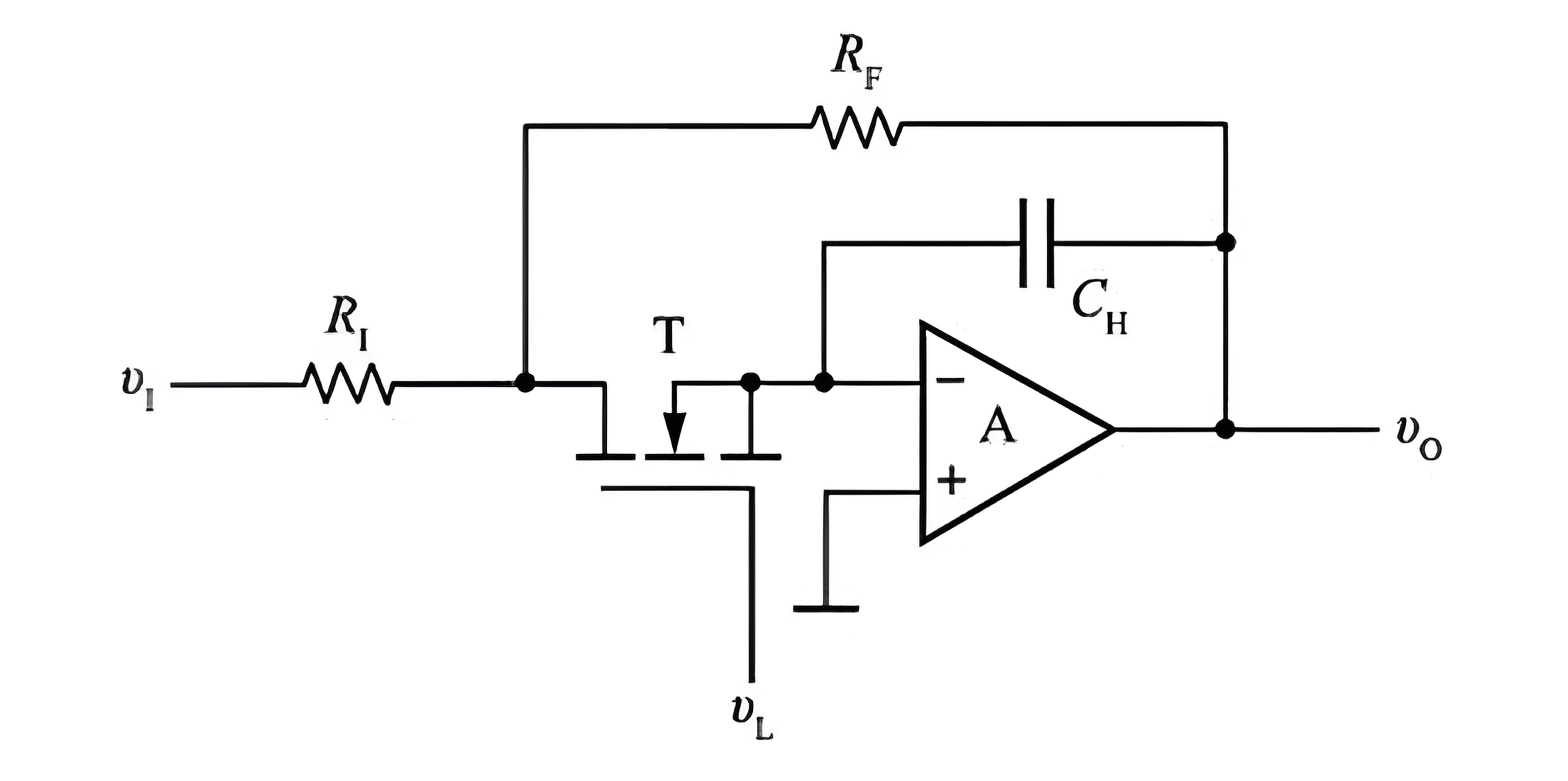
1. Cuando la señal de control de muestreo \(v_L\) está en alto, el transistor MOS \(T\) se enciende, y la señal \(v_1\) pasa a través de la resistencia \(R_1\) y el transistor MOS \(T\), cargando el condensador \(C_H\).
2. Si elegimos \(R_1=R_F\), al final de la carga, \(v_0=v_c=-v_1\).
3. Cuando la señal de control de muestreo \(v_L\) vuelve a caer, el transistor MOS \(T\) se apaga, y la tensión en el condensador \(C_H\) no experimenta un cambio brusco, lo que permite que \(v_0\) se mantenga durante un cierto tiempo y se registre el resultado del muestreo.

Cuantificación

Las cantidades digitales obtenidas a partir del muestreo deben ser múltiplos de una unidad mínima predefinida, en un proceso conocido como cuantificación. La unidad mínima de cuantización se denomina unidad de cuantización \(\Delta\). El valor de la cantidad representada por el bit menos significativo (LSB) en la señal digital es igual a \(\Delta\).

Dado que la tensión analógica es continua, no siempre es divisible por \(\Delta\), lo que da lugar a errores de cuantización.

Cuanto más fina sea la cuantización, menor será el error de cuantización, pero se necesitarán más bits en el código binario, lo que hace que el circuito sea más complejo.

Codificación

La representación de los resultados cuantificados en binario (u otras bases) se denomina codificación.

Tipos comunes de ADC

Tipo de comparador paralelo (Flash)

El ADC de tipo comparador paralelo, también conocido como Flash ADC, es un tipo de ADC directo que convierte directamente la tensión analógica de entrada en una cantidad digital de salida sin necesidad de conversiones intermedias. Está compuesto por una serie de comparadores de voltaje, donde cada comparador compara la señal de entrada con una tensión de referencia dividida de manera única. Las salidas de los comparadores se conectan a un circuito codificador que genera una salida binaria.

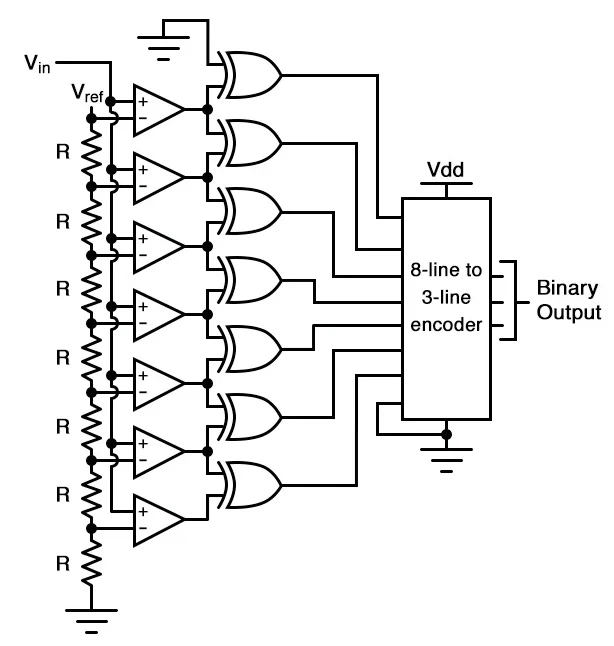
Es el más simple en teoría de funcionamiento y el más eficiente en velocidad de todos los tipos de tecnología ADC, limitado solo por las demoras de propagación de los comparadores y las compuertas. Desafortunadamente, para un número dado de bits de salida, requiere el mayor número de componentes.

El tipo de ADC en paralelo es el más rápido, pero tiene la desventaja de requerir múltiples comparadores de voltaje y circuitos de conversión de código a gran escala (los ADC en paralelo comunes tienen una resolución de 8 bits o menos).

Tipo de Aproximación Sucesiva

El ADC de Aproximación Sucesiva utiliza una estructura de circuito de retroalimentación de comparación. Está compuesto por comparadores, DAC, registros, fuente de pulsos de reloj y lógica de control, entre otros:

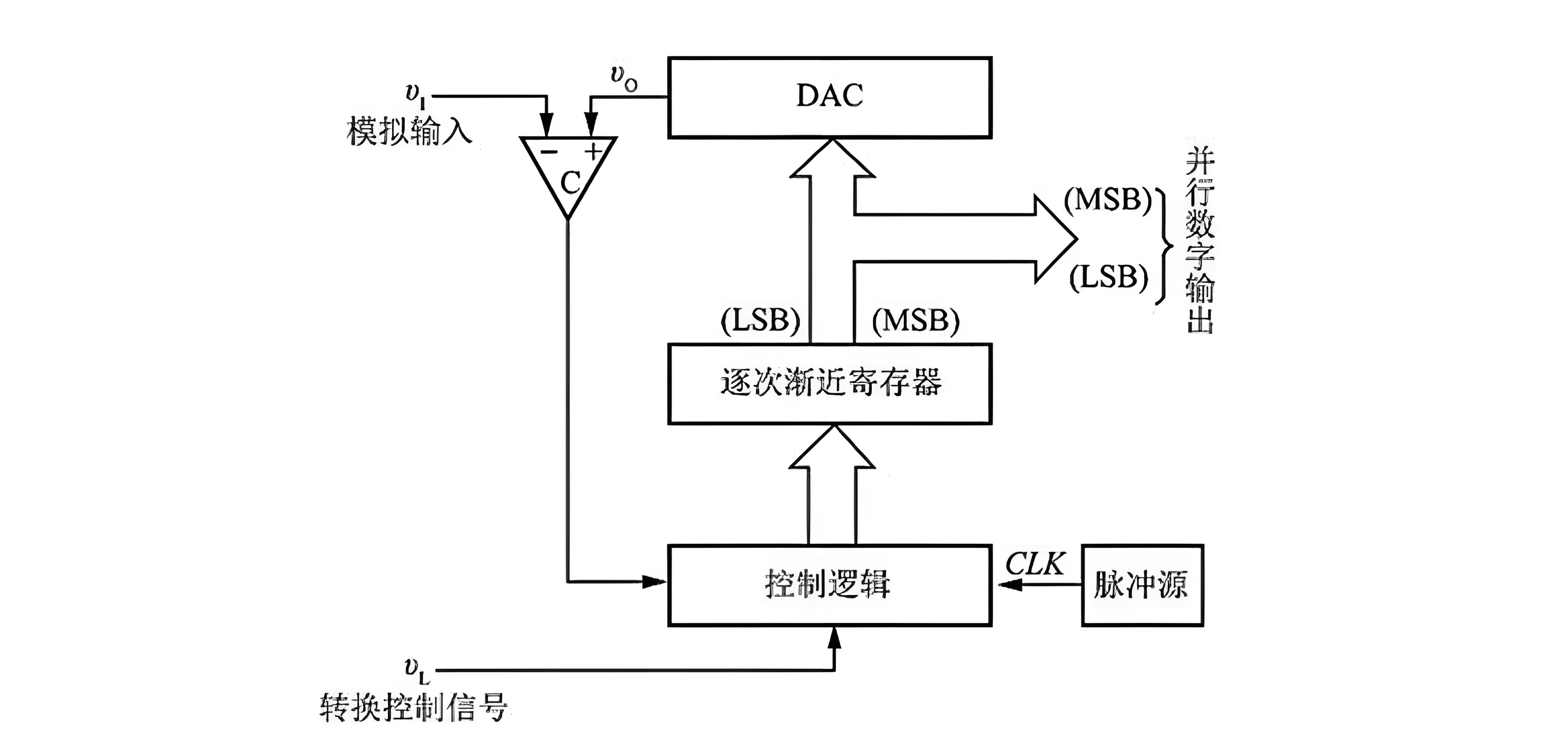
Su principio consiste en establecer un valor digital, obtener una tensión analógica de salida correspondiente a través del DAC y comparar secuencialmente esta tensión analógica con la señal de voltaje analógico de entrada, comenzando desde el bit más significativo. Si no son iguales, se ajusta el valor digital hasta que ambas tensiones analógicas sean iguales, y el valor digital final obtenido es el resultado de la conversión. Este proceso es similar a pesar un objeto en una balanza, primero agregando pesos grandes y luego agregando o reemplazando pesos más pequeños.

Las ventajas del ADC de Aproximación Sucesiva son su alta velocidad, bajo consumo de energía y una buena relación calidad-precio a baja resolución (12 bits o menos). La desventaja es que la velocidad de conversión suele ser promedio y el tamaño del circuito es mediano.

Tipo de Doble Integrador (V-T)

El ADC de Doble Integrador es un tipo de ADC indirecto que convierte la señal de voltaje analógico de entrada en una señal de ancho de pulso de tiempo proporcional. Luego, dentro de ese ancho de pulso de tiempo, cuenta los pulsos de un reloj de frecuencia fija, y el valor de conteo resultante es una representación digital de la señal de entrada analógica. Por lo tanto, a este tipo de ADC también se le llama ADC de Transformación de Voltaje-Tiempo (V-T).

El ADC de Doble Integrador consta de integradores, comparadores, contadores, lógica de control y una fuente de señal de reloj, entre otros, como se muestra en la siguiente imagen:

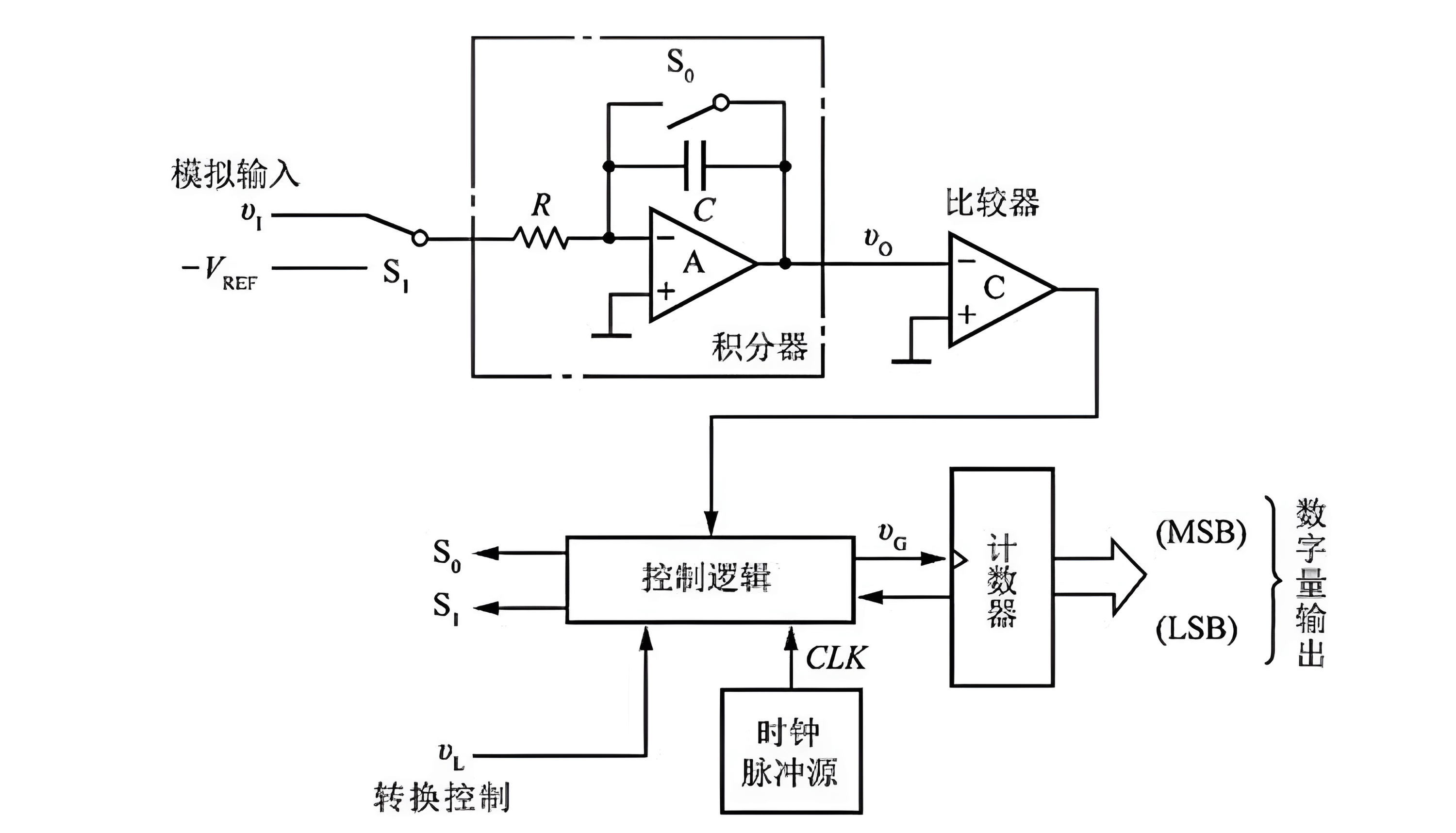
Las ventajas del ADC de Doble Integrador son su estabilidad en el rendimiento (debido a las dos etapas de integración, las diferencias en los parámetros RC se eliminan) y su resistencia a las interferencias (el proceso de integración no se ve afectado significativamente por el ruido). La desventaja es que la velocidad de conversión es baja, ya que la precisión de conversión depende del tiempo de integración.

Tipo Σ-Δ

El ADC de Modulación Σ-Δ difiere de los ADC en paralelo y de Aproximación Sucesiva mencionados anteriormente. En lugar de cuantificar y codificar el valor absoluto de la señal de muestreo, cuantifica y codifica la diferencia (incremento) entre los valores de muestreo adyacentes. Su estructura básica se muestra a continuación:

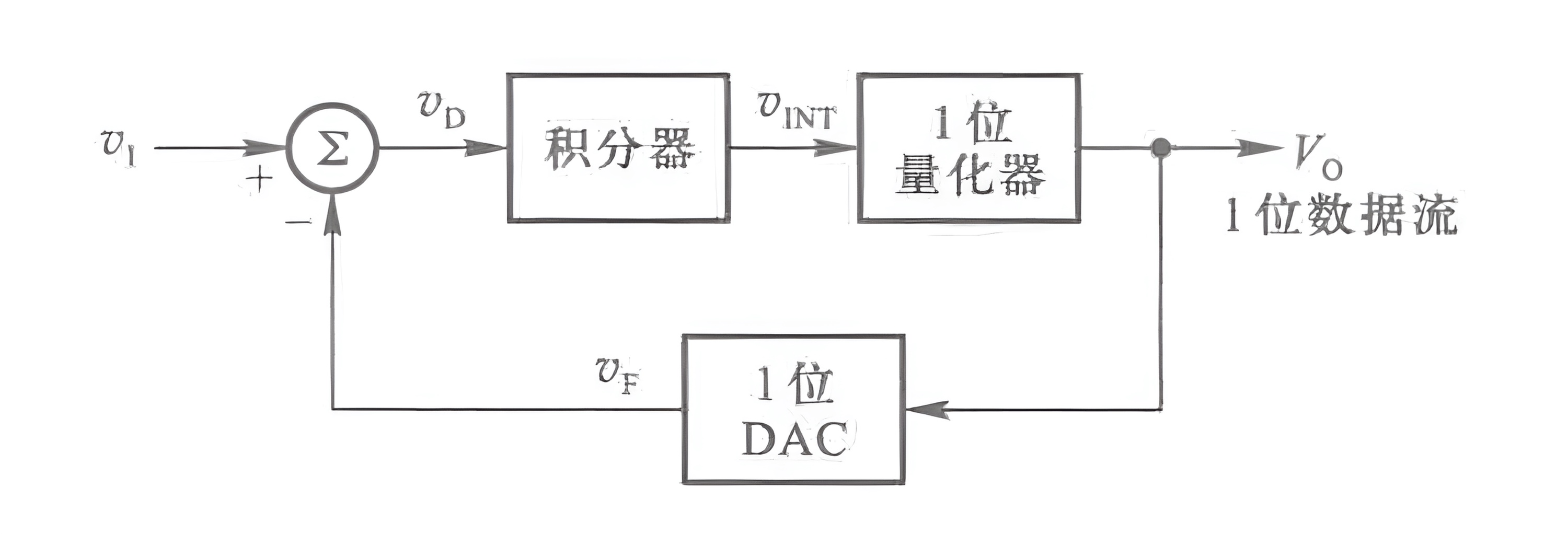
Está compuesto por un integrador de voltaje lineal, un cuantizador de salida de 1 bit, un DAC de entrada de 1 bit y un circuito de suma. El valor de la señal digital \(V_0\) se obtiene después del procesamiento del cuantizador y se convierte en la señal analógica \(V_F\) a través del DAC, que se retroalimenta al circuito de suma en la entrada, donde se resta de la señal de entrada \(v_1\) para obtener la diferencia \(v_D\). El integrador realiza una integración lineal de \(v_D\), produciendo una tensión de salida \(v_{INT}\) que se cuantifica en una señal digital de 1 bit a través del cuantizador. Debido al uso de un cuantizador de 1 bit, en un estado de funcionamiento continuo, la señal de salida \(V_0\) está formada por una secuencia de datos que consiste en 0 y 1.

Las ventajas del ADC de Modulación Σ-Δ son su capacidad para lograr mediciones de alta resolución con facilidad. La desventaja es que tiene una velocidad de conversión baja y un tamaño de circuito grande.

Tipo de Transformación de Voltaje a Frecuencia (V-F)

El ADC de Transformación de Voltaje a Frecuencia (V-F) es otro tipo de ADC indirecto. Está compuesto principalmente por un convertidor V-F (Oscilador Controlado por Voltaje, VCO), un contador con puertas de control de reloj, registros, un disparador monostable y más, como se muestra a continuación:

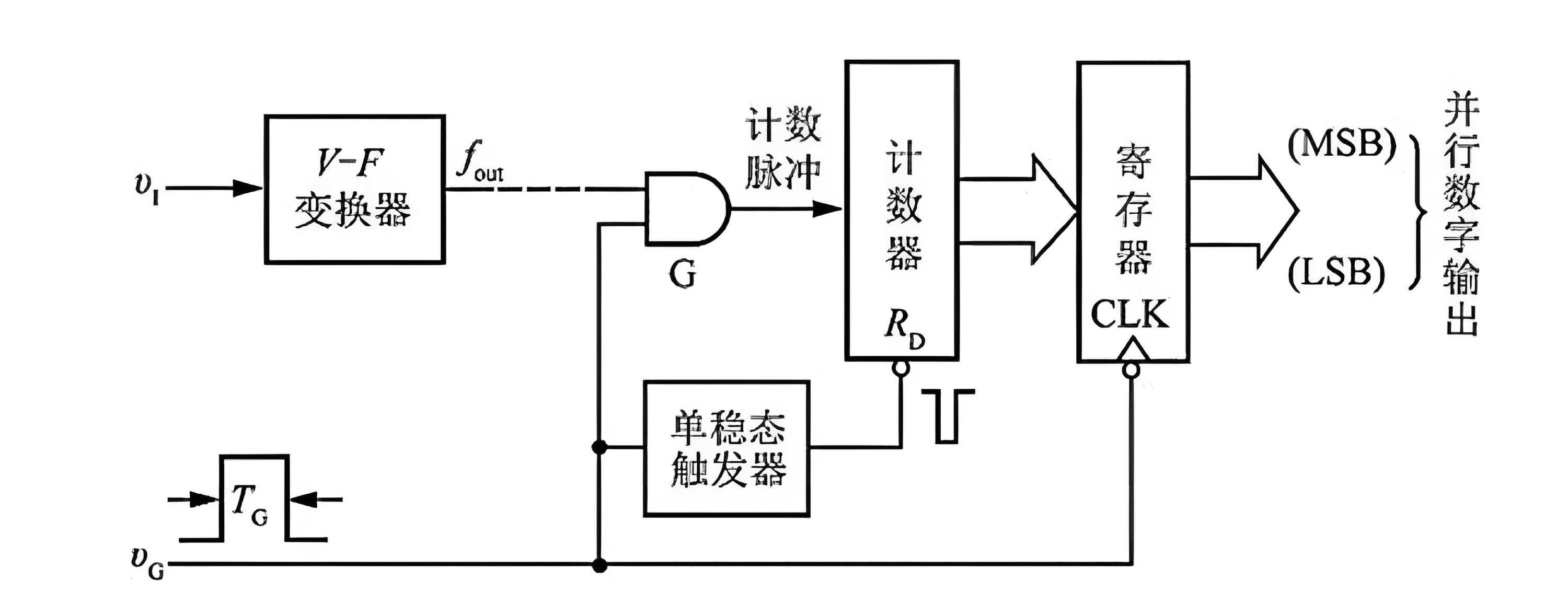
Su principio es el siguiente:

• Convierte la señal de voltaje analógico de entrada en una señal de frecuencia correspondiente.
• Realiza un conteo de la tasa de señal de frecuencia dentro de un tiempo fijo.
• El resultado del conteo es proporcional a la amplitud de la señal de entrada.

Parámetros Principales de los ADC

• Resolución: La cantidad de cambio en la señal analógica requerida para un cambio de un valor numérico de salida, generalmente se expresa en términos de la cantidad de bits binarios. Una resolución de "n" significa que es 1 entre 2 elevado a la "n" de la escala completa "Fs".

• Error de cuantificación: El error causado por la cuantificación de la señal analógica debido a la cantidad finita de bits en un convertidor analógico a digital (ADC). Para representar con precisión una señal analógica, se necesitarían un número infinito de bits en el ADC, por lo que todos los dispositivos ADC tienen un error de cuantificación. La mayor discrepancia entre la curva característica de conversión de un ADC con resolución limitada y la curva característica de un ADC con resolución infinita se conoce como error de cuantificación.

• Tasa de conversión: La cantidad de conversiones realizadas por segundo.

• Rango de conversión: El voltaje máximo que un ADC puede medir, generalmente igual al voltaje de referencia. Superar este voltaje puede dañar el ADC. Cuando la señal es pequeña, se puede considerar la reducción del voltaje de referencia para mejorar la resolución. Cambiar el voltaje de referencia también afectará los valores de conversión correspondientes, por lo que es importante que el voltaje de referencia sea estable y no tenga armónicos de alto orden.

• Error de offset: Cuando la señal de entrada a un ADC es cero, pero la salida del ADC no es cero.

• Error de escala completa: La diferencia entre la señal de entrada correspondiente a la salida de escala completa de un ADC y el valor de entrada ideal.

• Linealidad: La máxima desviación entre la función de transferencia real de un ADC y la línea ideal.

Principios Básicos de DAC

DAC (Convertidor Digital-Analógico) se refiere a un convertidor que transforma una cantidad digital en una señal analógica proporcional, ya sea en forma de voltaje o corriente. Por ejemplo, una computadora puede generar una salida digital que varía desde 00000000 hasta 11111111, y un DAC la convierte en un voltaje que va desde 0 hasta 10V. En términos básicos, los DAC se dividen en dos categorías: sumadores de corriente y divisores.

Tipos Comunes de DAC

Árbol de Interruptores

El DAC tipo árbol de interruptores es el más simple y directo, compuesto por una red de resistencias divisoras y un conjunto de interruptores en cascada:

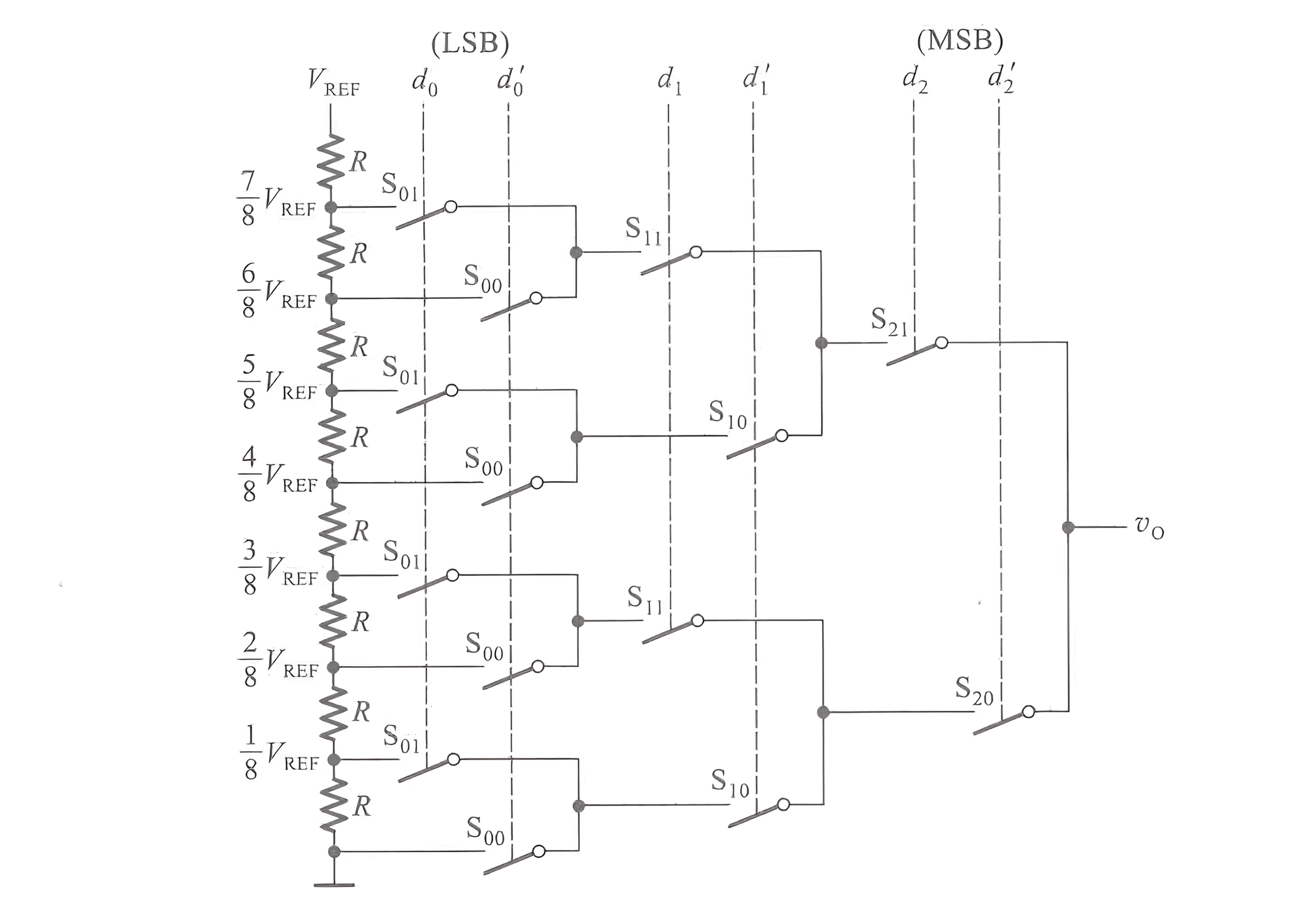
Estos interruptores son controlados por 3 bits de entrada, \(d_0, d_1, d_2\), y se calcula de la siguiente manera:

Para un DAC tipo árbol de interruptores con entrada binaria de n bits, la salida es:

La ventaja del DAC tipo árbol de interruptores es que utiliza un solo tipo de resistencia, y no requiere una corriente significativa en la salida. Sin embargo, la desventaja es que utiliza una gran cantidad de interruptores.

Red de Resistencias Ponderadas

El término "ponderado" se refiere a los valores que representa cada bit en un número binario. Por ejemplo, en un número binario de n bits \(D_n=d_{n-1}d_{n-2}...d_1 d_0\), el peso de cada bit desde el bit más significativo (MSB) hasta el menos significativo (LSB) es \(2^{n-1},2^{n-2}...2^1,2^0\).

El principio de funcionamiento de un DAC de red de resistencias ponderadas (que produce una salida de voltaje) se muestra en el siguiente diagrama (para 4 bits), y consta de una red ponderada de resistencias, 4 interruptores analógicos y un amplificador sumador:

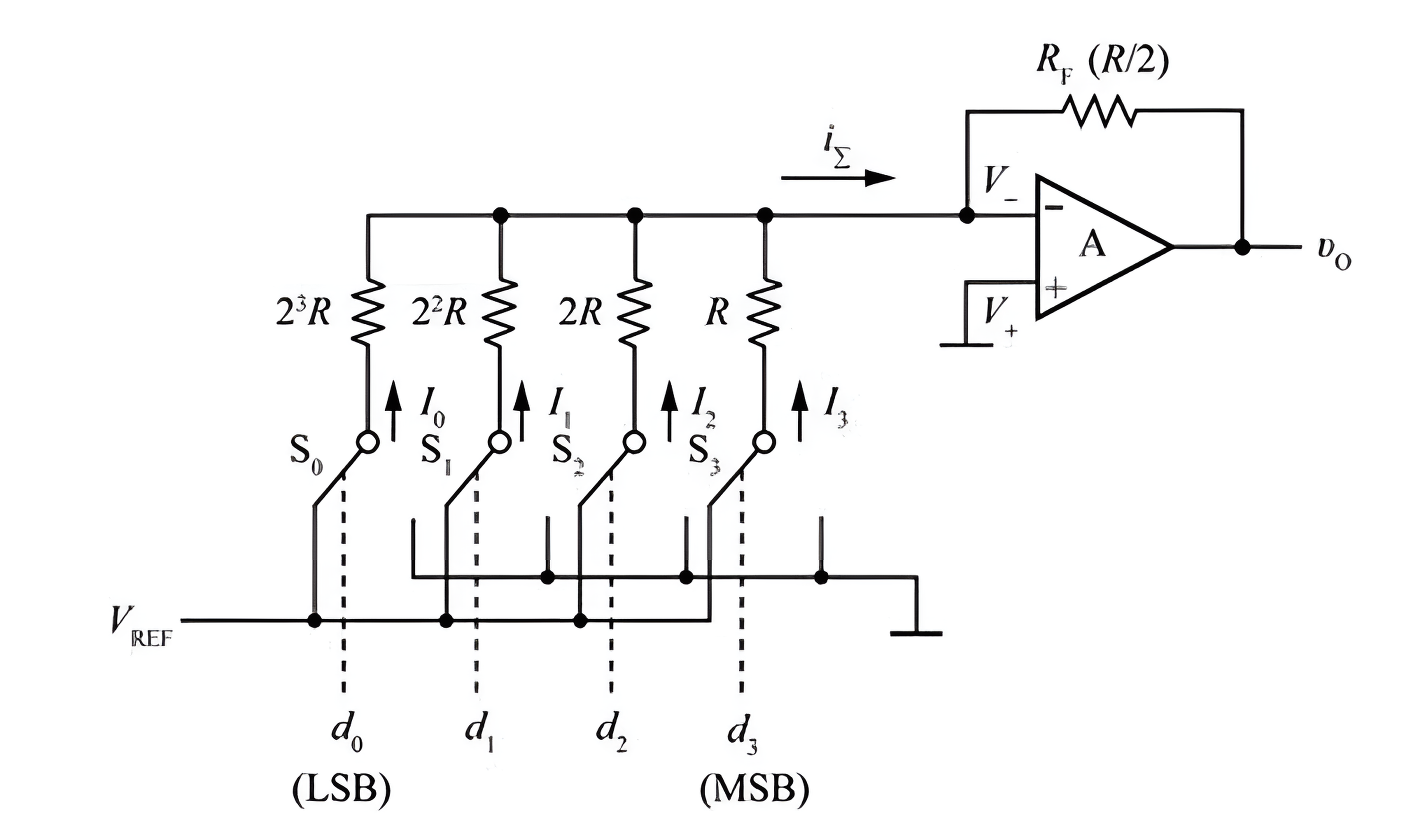
Donde \(S_0,S_1,S_2,S_3\) son 4 interruptores electrónicos, controlados por las señales \(d_0,d_1,d_2,d_3\). Cuando la entrada es 1, el interruptor se conecta a \(V_{REF}\), y cuando la entrada es 0, se conecta a tierra. Cuando \(d_i=1\), la corriente fluye hacia el amplificador sumador. Cuando \(d_i=0\), la corriente se bloquea. El amplificador sumador, con retroalimentación a través de \(R_F\), ajusta la tensión en \(V_-\) para mantenerla igual a \(V_+\) (0V).

Suppose the operational amplifier is an ideal device (with zero input current), then we can derive:

And since \(V_-\approx 0\), the currents in each branch can be calculated as follows:

Where \(d_n\) can be either 0 or 1. Substituting these values into the previous equation, and assuming the feedback resistor \(R_F\) is equal to \(\frac{R}{2}\), we can obtain the output voltage:

Furthermore, for an n-bit weighted resistor network DAC with a feedback resistor of \(R_F=\frac{R}{2}\), the output voltage can be calculated as:

Therefore, the analog output voltage is directly proportional to the digital input \(D_n\), and its range varies from 0 to \(-\frac{2^n-1}{2^n}V_{REF}\). On the other hand, if you need a positive output voltage, you should provide a negative \(V_{REF}\).

The advantage of the weighted resistor network DAC is its simplicity, but the disadvantage is that the resistor values can differ significantly, leading to potential accuracy issues in practice. To improve this, a double-pole weighted resistor network can be used, which is not discussed here but doesn't fundamentally solve the problem.

Inverted T-Resistor Network

To address the issue of significant resistor value differences in weighted resistor network DACs, an inverted T-resistor network DAC can be employed. It uses only two resistor values, R and 2R (hence, it's called R2R DAC), and it greatly contributes to control precision:

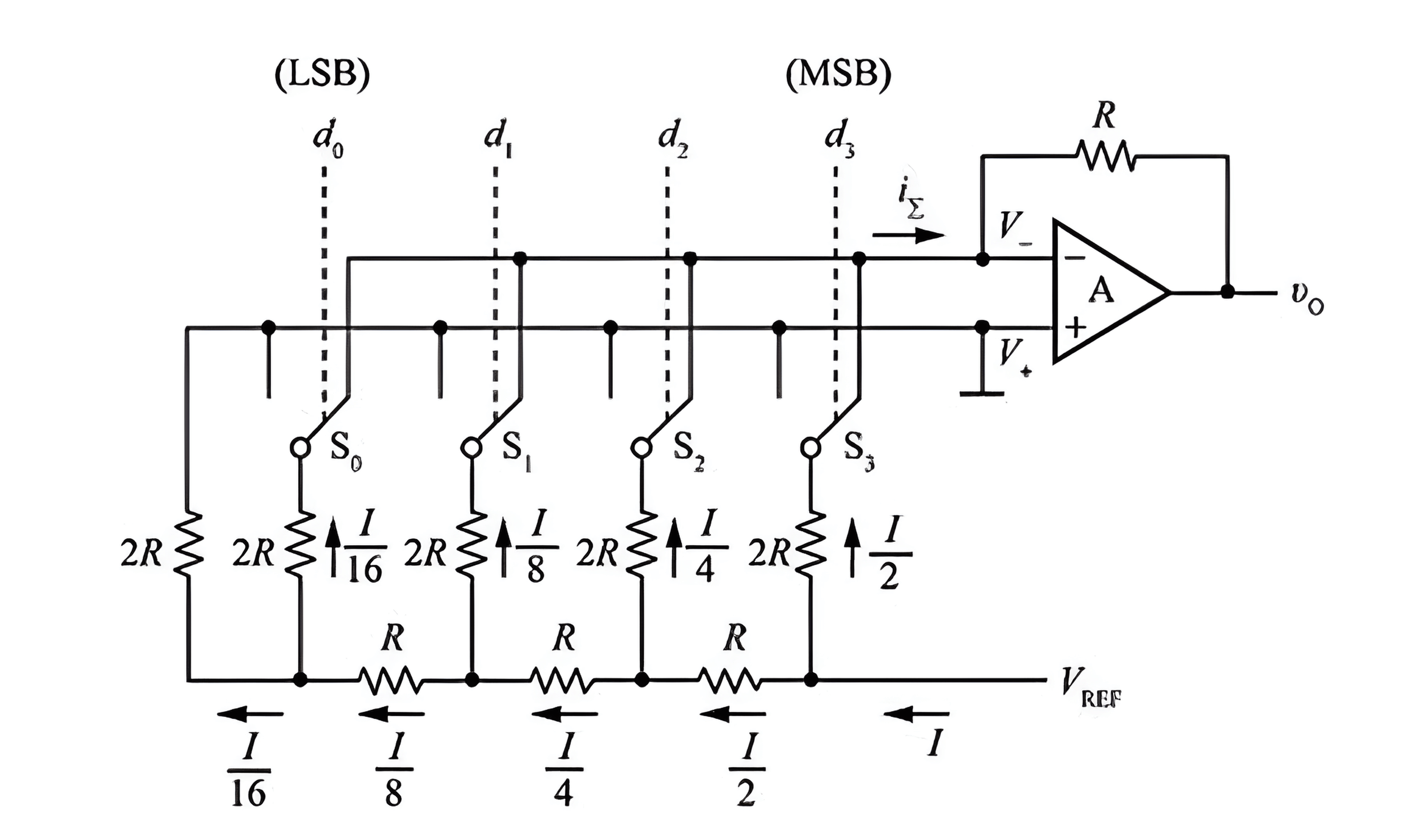
When the feedback resistor of the summing amplifier has a resistance value of R, the output voltage is:

As you can see, the calculation formula for the inverted T-resistor network is the same as that of the weighted resistor network DAC.

Weighted Current Type

When analyzing the weighted resistor network and inverted T-resistor network, we treat analog switches as ideal devices. However, in reality, they have some on-resistance and voltage drop, and their consistency may vary, leading to conversion errors that affect accuracy. The solution is to use a weighted current type DAC, which includes a set of constant current sources. Each current source's magnitude is half that of the previous one, and they are directly proportional to the binary input bits. The use of constant current sources eliminates the influence of switch on-resistance and voltage drop on the branch currents.

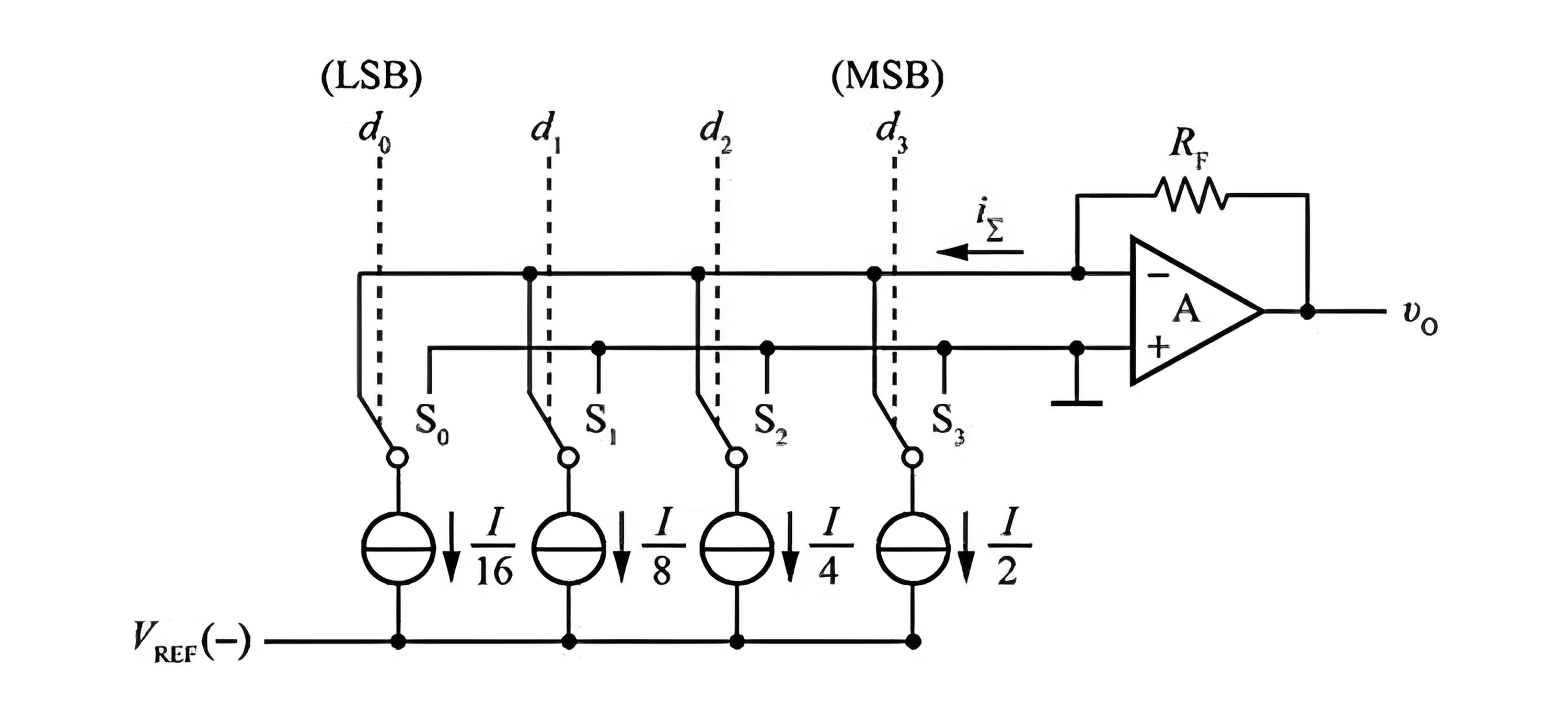
When a certain bit of the digital input is 1, the corresponding switch connects the constant current source to the input of the operational amplifier. When the input code is 0, the corresponding switch connects to ground. Therefore, the output voltage is given by:

Main DAC Parameters

• Resolution: The ratio of the smallest output voltage (corresponding to a digital input of 1) to the maximum output voltage (corresponding to all bits being 1 in the input). Generally expressed in terms of the number of input bits.

• Conversion Range: The maximum voltage that the DAC can output, typically in relation to the reference voltage or its multiples.

• Settling Time: The time it takes for the DAC to produce the analog output after a digital input is applied.

• Conversion Accuracy: Similar to ADC's conversion accuracy.

References and Acknowledgments

• 《Guía de Diseño de Aplicaciones ADC/DAC》
• Conversión Analógica a Digital y Conversión Digital a Analógico
• ADC y DAC (Convertidores Analógico a Digital y Digital a Analógico)
• Exploración de los Principios del DAC
• 《Referencia de Bolsillo para Ingenieros Analógicos》
• 《Tecnología Electrónica Digital (Sexta Edición) por 阎石》

Dirección original del artículo: https://wiki-power.com/
Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.

Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.