Fundamentos de Circuitos Digitales
Sistemas Numéricos y Códigos
Sistema Numérico: Reglas para representar cantidades. Incluye la composición de cada dígito y las reglas de acarreo de posición baja a posición alta, como el sistema decimal. Código: Reglas para representar cosas, como las reglas seguidas al codificar.
Circuito Analógico: Representa información mediante valores continuos de voltaje o corriente. Circuito Digital: Representa información mediante una secuencia discreta de voltajes.
Bases numéricas comunes: 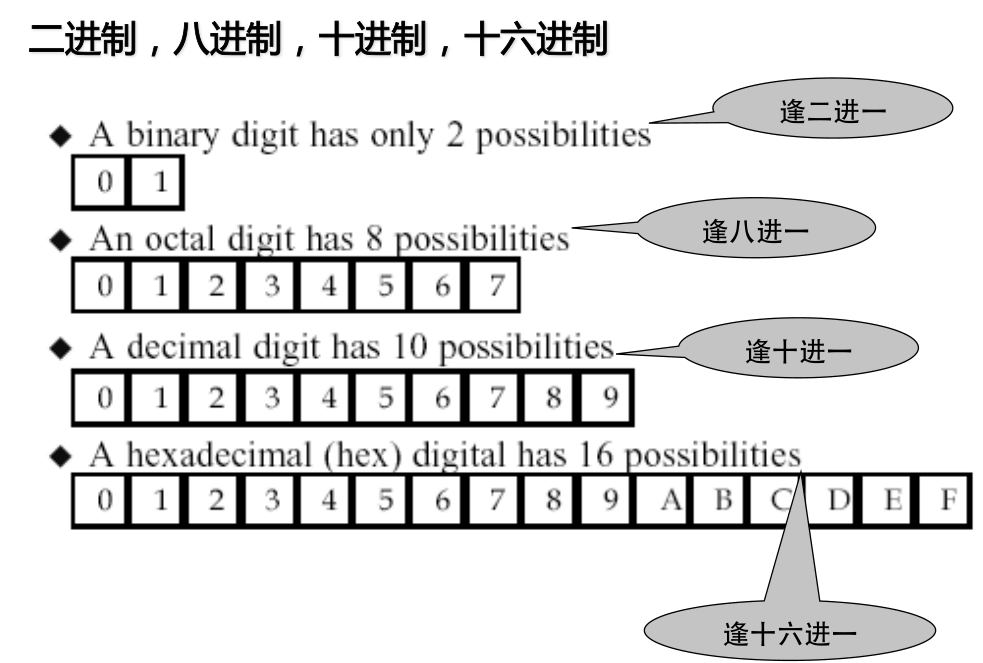
Conversión de cualquier base a decimal:
\((526)_8=5*8^2+2*8^1+6*8^0=(342)_{10}\)
\((2A.7F)_H=2*16^1+10*16^0+7*16^{-1}+15*16^{-2}=(42.4960937)_D\)
\(D=\sum K_iN^i\)
Complemento de Dos en Binario
- El bit más significativo es el bit de signo (0 para positivo, 1 para negativo).
- El complemento de dos de un número positivo es igual a su representación original.
- El complemento de dos de un número negativo es igual a invertir cada bit y sumar 1.
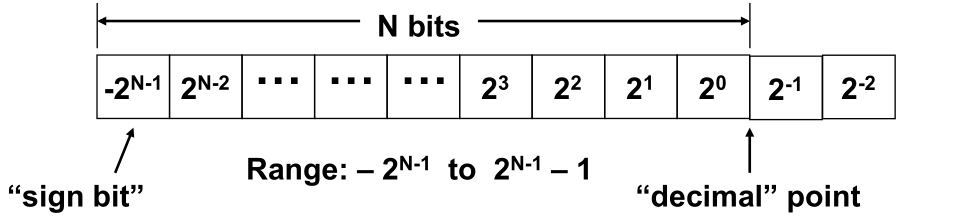
+5 = (0 0101)
-5 = (1 1011)1101.0110
= –2 3 + 2 2 + 2 0 + 2 -2 + 2 -3
= – 8 + 4 + 1 + 0.25 + 0.125
= – 2.625
Códigos
Códigos de longitud fija:
- Código BCD de 4 bits
- ASCII
- Código Gray: El orden de codificación cambia secuencialmente, y cuando cambia en el orden de la tabla, solo un bit adyacente cambia de estado.
Fundamentos del Álgebra de Boole
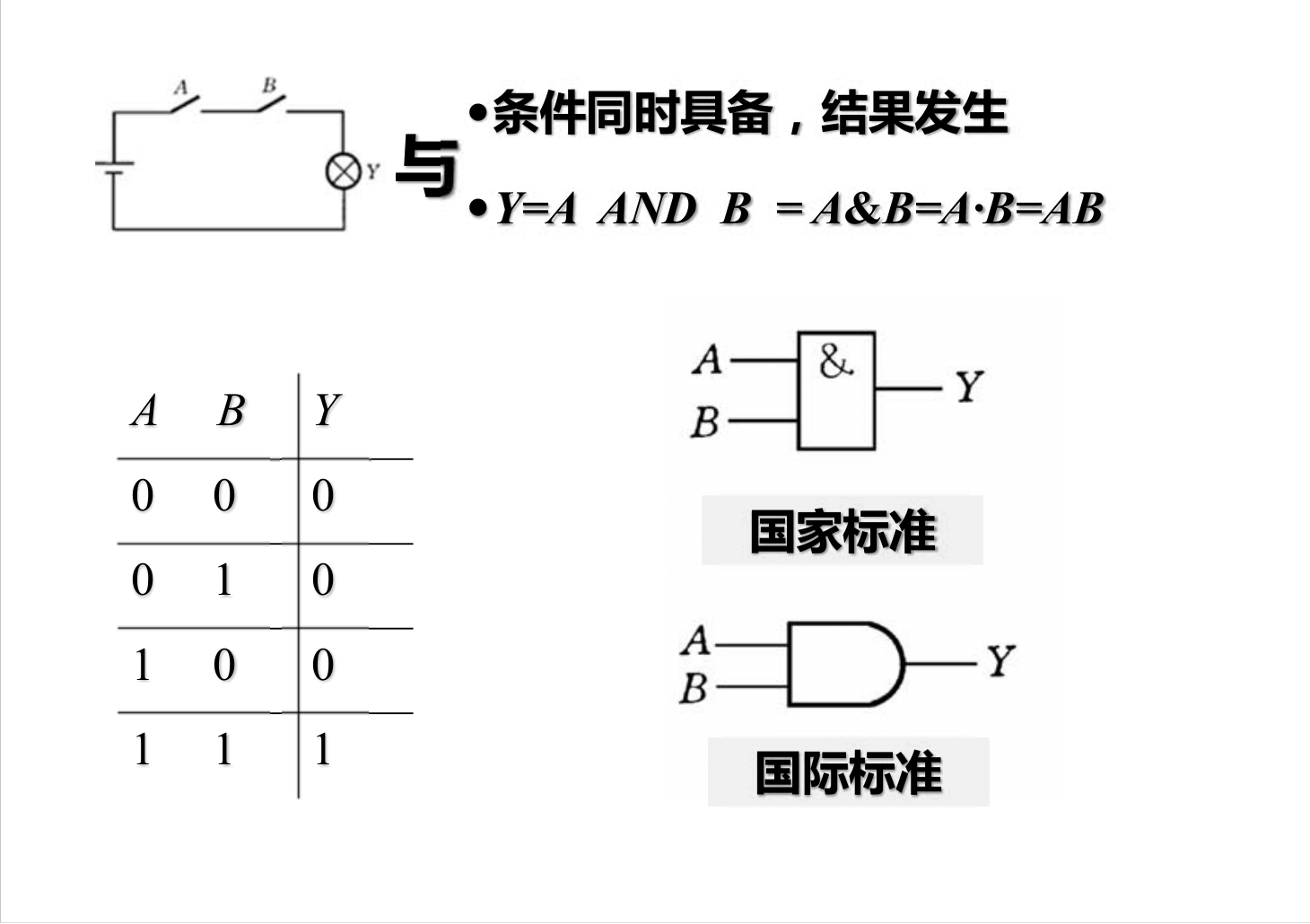
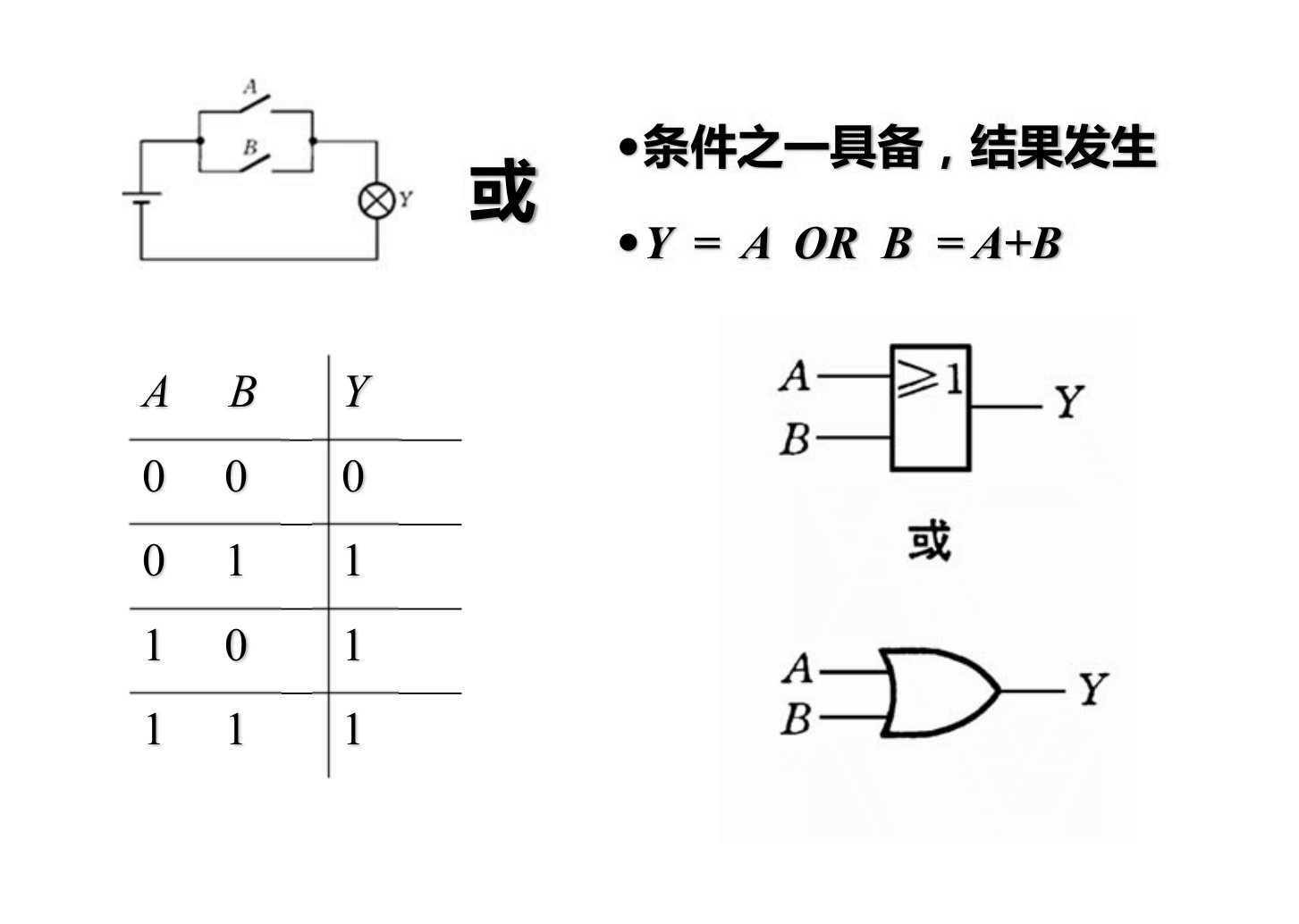
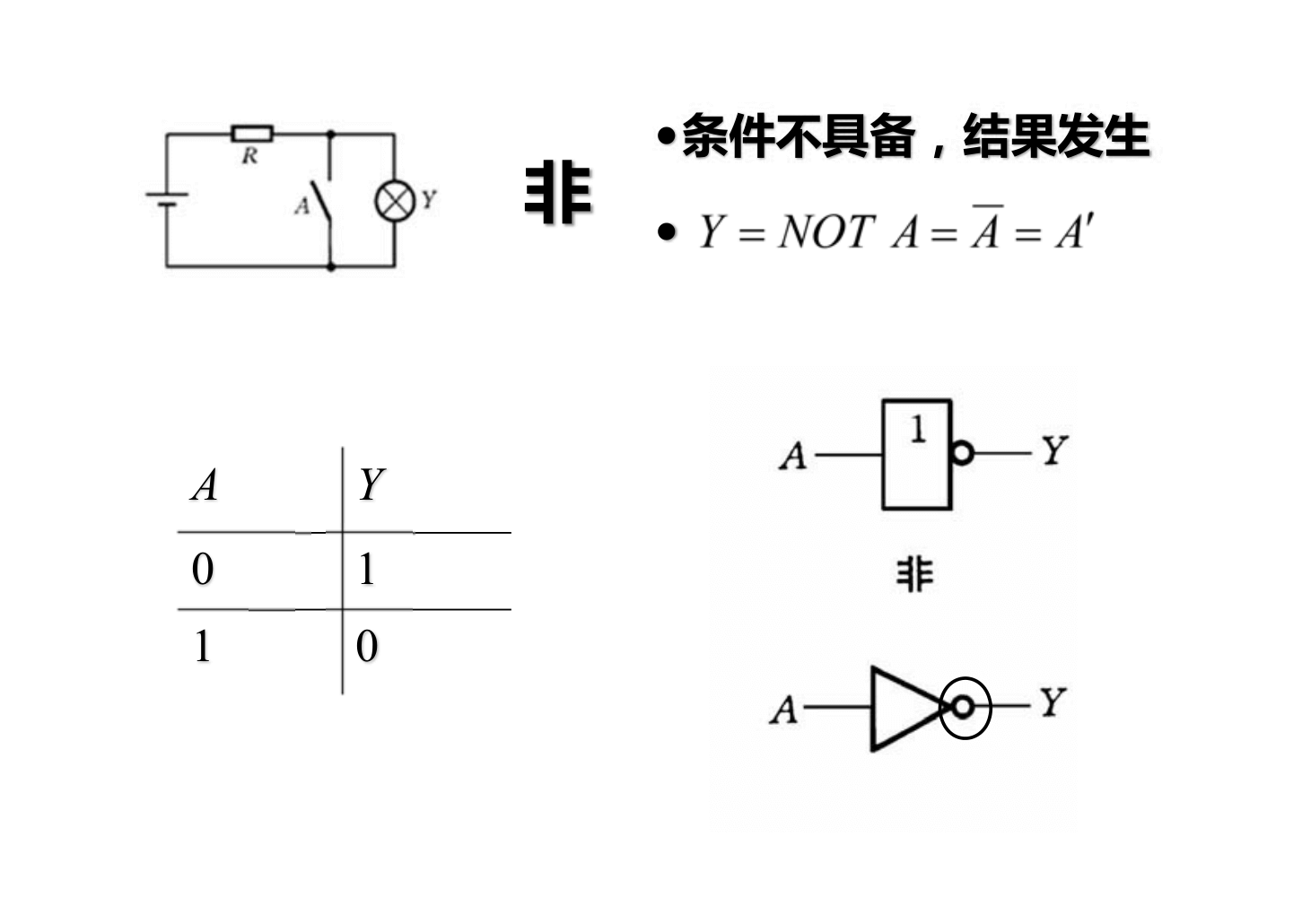
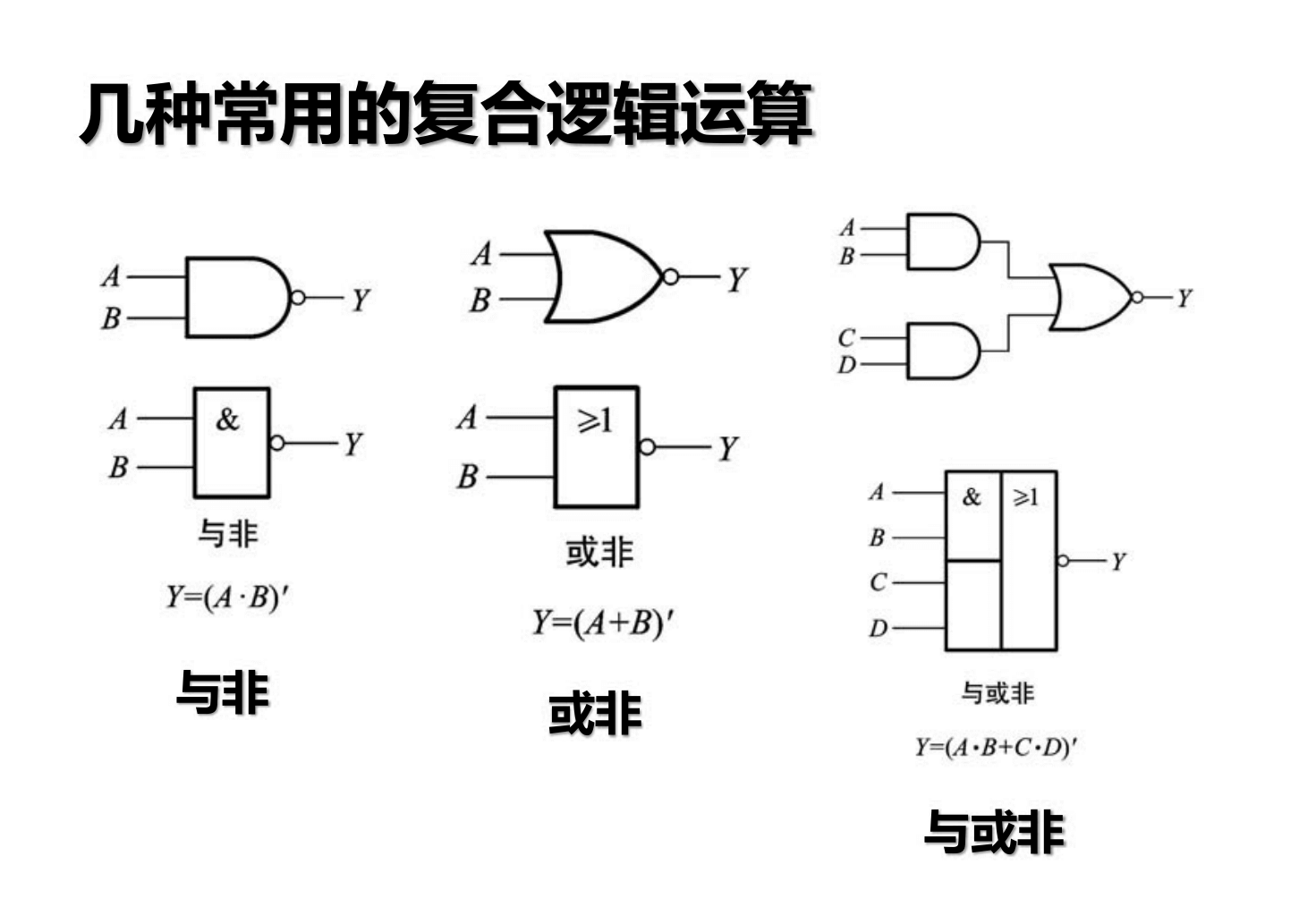
XOR: 1 si los bits son diferentes, 0 si son iguales
\(Y=A'B+AB'\) 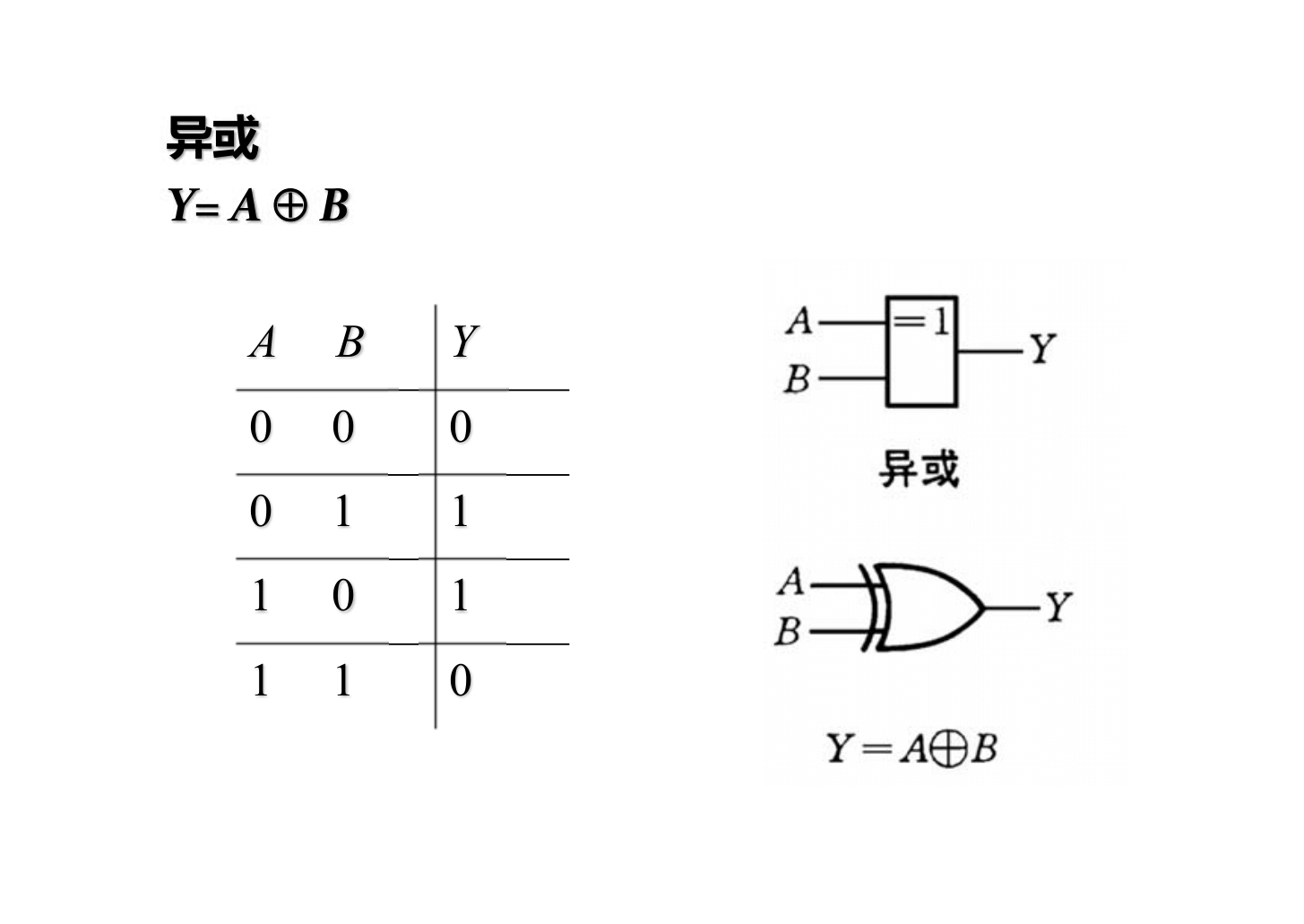
XNOR: 1 si los bits son iguales, 0 si son diferentes \(Y=AB+A'B'\) 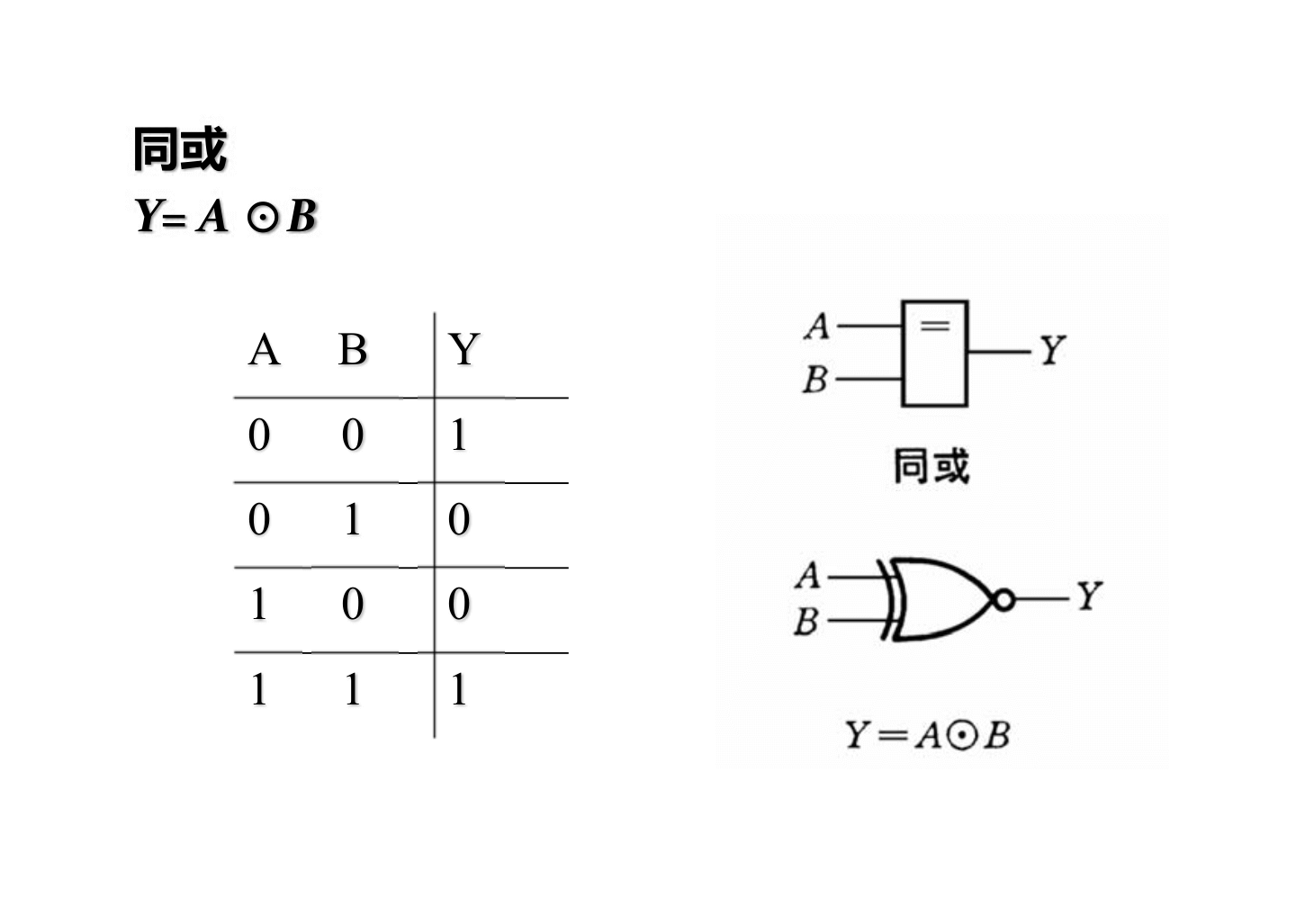
Fórmulas Básicas de Operaciones Lógicas
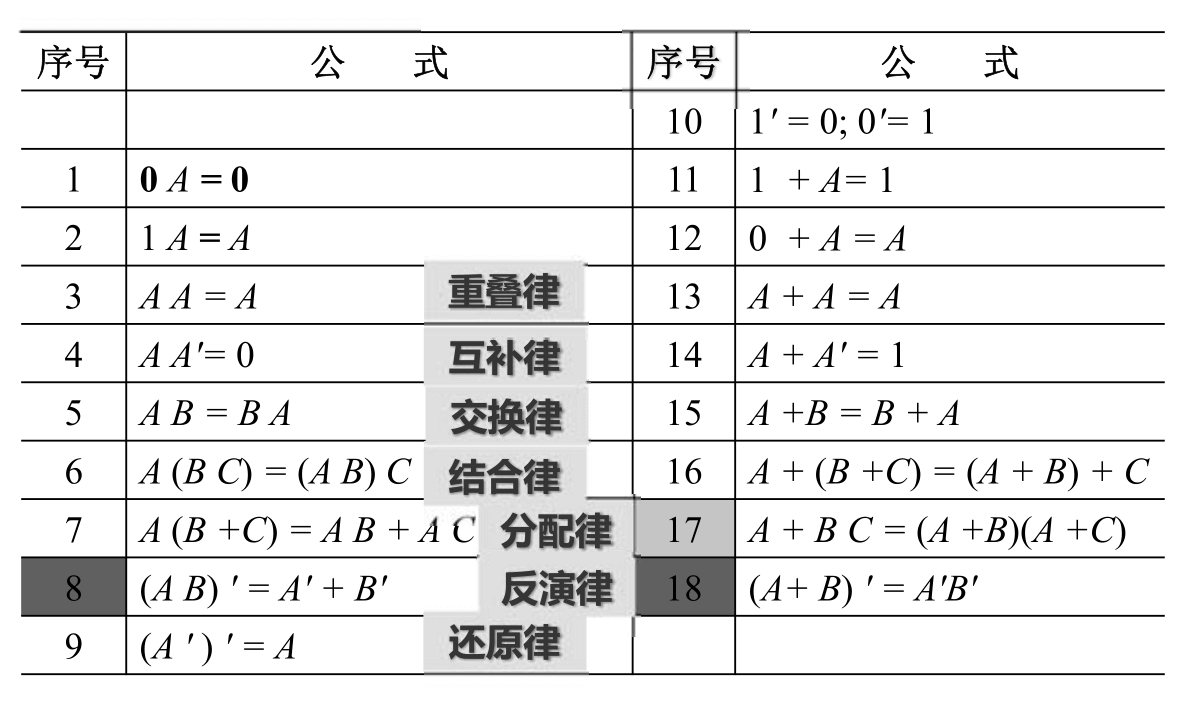
\((A B) ' = A' + B'\)
\((A+ B)' = A'B'\)
\(A + B C = (A +B)(A +C)\)
Fórmulas Comunes de Operaciones Lógicas

Teoremas Básicos del Álgebra de Boole


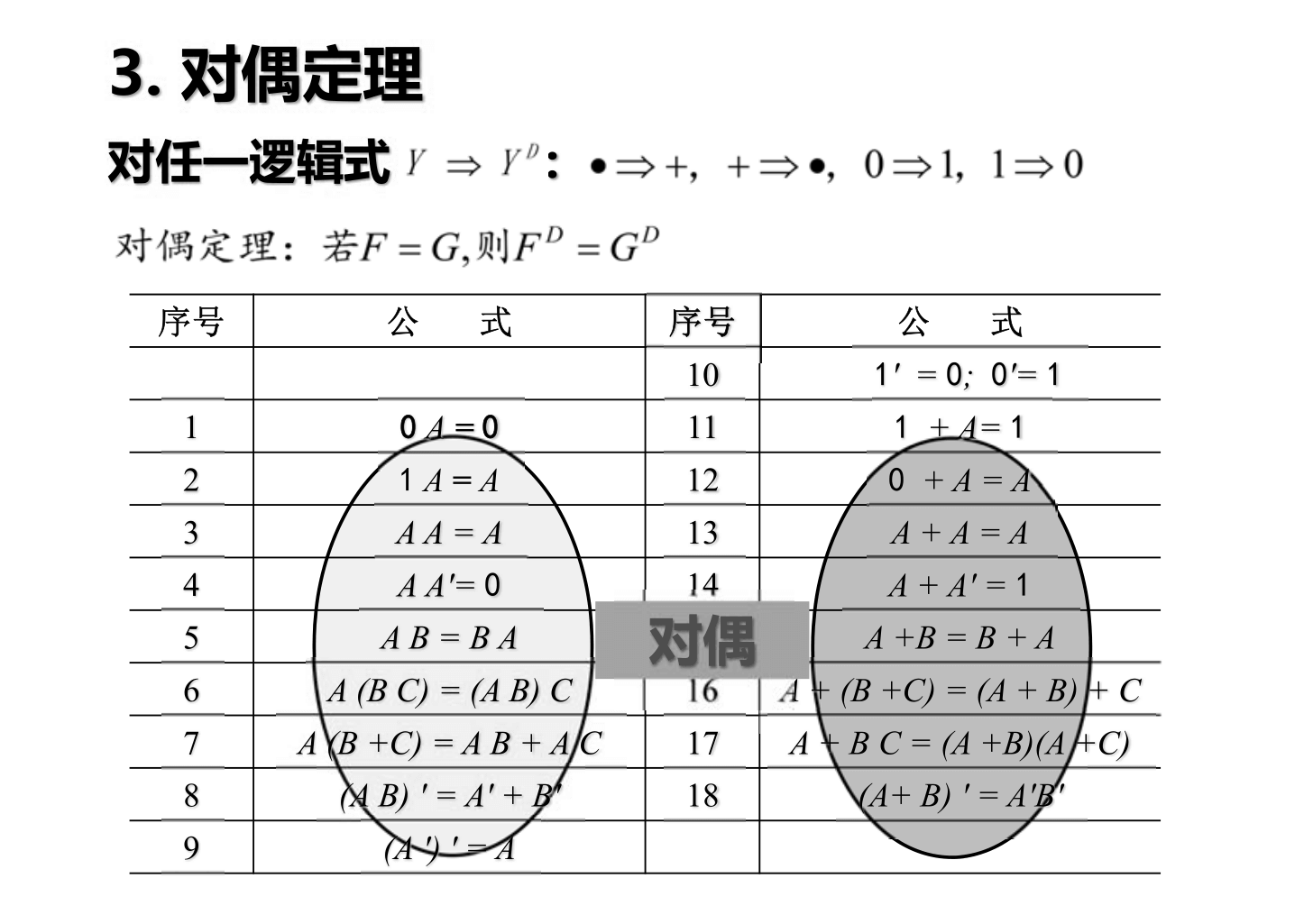
Métodos de Representación de Funciones Lógicas
- Tabla de verdad
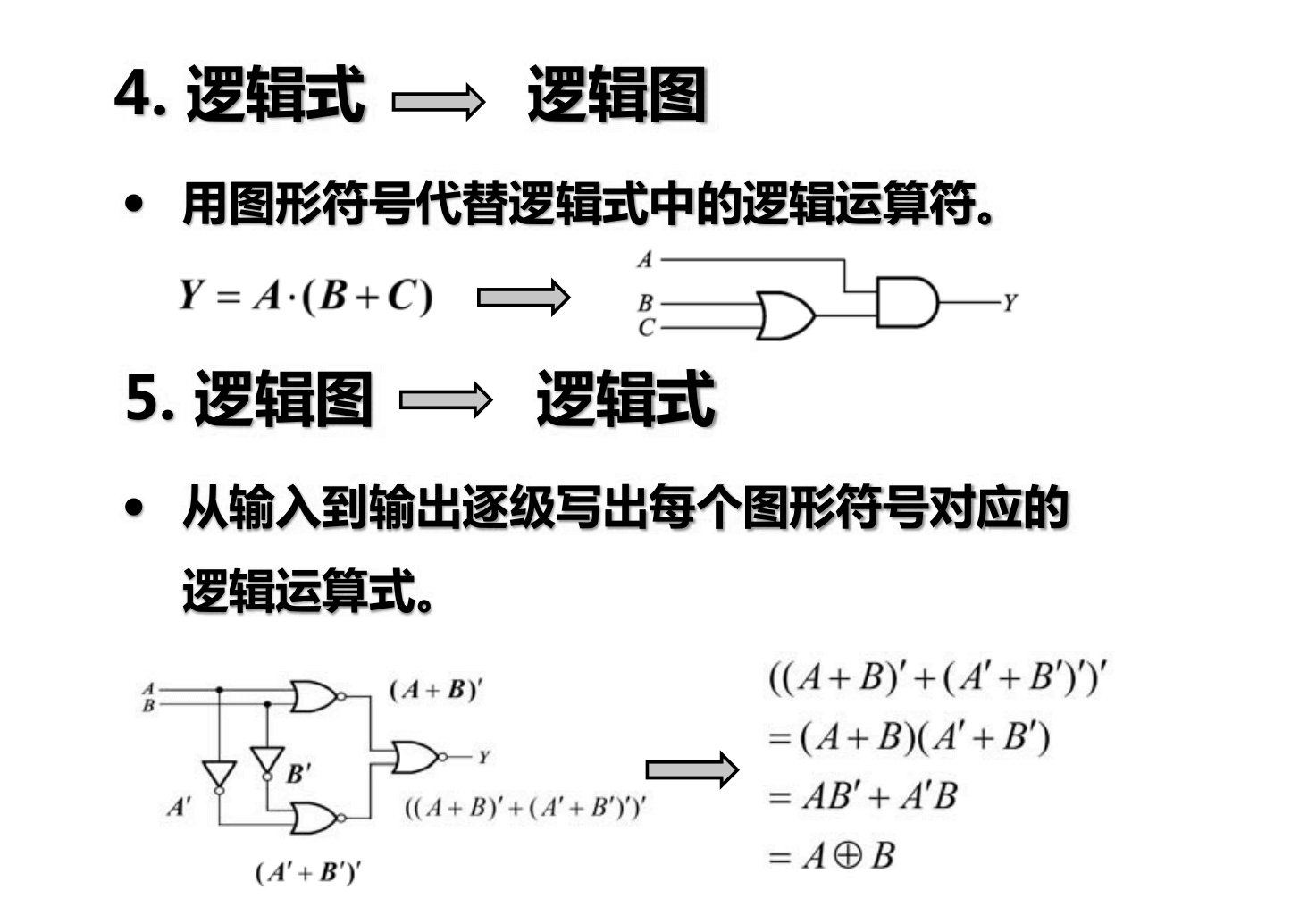
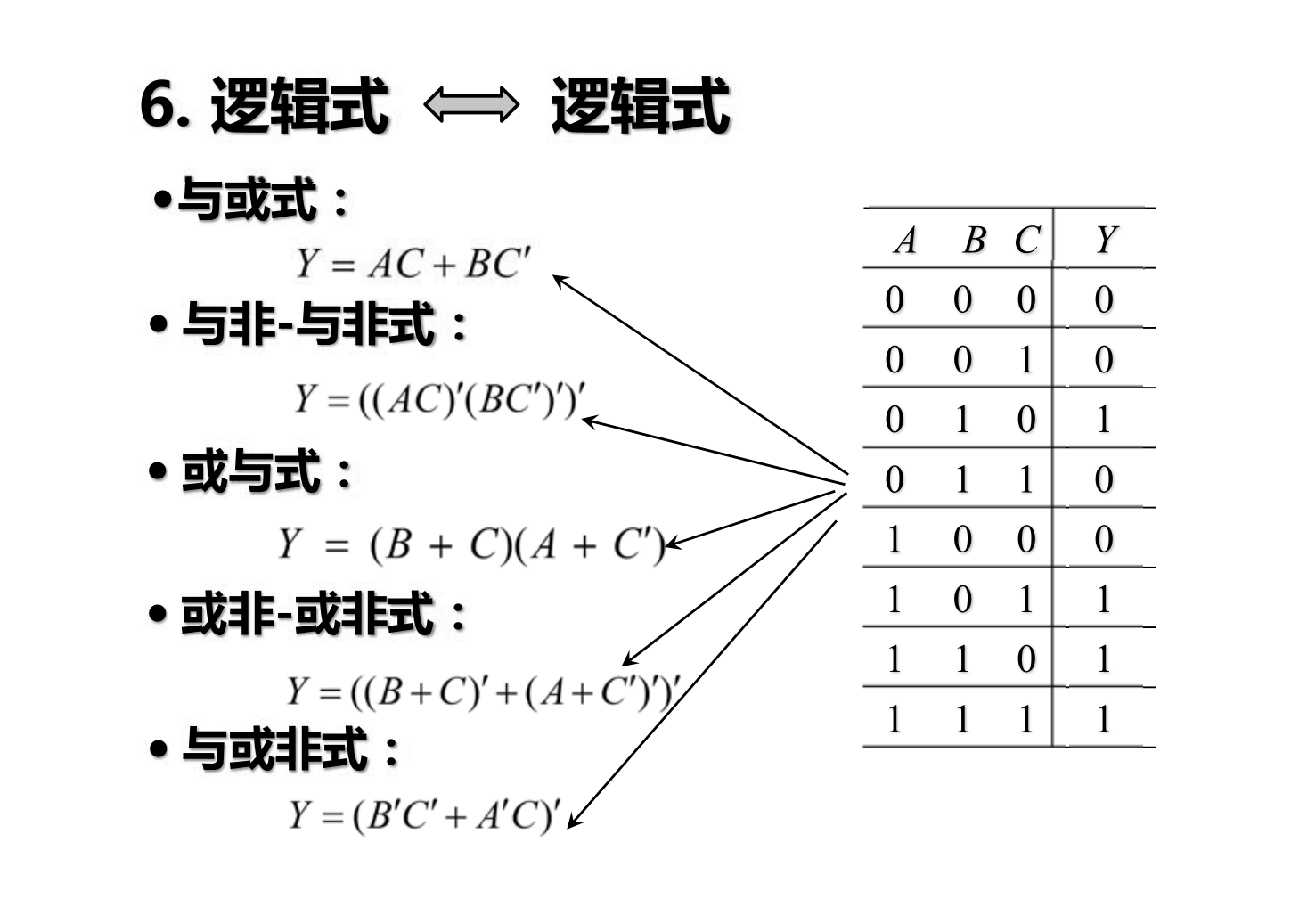
- Expresión lógica
- Diagrama lógico
- Gráfico de forma de onda
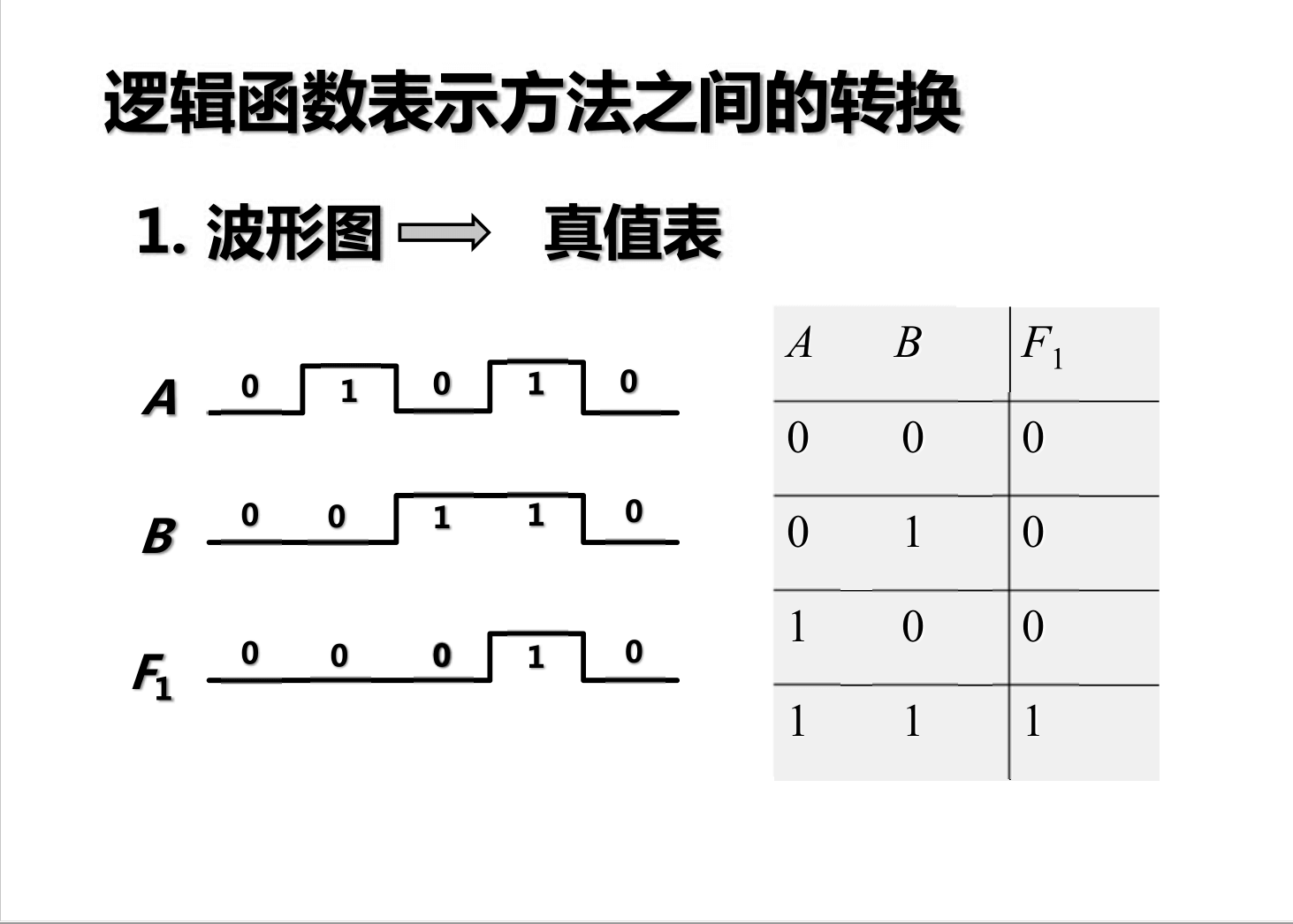
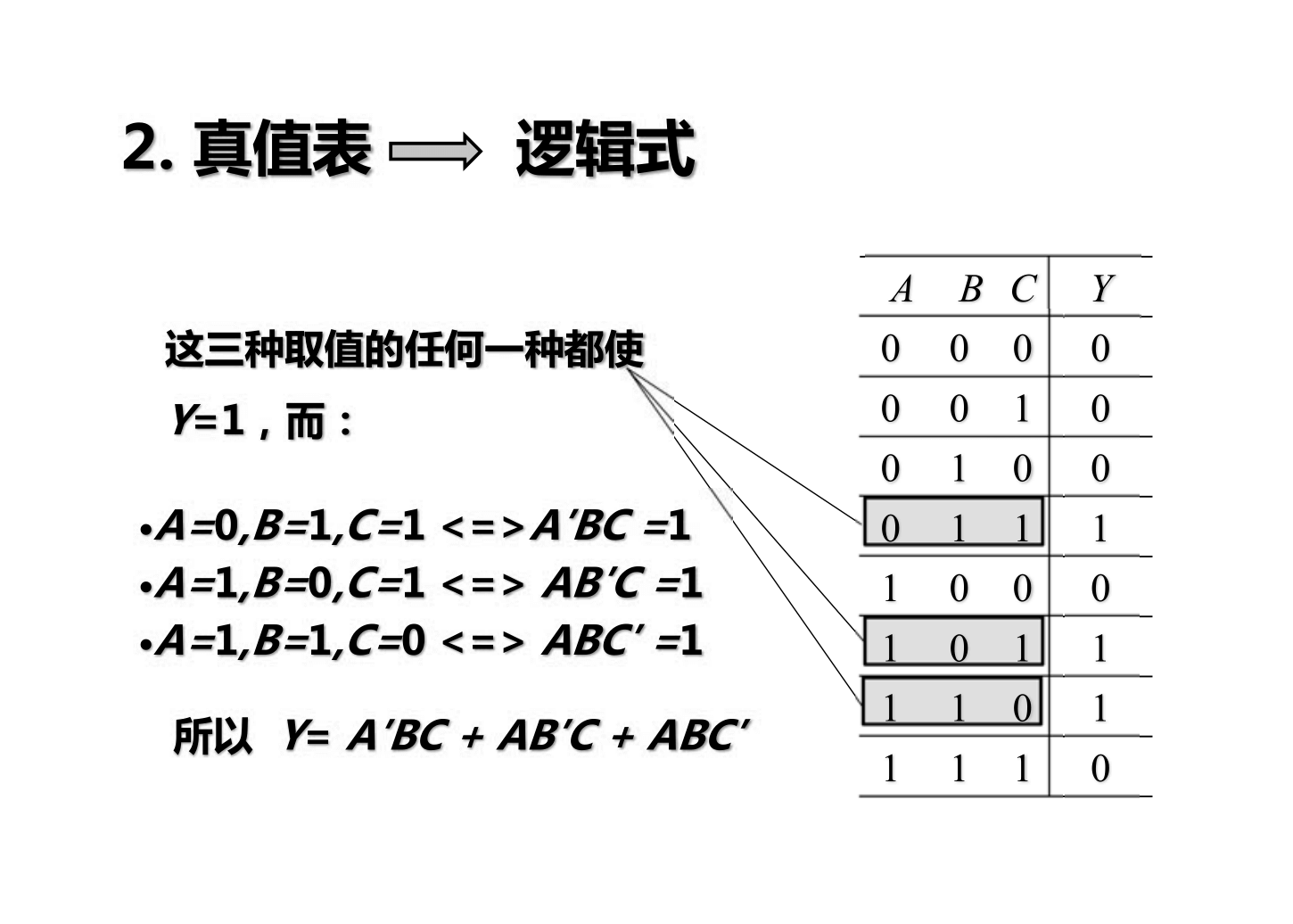

Método de simplificación de funciones lógicas
Forma más simple de una expresión lógica
Términos mínimos
En realidad, son las filas de la tabla de verdad
Representan todas las posibles y únicas situaciones
Método de simplificación de expresiones
Aplicando repetidamente fórmulas básicas y fórmulas comunes, se eliminan los términos redundantes y los factores redundantes. 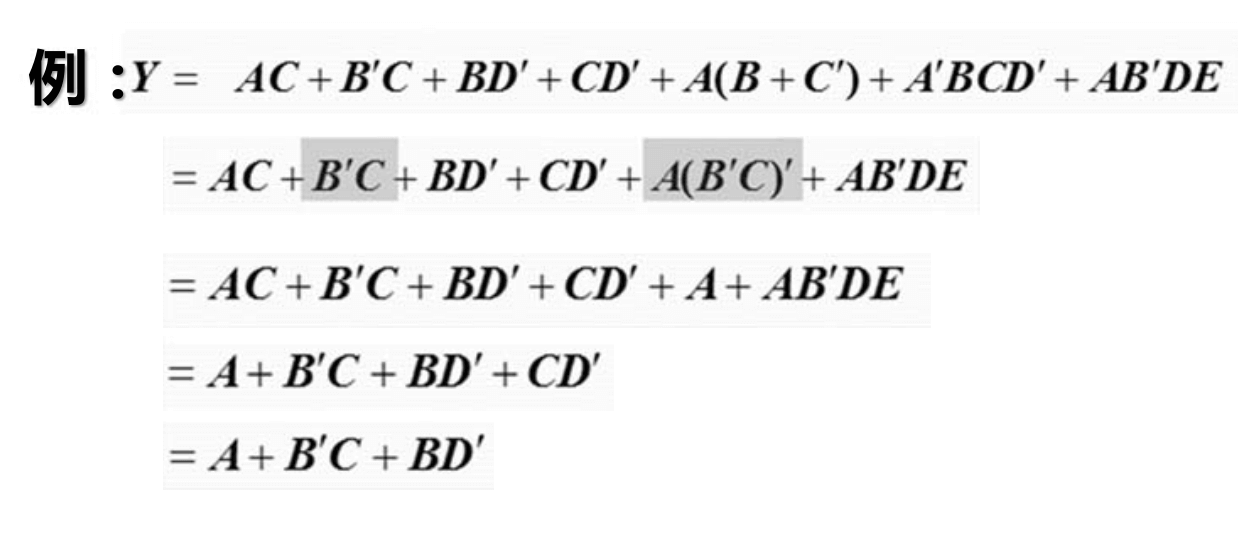
Método de simplificación mediante mapas de Karnaugh
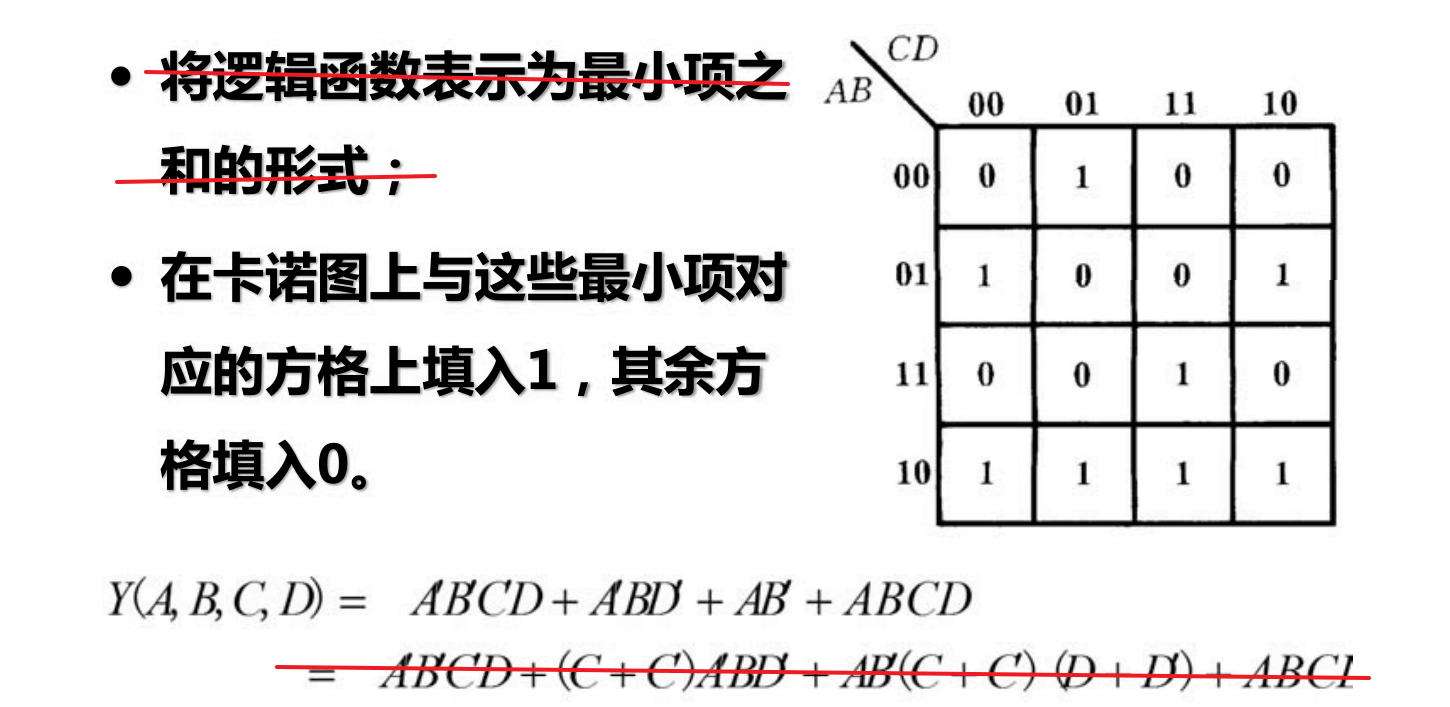
No es necesario convertir todo en términos mínimos.
Si los términos mínimos se repiten, se marca con 1.
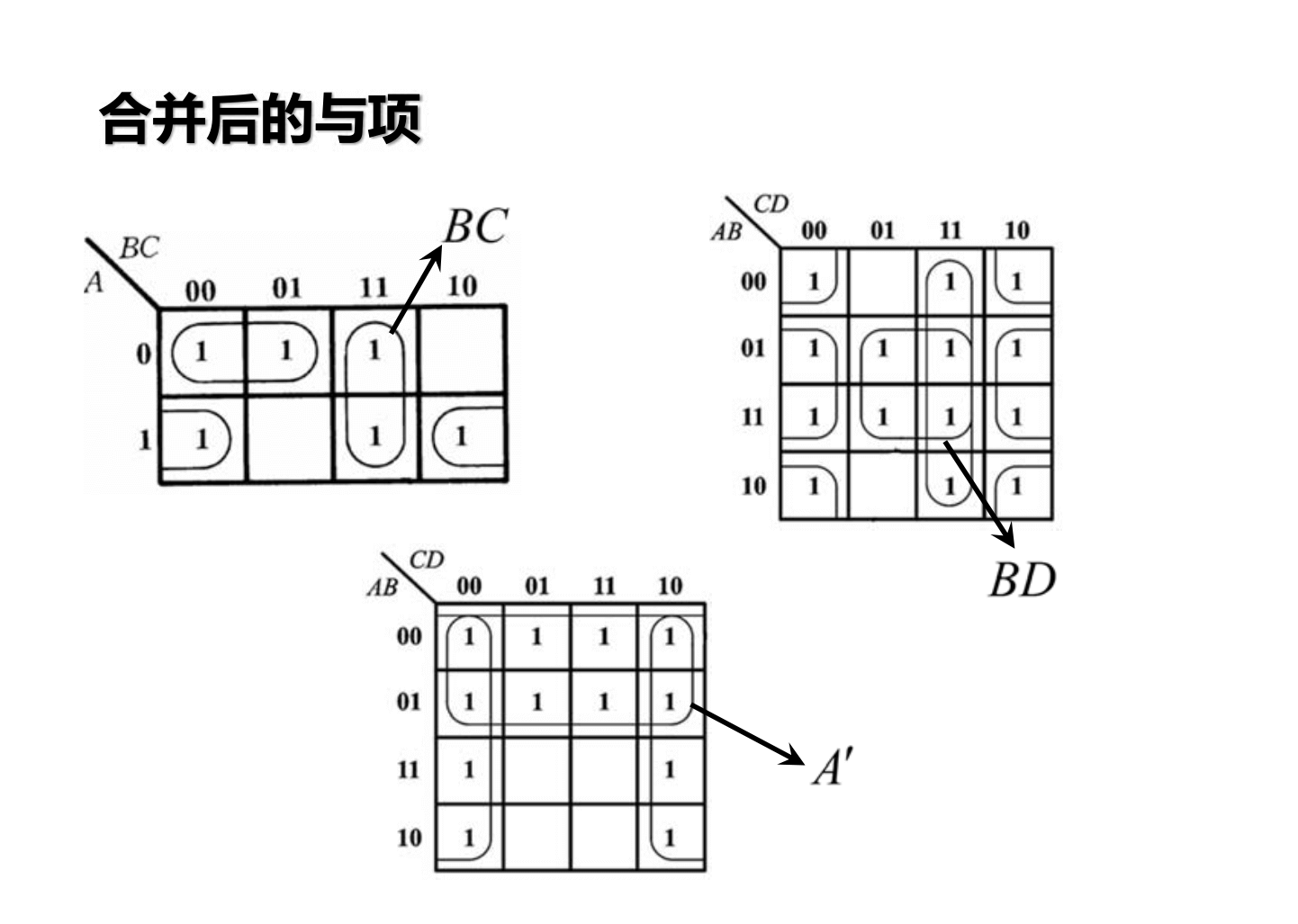
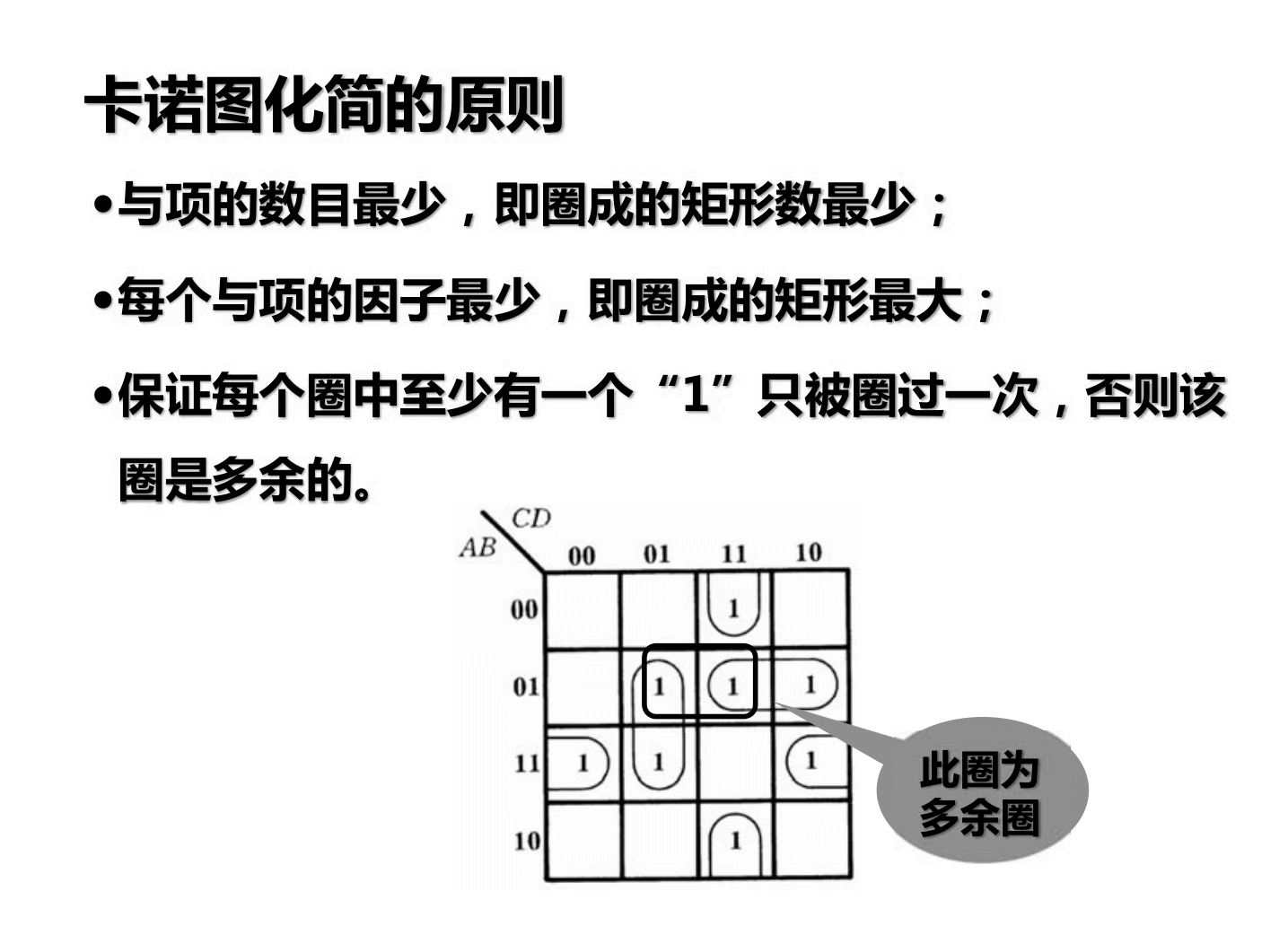
Si hay pocos 0, también se puede rodear el 0 y luego negarlo.
Circuitos lógicos
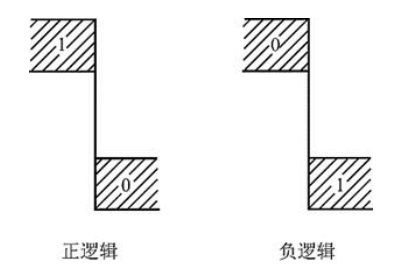
Lógica positiva y lógica negativa
Si se utiliza un nivel alto de voltaje para representar el 1 lógico y un nivel bajo de voltaje para representar el 0 lógico, se denomina lógica positiva; de lo contrario, se denomina lógica negativa.
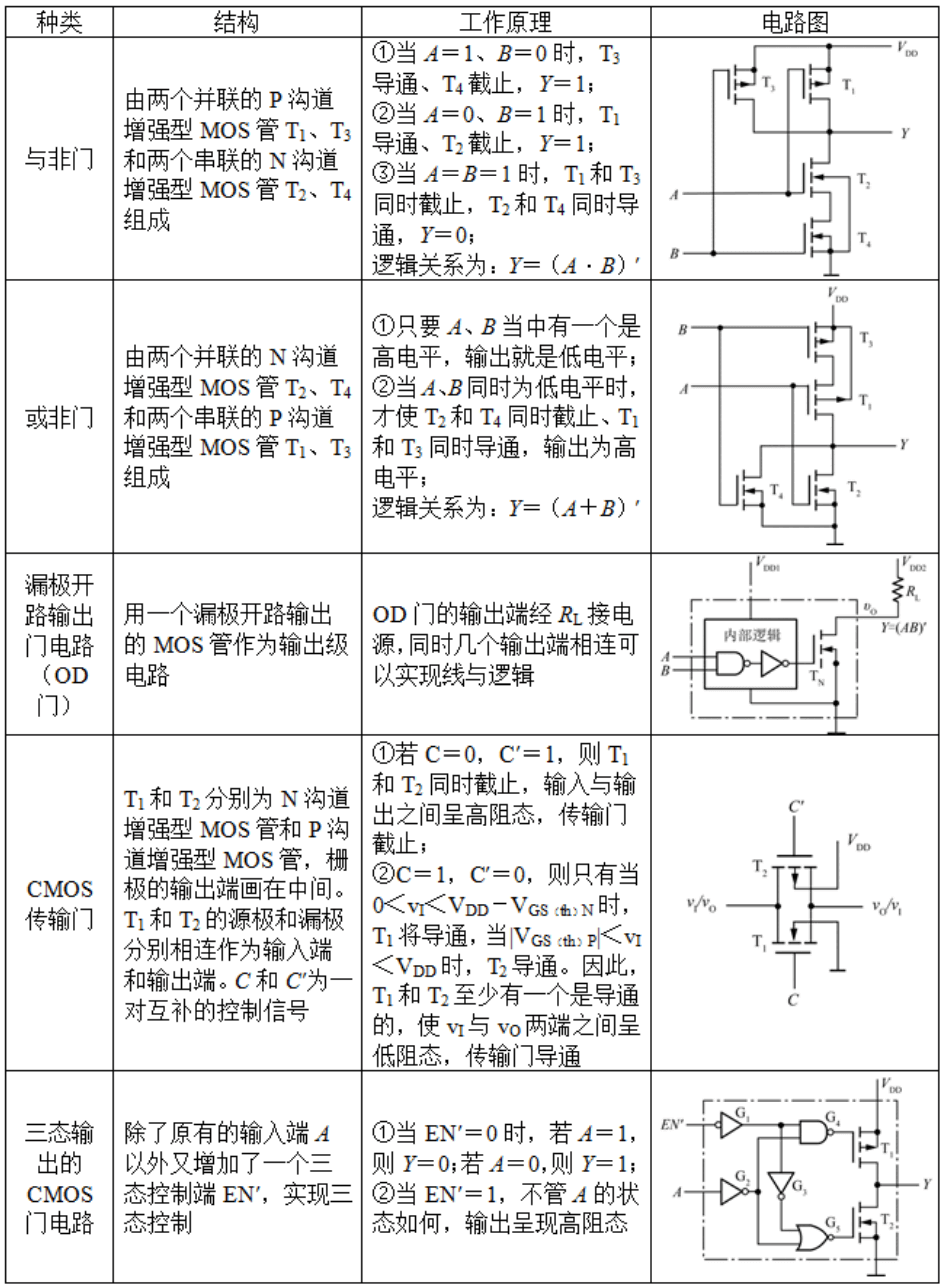
Circuitos de puertas lógicas CMOS
Referencias y agradecimientos
- "Codificación: El lenguaje oculto detrás del hardware y software de computadoras"
Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.