Radiofrecuencia - Circuitos resonantes - Definición básica
En este capítulo, estudiaremos los circuitos resonantes en paralelo y sus características en radiofrecuencia, el concepto de factor de calidad (Q) y su relación con la impedancia de la fuente y la impedancia de carga, también estudiaremos las pérdidas de los componentes y cómo afectan al circuito, y por último, mostraremos algunos circuitos resonantes acoplados.
Los circuitos resonantes se utilizan en cada transmisor, receptor y equipo de prueba en circuitos de radiofrecuencia para transmitir selectivamente una frecuencia o grupo de frecuencias desde la fuente hasta la carga, al mismo tiempo que atenúan todas las demás frecuencias fuera de la banda de paso. Un circuito resonante ideal se ve así:
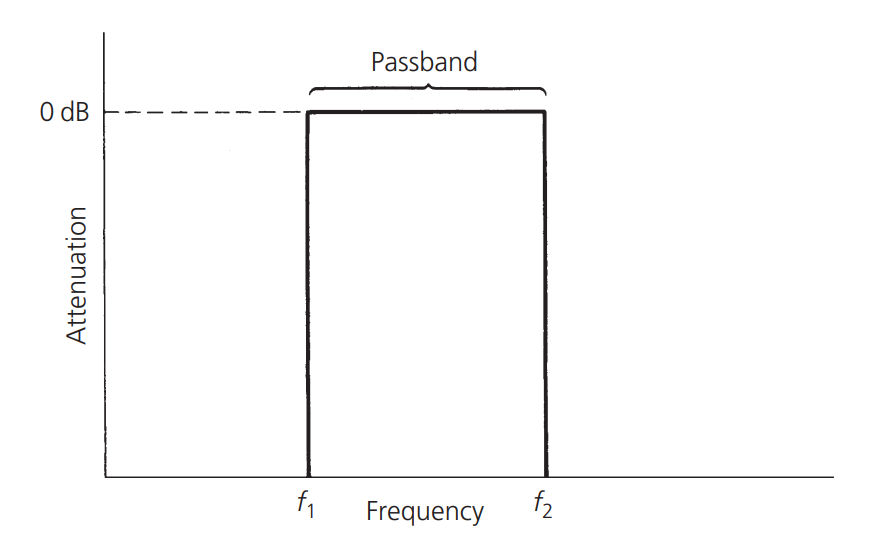
Es una banda de paso rectangular perfecta, con atenuación infinita en frecuencias por debajo o por encima de la banda objetivo, permitiendo que las señales dentro de la banda objetivo pasen sin interferencias. Sin embargo, debido a las propiedades físicas de los componentes que forman el filtro, un filtro perfecto es imposible, pero podemos diseñar filtros no ideales que cumplan con los requisitos.
Ancho de banda
El ancho de banda (Bandwidth) generalmente se refiere al ancho de banda de media potencia, es decir, la diferencia entre las frecuencias límite superior e inferior en las que la respuesta de amplitud está 3 dB por debajo de la respuesta de banda pasante, como se muestra en la siguiente imagen:
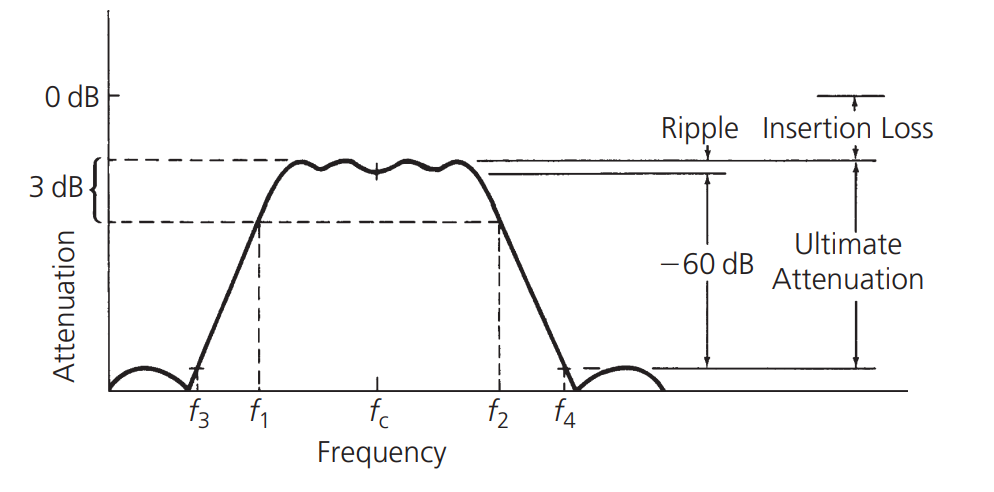
Significado y cálculo de dB
dB es un valor relativo que puede representar de manera concisa números muy grandes o muy pequeños. Por ejemplo, si queremos representar un aumento de potencia de 100000000 veces, solo necesitamos escribir +80 dB.
Donde \(P_1\) representa la potencia actual y \(P_0\) representa la potencia de referencia. Si \(P_1\) es el doble de \(P_0\), entonces:
Si \(P_1\) es la mitad de \(P_0\), entonces:
De manera similar, +10 dB representa un aumento de potencia de 10 veces, -10 dB representa una disminución de potencia a 1/10.
El valor de 3 dB se encuentra frecuentemente en gráficos de potencia o gráficos de tasa de error, donde +3 dB significa duplicar la potencia y -3 dB significa reducir a la mitad la potencia.
dBm y dBw
dBm y dBw son formas de expresar la potencia en dB utilizando como referencia 1 mW y 1 W, respectivamente:
Dado que 1 mW y 1 W son valores fijos, dBm y dBw pueden representar el valor absoluto de la potencia.
Aquí hay una tabla de conversión entre la potencia actual y los valores en dBm y dBw:
| watt | dBm | dBw |
|---|---|---|
| 0.1 pW | -100 dBm | -130 dBW |
| 1 pW | -90 dBm | -120 dBW |
| 10 pW | -80 dBm | -110 dBW |
| 100 pW | -70 dBm | -100 dBW |
| 1 nW | -60 dBm | -90 dBW |
| 10 nW | -50 dBm | -80 dBW |
| 100 nW | -40 dBm | -70 dBW |
| 1 μW | -30 dBm | -60 dBW |
| 10 μW | -20 dBm | -50 dBW |
| 100 μW | -10 dBm | -40 dBW |
| 794 μW | -1 dBm | -31 dBW |
| 1.000 mW | 0 dBm | -30 dBW |
| 1.259 mW | 1 dBm | -29 dBW |
| 10 mW | 10 dBm | -20 dBW |
| 100 mW | 20 dBm | -10 dBW |
| 1 W | 30 dBm | 0 dBW |
| 10 W | 40 dBm | 10 dBW |
| 100 W | 50 dBm | 20 dBW |
| 1 kW | 60 dBm | 30 dBW |
| 10 kW | 70 dBm | 40 dBW |
| 100 kW | 80 dBm | 50 dBW |
| 1 MW | 90 dBm | 60 dBW |
| 10 MW | 100 dBm | 70 dBW |
Entre ellos, el más comúnmente utilizado es 1 W = 30 dBm.
dBi, dBd y dBc
Los cálculos de dBi, dBd y dBc son similares a los de dB, y representan valores relativos de potencia, pero tienen diferentes significados en relación con la referencia de base \(P_0\).
| dBx | Referencia de base |
|---|---|
| dBi (Decibe-Isotrópico) | Antena isotrópica |
| dBd (Decibe-Dipolo) | Antena dipolo |
| dBc (Decibe-Portadora) | Portadora |
Para una ganancia dada, generalmente dBi es 2.15 unidades más grande que dBd, esta diferencia se debe a la diferente directividad de las dos antenas.
Relación entre la frecuencia central y el ancho de banda de un circuito resonante (Q)
Este Q es diferente de la definición de Q en el artículo anterior. Q es una medida de la selectividad de un circuito resonante, cuanto mayor sea el valor de Q, más estrecho será el ancho de banda y mayor será la selectividad del circuito resonante. La fórmula de Q se define de la siguiente manera:
Factor de forma (Shape Factor, SF)
El factor de forma de un circuito resonante generalmente se define como la relación entre el ancho de banda de 60 dB del circuito resonante y el ancho de banda de 3 dB. Por ejemplo, si el ancho de banda de 60 dB \(f_4 - f_3\) es de 3 MHz y el ancho de banda de 3 dB \(f_2-f_1\) es de 1.5 MHz, entonces el factor de forma es:
El factor de forma es una forma de medir la pendiente de la orilla de la falda. Cuanto menor sea el número, más empinada será la respuesta de la falda. El factor de forma perfecto es 1, que es el valor máximo. Los pasos de banda con un factor de forma menor que 1 se muestran en la siguiente imagen, pero esto no es posible físicamente:
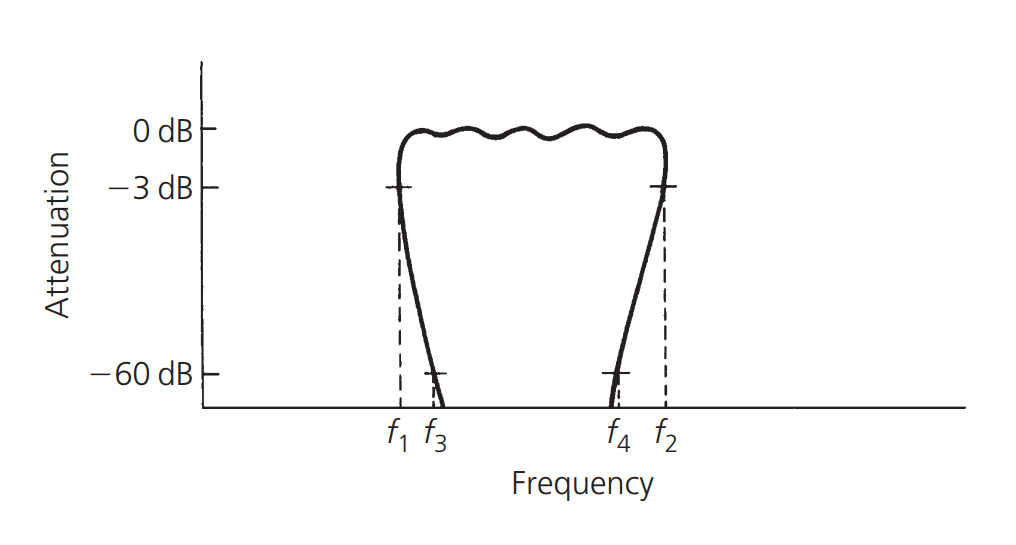
Atenuación máxima (Ultimate attenuation)
Se refiere a la diferencia entre la atenuación máxima en la banda de paso y el pico de atenuación fuera de la banda de paso. Debido a las características físicas reales de los componentes, la atenuación máxima no puede ser infinita.
Pérdida de inserción (Insertion Loss)
Se refiere a la atenuación causada por los componentes entre la fuente de señal y el extremo. En el caso de una falta de coincidencia de impedancia, debido a la resistencia de estos componentes, algunas señales en el extremo de la fuente serán absorbidas por estos componentes, lo que resulta en una atenuación llamada pérdida de inserción, que se expresa en dB.
Ripple (Ripple)
El ripple representa la planitud de la banda de paso de un circuito resonante, y se expresa en dB. Su valor se define como la diferencia entre la atenuación máxima y la atenuación mínima en la banda de paso.
Referencias y agradecimientos
- "RF-Circuit-Design (segunda edición) _Chris-Bowick"
- Comprender las diferencias entre dB, dBm y dBw en 100 minutos
Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.