Conocimientos Básicos de Antenas de Radiofrecuencia
Este artículo tiene como objetivo presentar los principios y parámetros fundamentales de las antenas.
Principios de las Antenas
Una antena es un dispositivo que actúa como un convertidor entre señales eléctricas en un conductor y ondas electromagnéticas en el espacio. Puede transformar las señales eléctricas en ondas de radio y transmitirlas al espacio, o bien captar ondas de radio del espacio y convertirlas en señales eléctricas (aunque las antenas activas son una excepción a este principio).
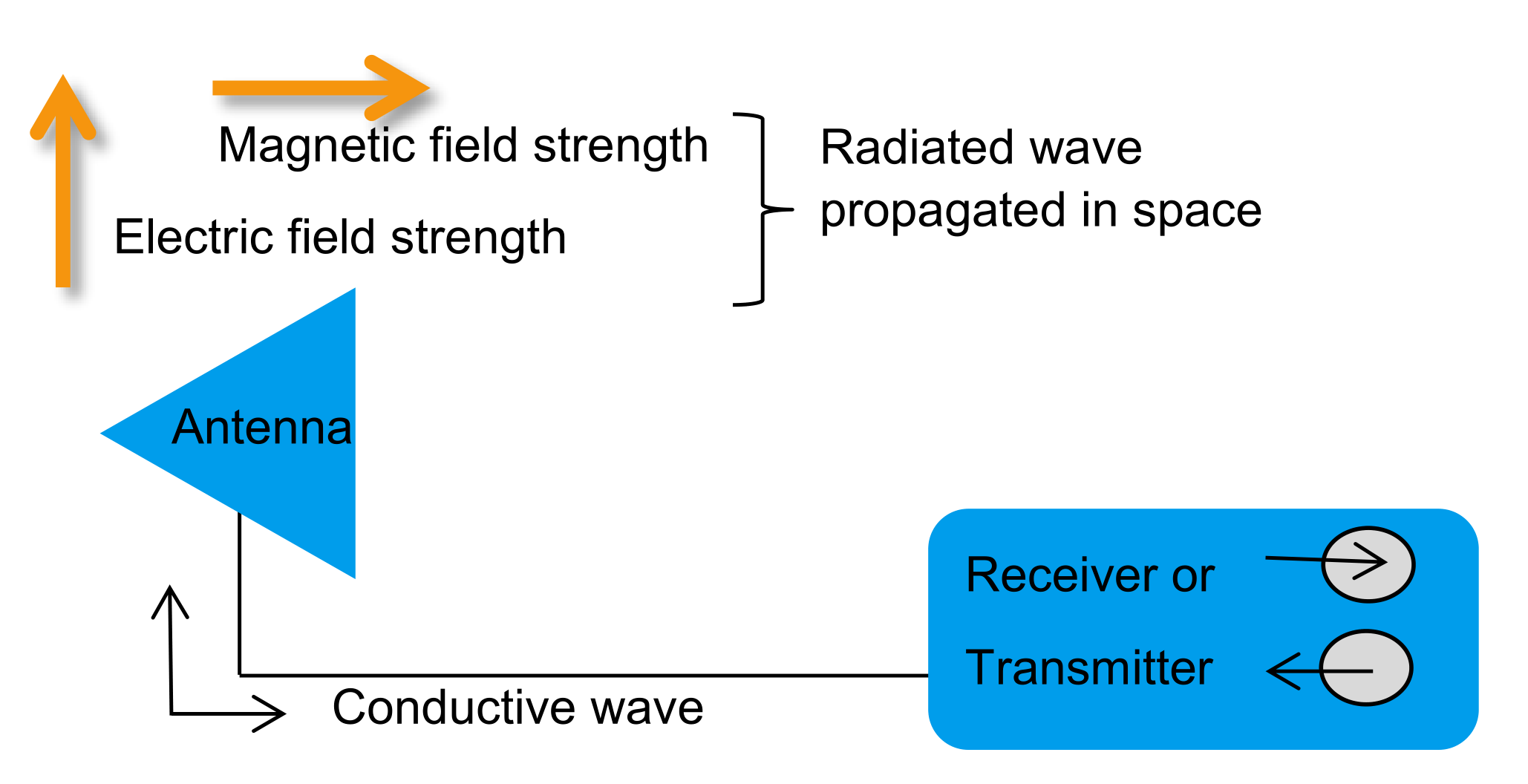
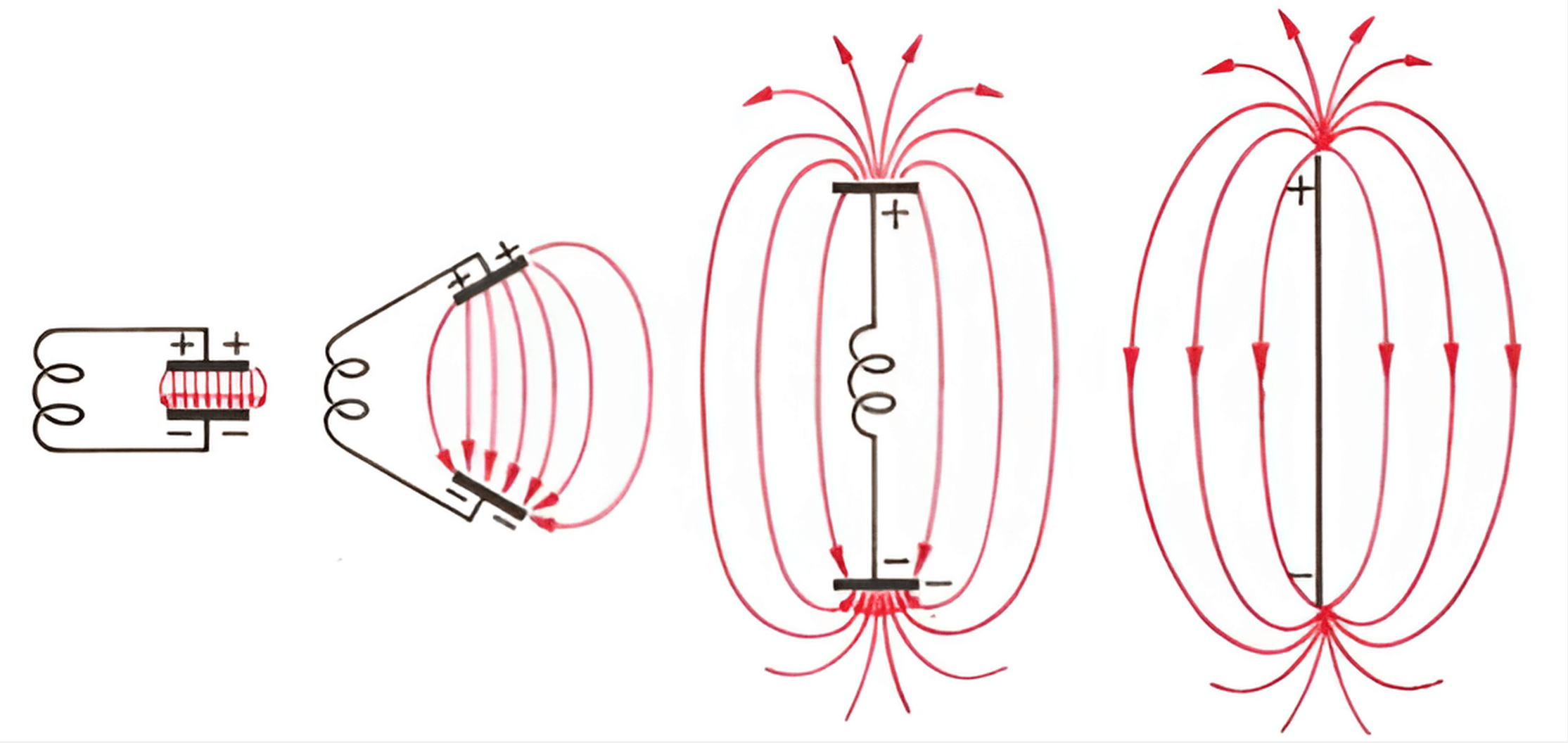
Las antenas se originan a partir de un resonador compuesto por inductancia y un condensador de placas paralelas. Al separar las placas paralelas, la inductancia disminuye. Al separarlas a una distancia específica y considerar la inductancia inherente del conductor, se forma una antena dipolo.
Parámetros de las Antenas
Densidad de Radiación (Radiation Density)
Imaginemos un emisor ideal isotrópico de microondas. Es un punto en el espacio que genera ondas esféricas y distribuye la radiación de manera uniforme en todas las direcciones.
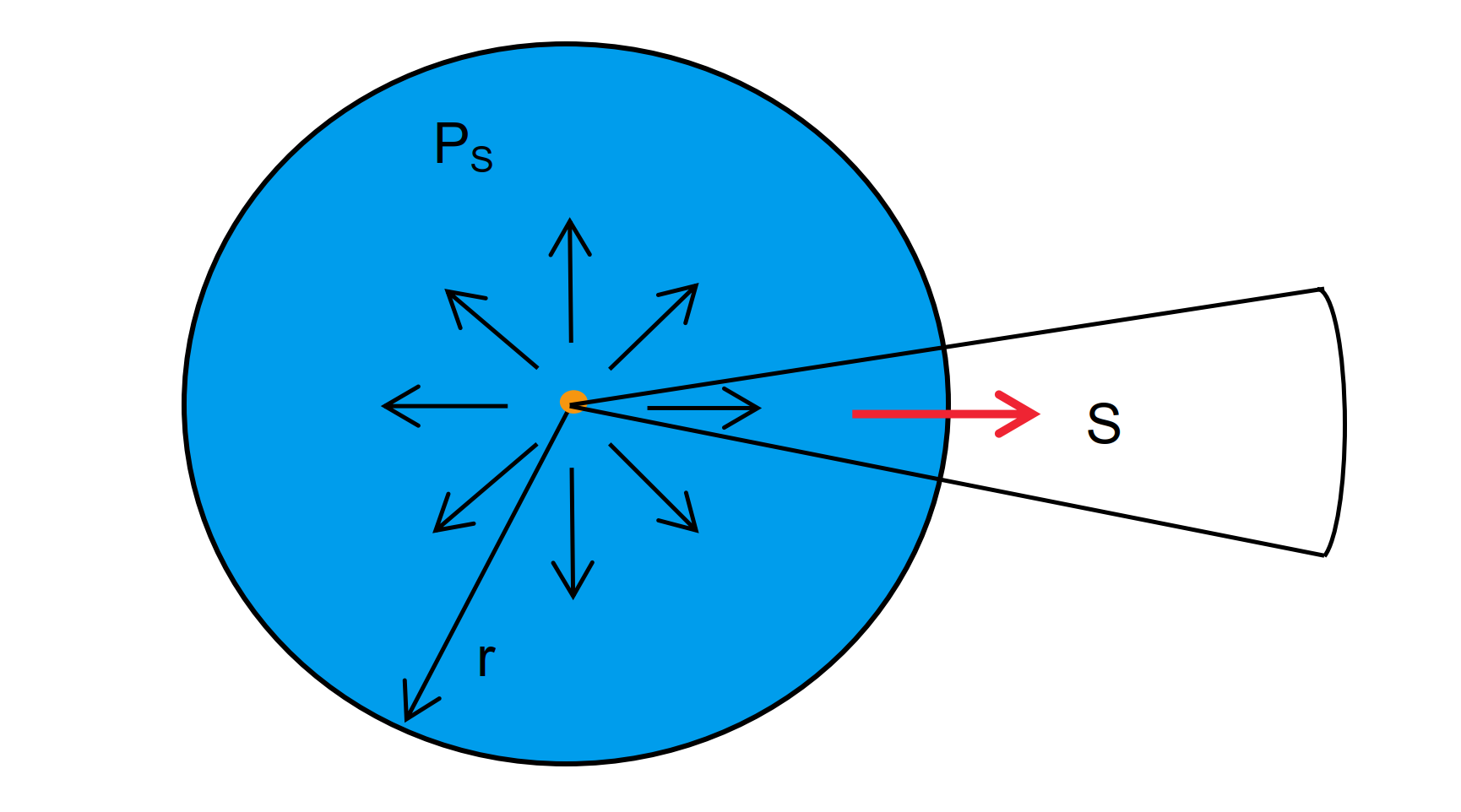
La densidad de radiación (también conocida como densidad de potencia) en un punto a una distancia r del emisor, al aplicar una potencia de transmisión P_S, se calcula de la siguiente manera:
También se puede definir la densidad de radiación como el producto de los campos eléctrico y magnético en el campo lejano:
Patrón de Radiación (Radiation Pattern)
El patrón de radiación se utiliza para describir cómo una antena irradia energía en el espacio en tres dimensiones en el campo lejano. Para un generador isotrópico de radiación (llamado antena puntual), la magnitud de la radiación es igual en todas las direcciones, pero no tiene polarización en una dirección específica. Por ejemplo, el patrón de radiación 3D de una antena de dipolo corto en el espacio libre se muestra en la siguiente figura. Se observa que no hay radiación en la dirección del eje de la antena:
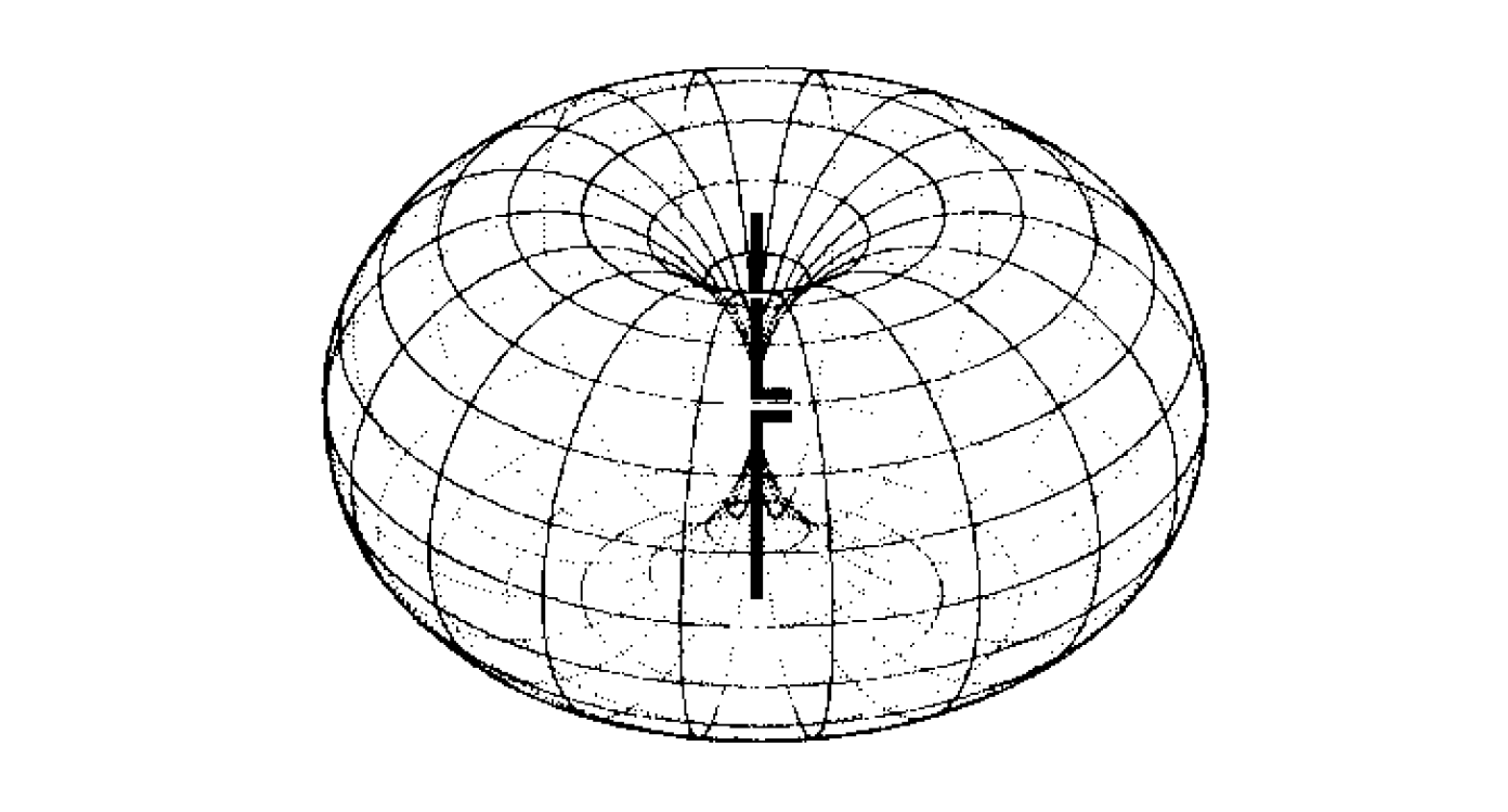
Además de representar el patrón de radiación en 3D, a menudo se utilizan gráficos bidimensionales (también llamados diagramas de plano principal) que muestran el patrón de radiación en los planos horizontal y vertical, respectivamente. Aquí tienes los diagramas de plano principal de una antena de dipolo:
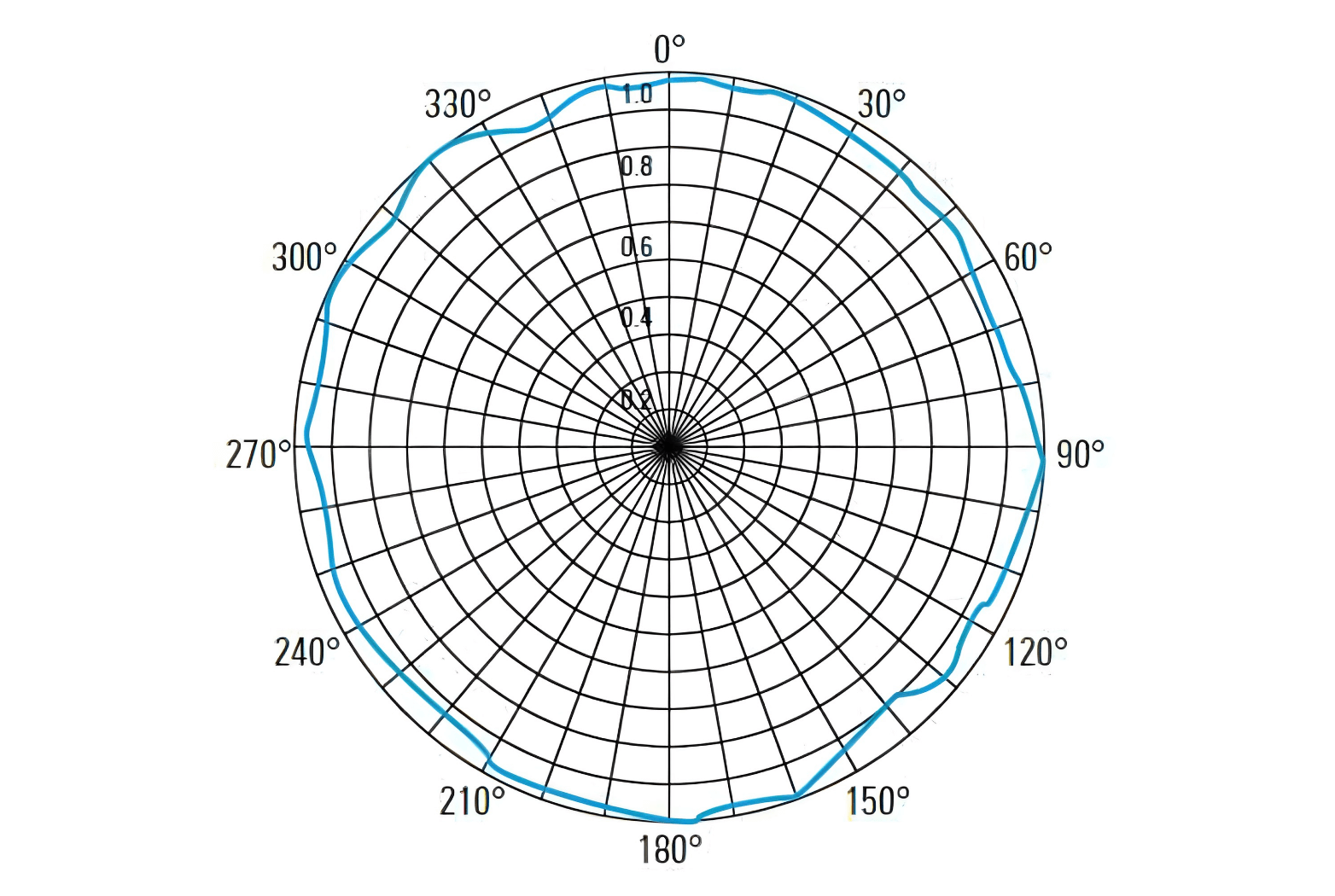
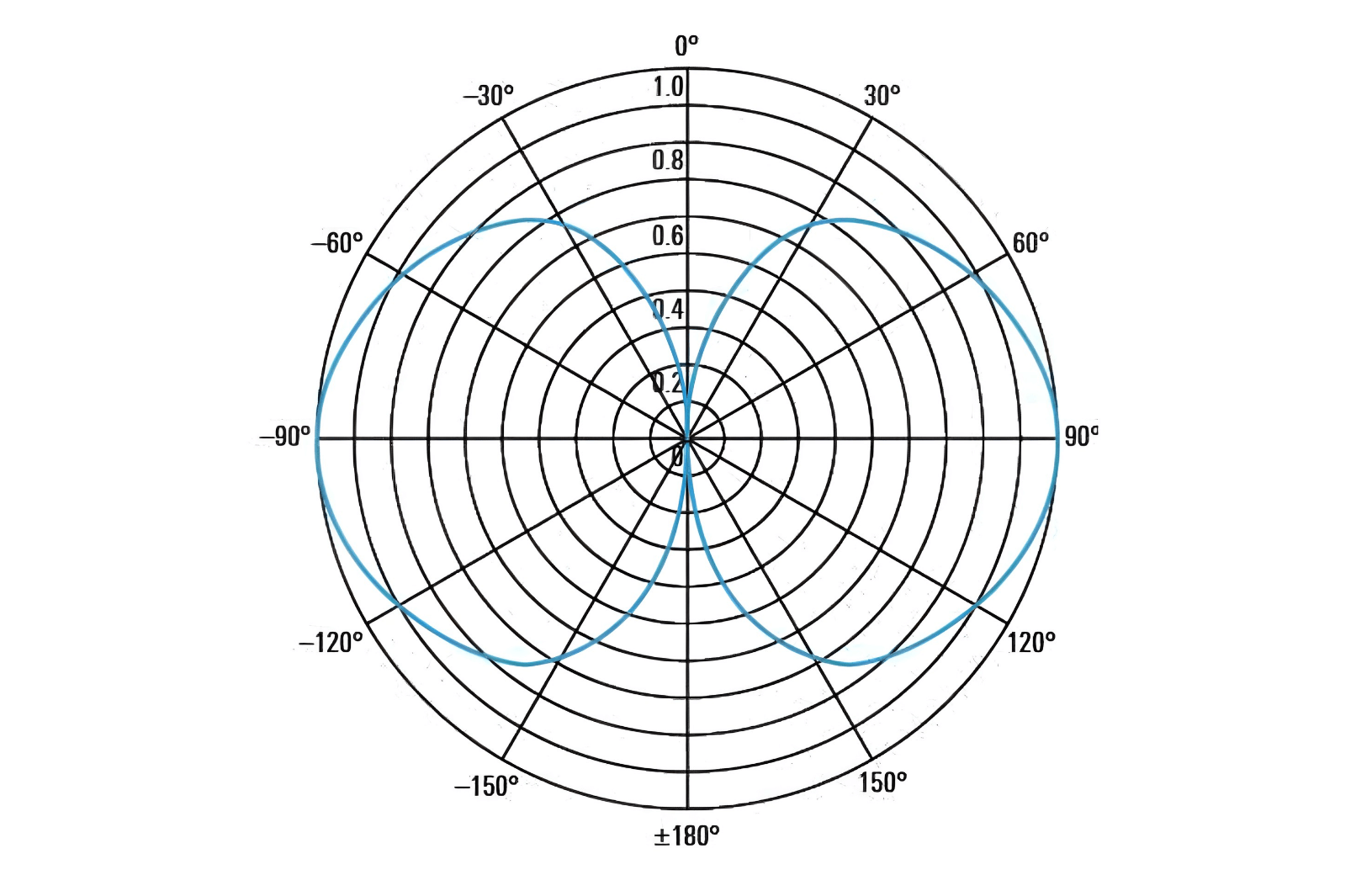
Los patrones de radiación suelen representarse en coordenadas polares para visualizar mejor la distribución de energía en diferentes direcciones. En algunos casos, como en antenas altamente direccionales, se representan en coordenadas cartesianas (sistema X-Y) para resaltar claramente los detalles del lóbulo principal y los lóbulos secundarios:
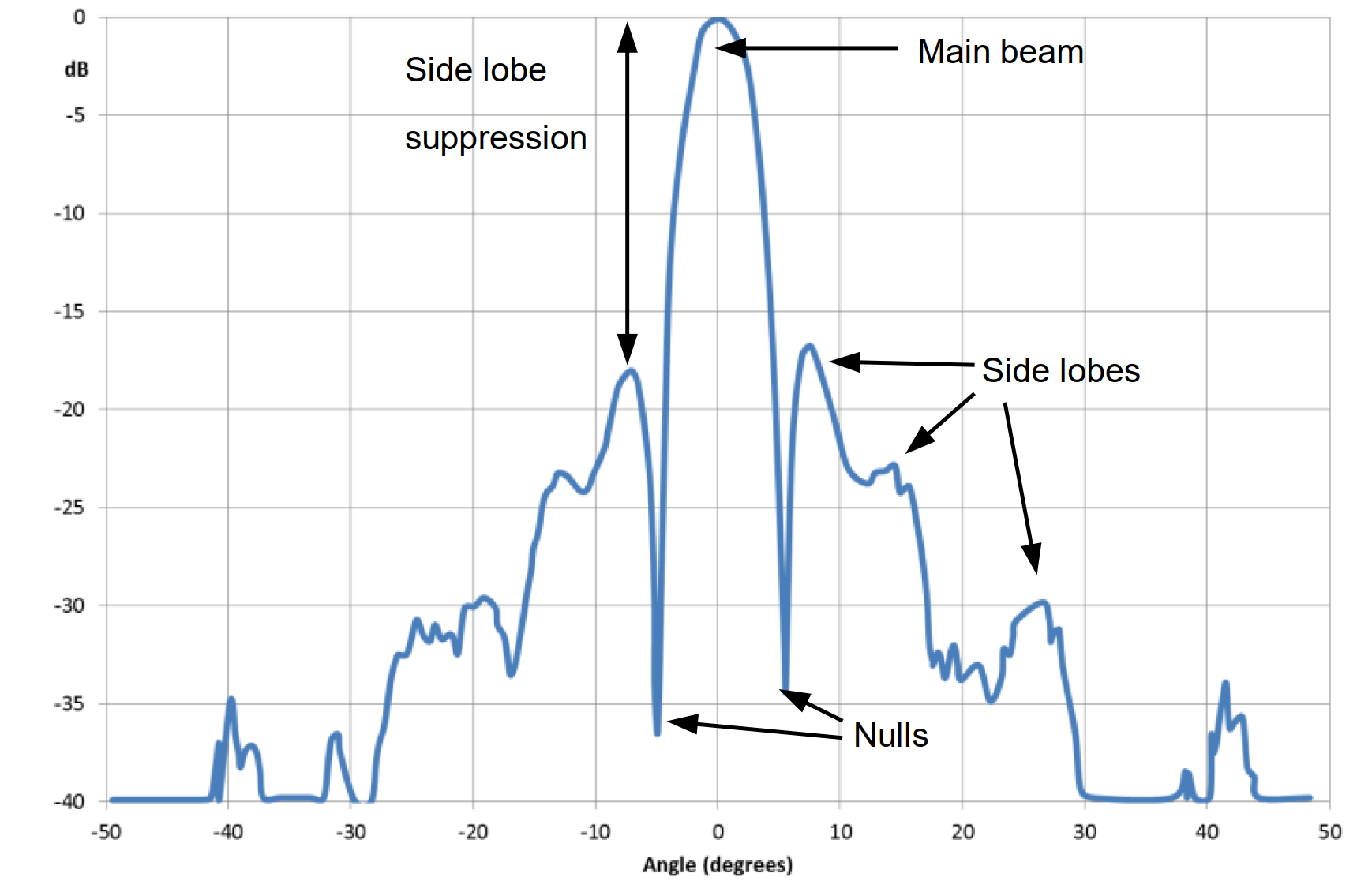
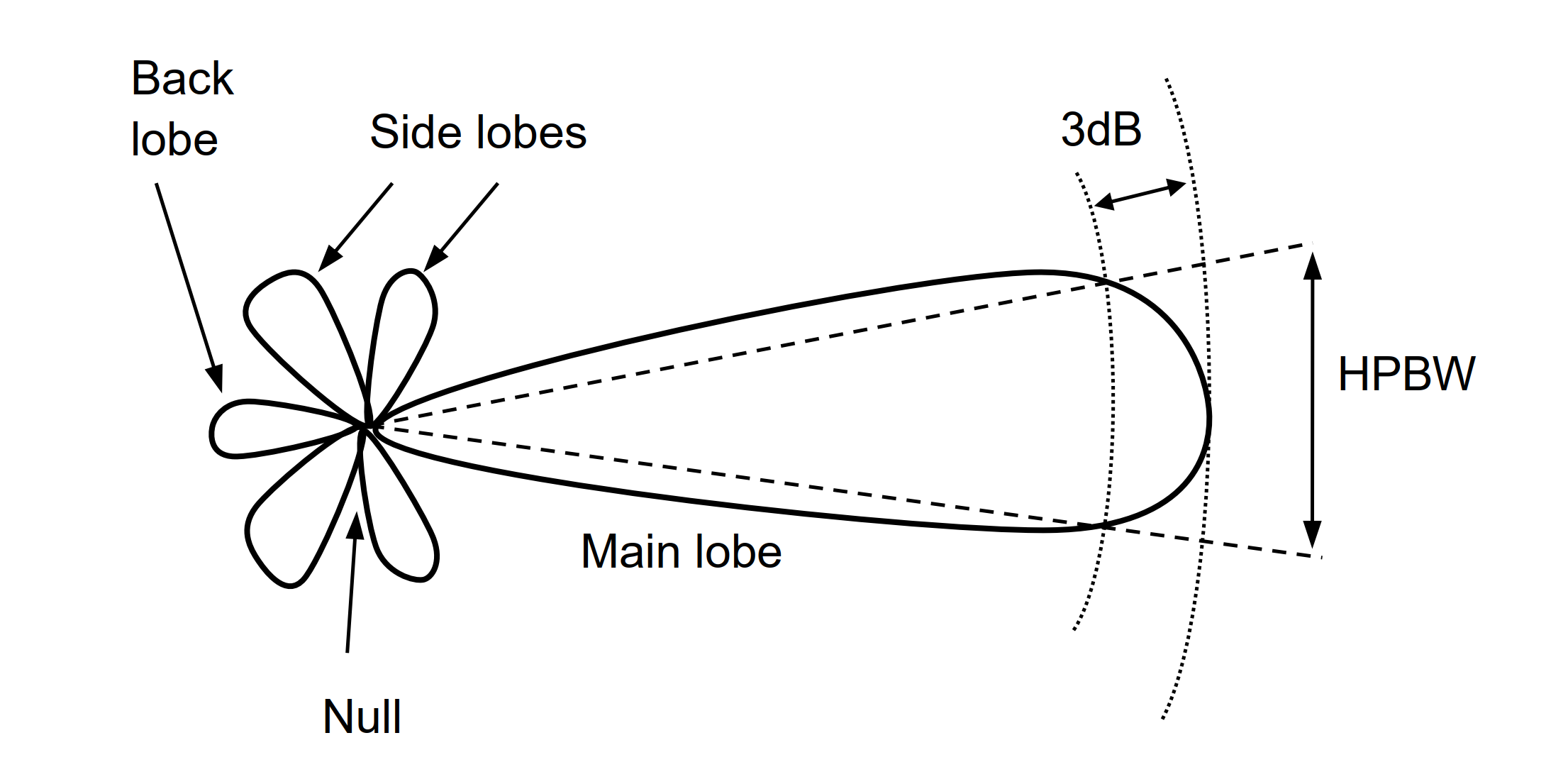
A partir del patrón de radiación, se pueden deducir varios parámetros de la antena:
- Supresión de Lóbulos Secundarios (Side Lobe Suppression o Side Lobe Level): Indica la diferencia entre el lóbulo principal y el lóbulo secundario más alto.
- Ancho del Haz a la Mitad de la Potencia (Half-Power Beamwidth, HPBW): Representa el rango de ángulos a izquierda y derecha del lóbulo principal donde la ganancia disminuye 3 dB desde su máximo. Generalmente se muestra en los diagramas de patrones de radiación en los planos horizontal y vertical.
- Relación de Frente a Espalda (Front-to-Back Ratio): Indica la relación entre la ganancia máxima de la antena en la dirección frontal y la ganancia en la dirección trasera (180°). Por lo general, se expresa en decibelios (dB).
Directividad
El factor de directividad \(D\) de una antena, también conocido como coeficiente de directividad, representa la intensidad de radiación en la dirección principal de la antena \(F_{max}\) en comparación con la intensidad de radiación de una antena puntual sin pérdida con la misma potencia total (\(P_t\)). Aquí, utilizamos el vector de Poynting para representar la densidad de potencia en lugar de la intensidad de radiación:
**Nota**: En el campo lejano, $\vec S$ es perpendicular a $\vec E$, y tanto $\vec S$ como $\vec E$ son perpendiculares a $\vec H$.
La densidad de potencia se mide a una distancia $r$ igual a la distancia de la antena, por lo tanto, cuando $F_i = \frac{P_t}{4\pi}$, podemos obtener:
$$
D = \frac{F_{max}}{F_i}
$$
### Eficiencia (Efficiency)
La eficiencia de la antena $\eta$ generalmente se define como la relación entre la potencia radiada de la antena y la potencia de entrada. Las antenas de alta eficiencia pueden irradiar la mayor parte de la energía de entrada, mientras que las antenas de baja eficiencia absorben la mayor parte de la energía como pérdidas internas de la antena o la reflejan debido a desajustes de impedancia. Para antenas pasivas, ya sea como antenas de transmisión o recepción, su eficiencia es la misma, y esto se conoce como reciprocidad de la antena (Antenna Reciprocity). La fórmula de eficiencia de radiación de la antena $\varepsilon_R$ se expresa de la siguiente manera:
$$
\varepsilon_R = \frac{P_{refl}}{P_{forw}} \cdot 100\%
$$
La eficiencia de la antena se expresa no solo en porcentaje, sino también en decibelios (dB). Por ejemplo, una eficiencia del 10% es equivalente a -10 dB, y una eficiencia del 50% es equivalente a -3 dB.
Las fórmulas anteriores representan la eficiencia de radiación de la antena, pero también existe otro tipo de eficiencia llamada eficiencia total de la antena \(\varepsilon_r\). La relación entre ellas es que la eficiencia total es igual a la eficiencia de radiación multiplicada por la pérdida de coincidencia de impedancia \(M_L\):
Dado que la pérdida de coincidencia de impedancia se encuentra entre 0 y 1, la eficiencia total de la antena siempre será menor que la eficiencia de radiación. Si la coincidencia de impedancia es perfecta, ambas eficiencias serán iguales. En la práctica, la eficiencia de la antena suele referirse a la eficiencia total considerando las pérdidas de coincidencia de impedancia, por lo tanto, un mejor ajuste de impedancia puede mejorar la eficiencia real de la antena.
Ganancia (Gain)
La ganancia de la antena se utiliza para medir la capacidad de la antena para transmitir o recibir señales en una dirección específica. La ganancia está estrechamente relacionada con el patrón de radiación de la antena: cuanto más estrecho sea el haz principal del patrón de radiación y menor sean los lóbulos secundarios, mayor será la ganancia.
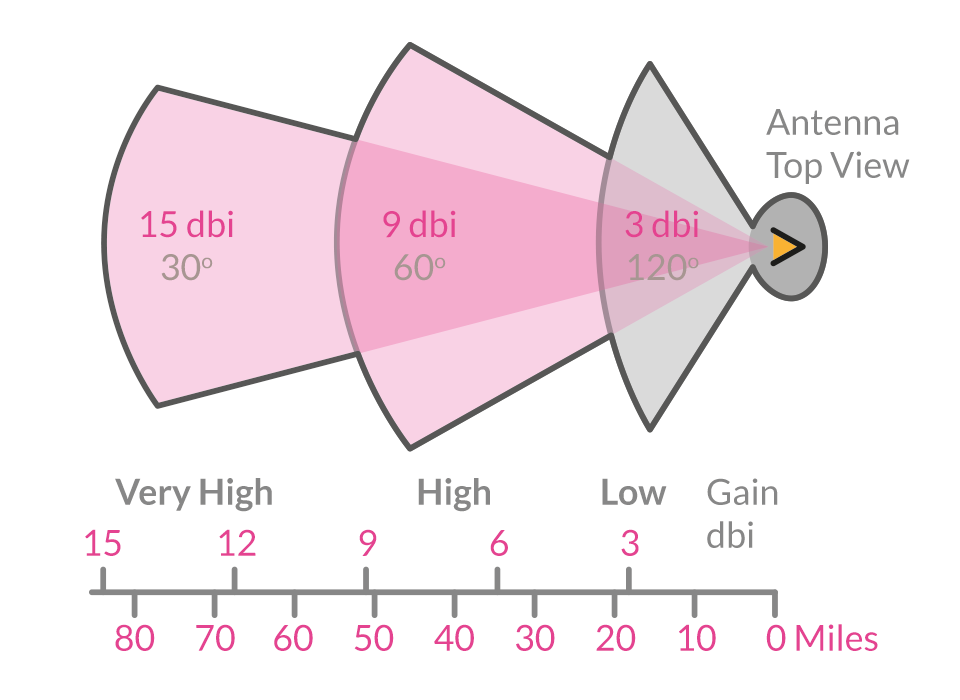
En las mismas condiciones, una mayor ganancia implica una mayor concentración de energía, un haz más estrecho y una mayor distancia de propagación de ondas electromagnéticas, pero con un ángulo de cobertura más pequeño. Por lo tanto, en la práctica, se debe elegir la ganancia de la antena de manera adecuada.
La ganancia de la antena corresponde al coeficiente de dirección, que representa la intensidad de radiación en la dirección principal \(F_{max}\) en comparación con la intensidad de radiación producida por una antena puntual sin pérdidas (\(F_{i0}=\frac{P_t}{4\pi}\)). De esta forma, se obtiene:
A diferencia del coeficiente de dirección, la ganancia también tiene en cuenta la eficiencia de la antena \(\eta\):
Si la eficiencia de la antena es del 100%, la ganancia y el coeficiente de dirección serán iguales, pero en la realidad, la eficiencia no puede alcanzar el 100%, por lo que en las mediciones prácticas, la ganancia es más común que el coeficiente de dirección.
Tanto la ganancia como el coeficiente de dirección se expresan generalmente en decibelios, donde la ganancia \(g(dB) = 10 \log_{10} G\) y el coeficiente de dirección \(d(dB) = 10 \log_{10} D\). Esto da lugar a las unidades dBd (en relación con una antena dipolo de media onda) y dBi (en relación con una antena puntual), y su relación es dBi = dBd + 2.15.
Algunas observaciones adicionales sobre la ganancia:
- Las antenas son dispositivos pasivos y no generan energía. La ganancia de la antena es simplemente su capacidad para concentrar eficazmente la energía en una dirección específica para irradiar o recibir ondas electromagnéticas.
- La ganancia de la antena aumenta a medida que se superponen más elementos radiantes. Cuanto mayor sea la ganancia, mayor será la longitud de la antena. Cada aumento de 3 dB en la ganancia duplica el volumen.
Ganancia Práctica (Practical Gain)
La definición de ganancia presupone una coincidencia perfecta de impedancia entre la antena y la fuente, pero esto rara vez se logra en la práctica. Por lo tanto, la ganancia medida con una coincidencia no ideal se denomina ganancia práctica de la antena. Su fórmula se define de la siguiente manera:
Donde \(r\) representa el coeficiente de reflexión, como se detalla a continuación.
Área Efectiva (Effective Area)
El área efectiva de la antena \(A_W\) es un parámetro específico para las antenas receptoras y mide la capacidad de la antena para captar señales. Se define como la relación entre la máxima potencia recibida \(P{rmax}\) y la densidad de potencia de onda plana \(S\):
Para antenas como reflectores parabólicos o matrices planas, el área efectiva es el producto del área física por la eficiencia
$$
A_W=A_g\cdot q
$$
La superficie efectiva de la antena también está relacionada con la ganancia (mutuamente proporcional):
$$
A_W=\frac{\lambda ^2}{4\pi}\cdot G
$$
### Impedancia de Entrada (Input Impedance)
La impedancia de entrada de la antena es un parámetro crítico que consiste en una parte real (resistencia) y una parte imaginaria (reactancia):
$$
Z_{in}=R_{in}+jX_{in}
$$
La resistencia real, $R_{in$, se compone de la resistencia de radiación $R_R$ y la resistencia de pérdida $R_L$:
$$
R_{in}=R_R+R_L
$$
Para antenas pequeñas, calcular la resistencia de radiación $R_R$ requiere especificar su posición en la antena, ya que es espacialmente dependiente (cociente de la potencia radiada y la raíz cuadrada de la corriente de la antena). Lo mismo se aplica a la corriente de la antena, donde es necesario especificar el punto de alimentación de la antena para determinar el valor máximo de corriente.
Si la antena opera en estado de resonancia, la parte imaginaria de la impedancia de entrada es 0. Las antenas lineales cortas suelen ser capacitivas ($X_{in}<0$), mientras que las antenas lineales largas suelen ser inductivas ($X_{in}>0$).
### Impedancia Nominal (Nominal Impedance)
La impedancia nominal, $Z_n$, generalmente se especifica como la impedancia característica de la línea de conexión de la antena, típicamente 50Ω. Normalmente, la impedancia de la antena debe coincidir con esta.
### Coincidencia de Impedancia (Impedance Matching)
Si las impedancias de la antena, la línea de conexión y el extremo fuente no coinciden, se producirán discontinuidades. En el ejemplo de la imagen a continuación, parte de la energía emitida desde la fuente se refleja y no llega a la antena, lo que afecta la eficacia de la transmisión; de manera similar, la energía recibida desde la antena no se puede transmitir completamente al receptor:
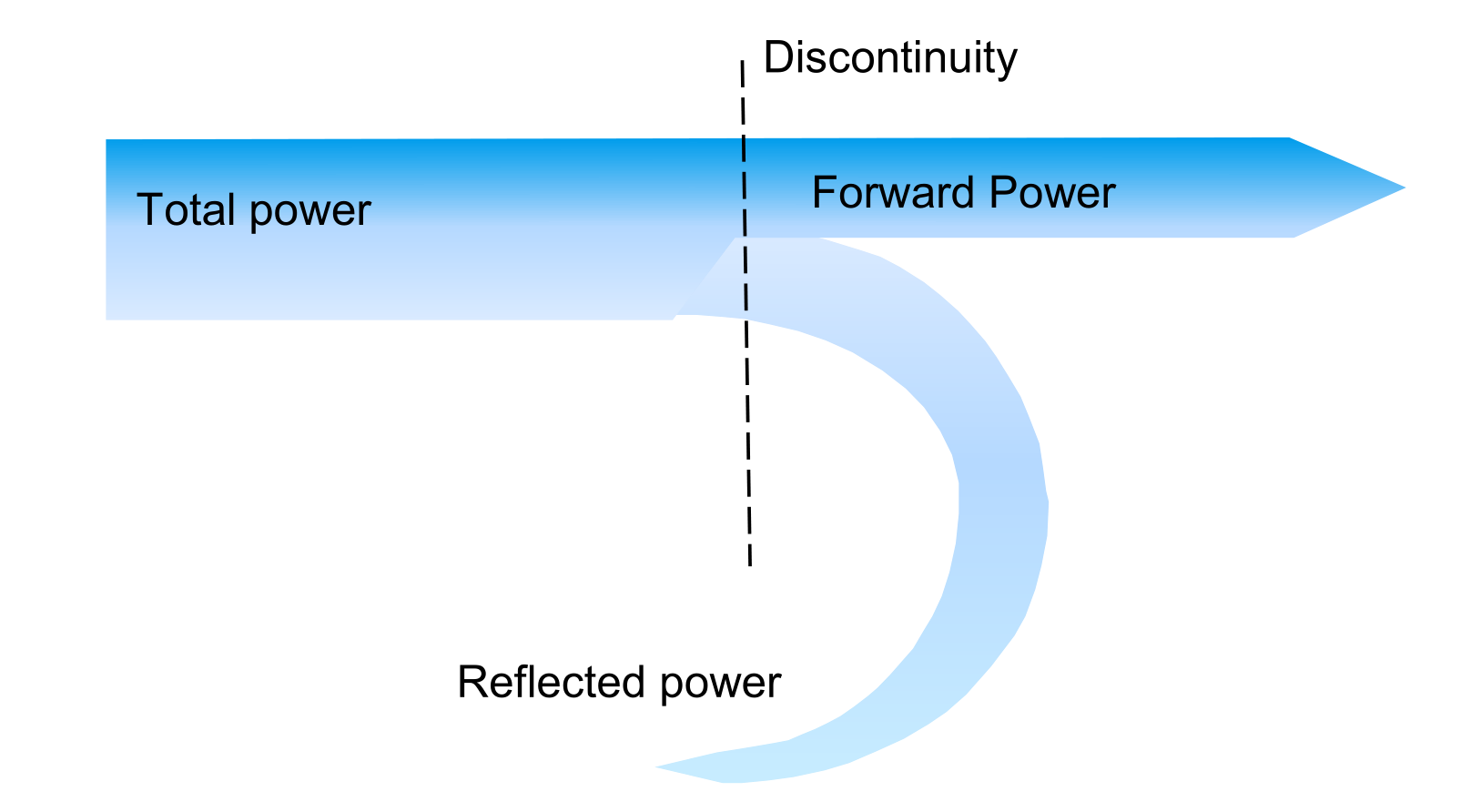
La coincidencia de impedancia se puede observar a través del circuito equivalente de la antena de transmisión, solo cuando se cumple $Z_S=Z_{in}$, se puede lograr la máxima potencia de transmisión:
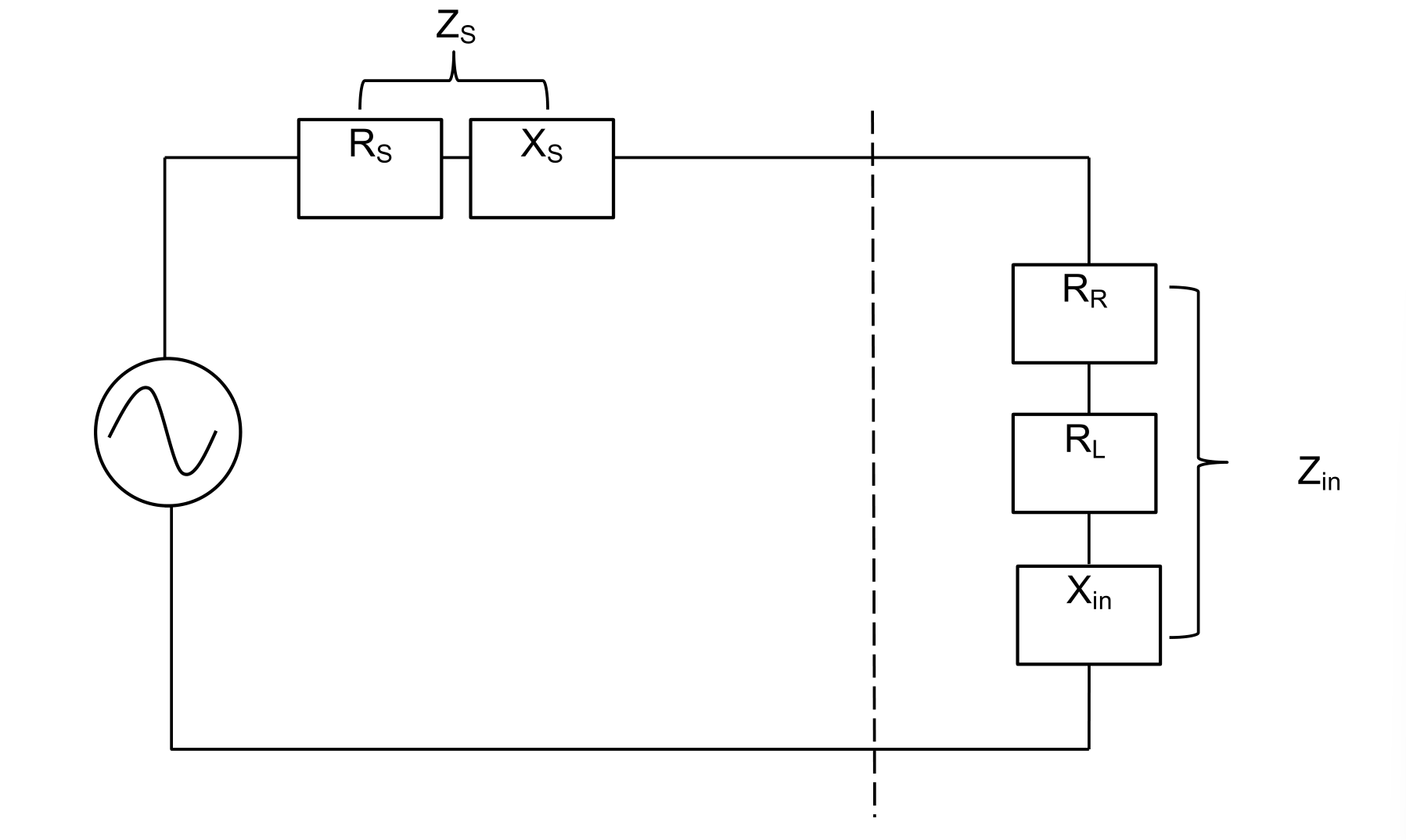
### Relación de Onda Estacionaria de Voltaje (Voltage Standing Wave Ratio, VSWR)
Si no hay coincidencia de impedancia, es posible que algo de energía se refleje, lo que resulta en la generación de ondas estacionarias. Usamos la relación de onda estacionaria $s$ para describir las características de las ondas estacionarias, que se define como la relación entre los valores máximos y mínimos de voltaje en la línea de transmisión (también se puede calcular a partir de la relación de corriente):
$$
s=\frac{V_{max}}{V_{min}}=\frac{I_{max}}{I_{min}}
$$
Además, también se puede calcular la relación de onda estacionaria a partir de las amplitudes (o potencia) de voltaje de entrada $V_{forw}$ y voltaje de reflexión $V_{refl}$:
$$
s=\frac{|V_{forw}|+|V_{refl}|}{|V_{forw}|-|V_{refl}|}=\frac{\sqrt{P_{forw}}+\sqrt{P_{forw}}}{\sqrt{P_{forw}}-\sqrt{P_{forw}}}
$$
La relación de voltaje de reflexión $V_{refl}$ con respecto al voltaje de entrada $V_{forw}$ se llama coeficiente de reflexión $r$ (Reflection Roefficient):
$$
r=\frac{V_{refl}}{V_{forw}
$$
Por lo tanto, la relación de onda estacionaria se puede calcular a partir del coeficiente de reflexión:
$$
r=\frac{1+|r|}{1-|r|}
$$
Además, definimos la forma logarítmica del coeficiente de reflexión como la pérdida de retorno $a_r$ (Return Loss):
$$
a_r=-20log|r|
$$
$$
=-20log\frac{V_{refl}}{V_{forw}}=-10log\frac{P_{refl}}{P_{forw}}
$$
Existen muchos parámetros para medir la calidad de la coincidencia de impedancia, y su relación se muestra de manera sencilla a continuación:
| VSWR | R | \(a_r\) | Energía Reflejada |
|---|---|---|---|
| 1.002 | 0.001 | 60 dB | \ |
| 1.01 | 0.005 | 46 dB | \ |
| 1.1 | 0.05 | 26 dB | 0.2% |
| 1.2 | 0.1 | 20 dB | 0.8% |
| 1.5 | 0.2 | 14 dB | 4% |
| 2.0 | 0.33 | 9.5 dB | 11.1% |
| 2.0 | 0.5 | 6 dB | 25% |
| 5.0 | 0.67 | 3.5 dB | 44.4% |
Factor de Antena
El factor de antena (también conocido como coeficiente de antena o factor de conversión) se utiliza comúnmente en antenas receptoras. Se define como la relación entre la intensidad del campo eléctrico y la tensión de salida medida en el punto de alimentación (a 50Ω):
En la mayoría de los casos, se expresa en forma logarítmica (dBm):
Si la antena ha sido calibrada en fábrica, el valor del factor de antena generalmente es fijo. La relación entre el factor de antena y la ganancia real de la antena se expresa como:
Ancho de Banda
El parámetro de ancho de banda de una antena se utiliza para medir el rango de frecuencia en el cual la antena puede operar satisfactoriamente. Los estándares de ancho de banda generalmente se basan en la coincidencia de impedancia (VSWR<1.5), aunque el rendimiento de la antena, la ganancia y otros parámetros también pueden utilizarse como criterios de ancho de banda.
Para antenas de banda ancha (Broadband Antennas), la relación entre la frecuencia más alta y la más baja es fija. Por ejemplo, una relación de 2:1 se llama doble banda y una relación de 10:1 se llama diez veces la banda:
El término de banda ancha se refiere a BW≥2. Además, hay otra definición de ancho de banda que se aplica solo a antenas de banda estrecha (Narrowband Antennas):
Donde \(f_C\) es la frecuencia central. El valor de este ancho de banda puede superar el 100% (≤200%).
Referencias y Agradecimientos
- 《Antenna-Basics_Rohde&Schwarz》
- 《如何選擇天線於微波系統_Rohde&Schwarz》
- 天线增益 | WLAN 天线快速入门
- What Is Antenna Gain
Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.