Fundamentos del Diagrama de Smith y Circuitos de Coincidencia
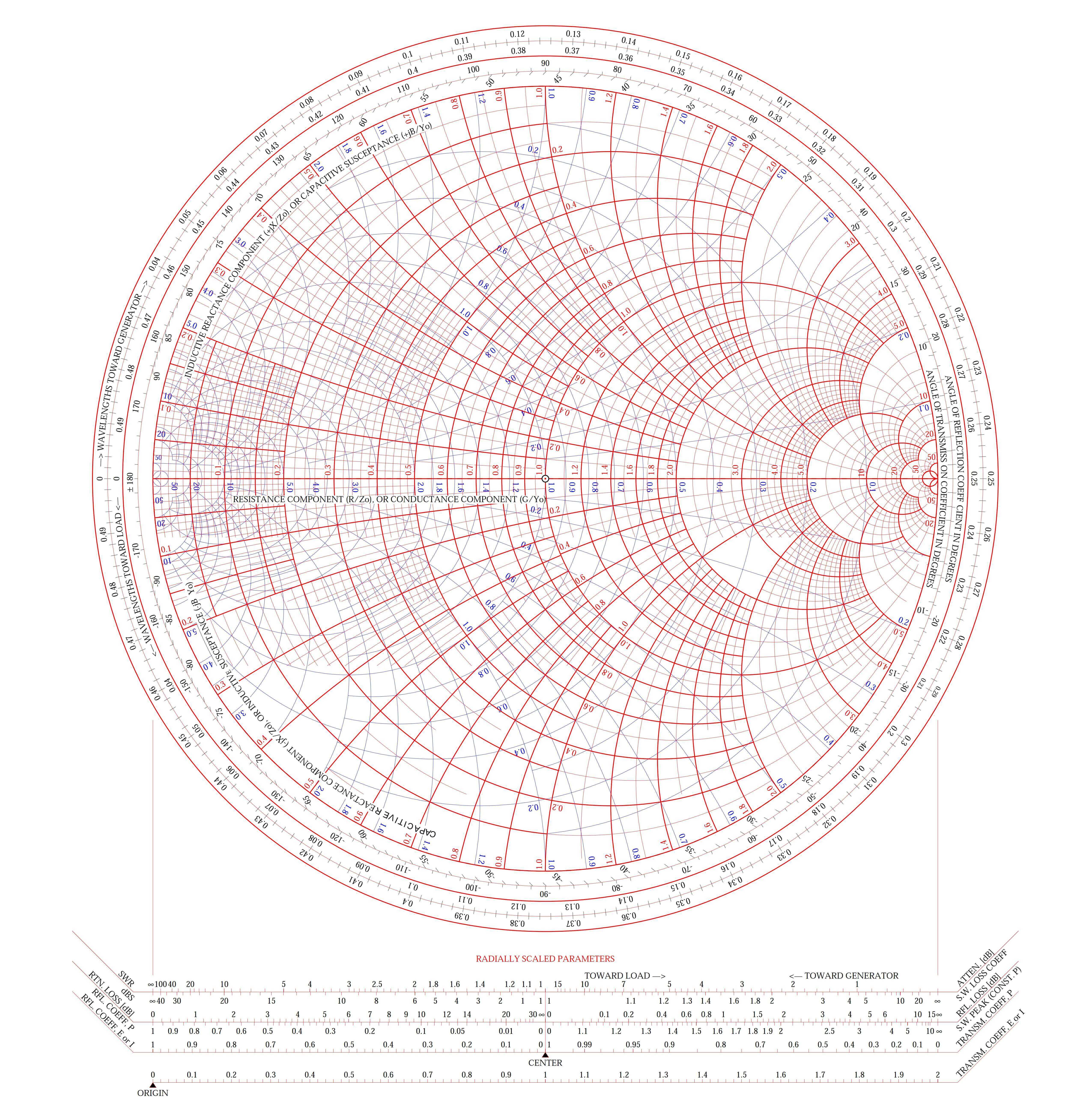
El Diagrama de Smith es un gráfico de coordenadas polares que representa el coeficiente de reflexión complejo (Γ gamma). Este gráfico representa simultáneamente la parte real e imaginaria de la impedancia compleja. En este gráfico, la parte real R varía desde 0 hasta el infinito (∞), y la parte imaginaria X varía desde menos infinito hasta más infinito, lo que permite representar ambos en el mismo gráfico. El Diagrama de Smith puede utilizarse para representar parámetros y funciones que incluyen, entre otros:
- Impedancia compleja
- Coeficiente de reflexión complejo
- Relación de onda estacionaria de voltaje (VSWR)
- Efectos de líneas de transmisión
- Diseño de redes de coincidencia de impedancia
Impedancia Normalizada
El primer paso es normalizar la impedancia compleja antes de representarla en el Diagrama de Smith. La impedancia normalizada es igual a la impedancia real dividida por la impedancia del sistema:
En la mayoría de los casos, la impedancia del sistema es de 50Ω, por lo que, en general, se divide la impedancia real entre 50Ω. Por ejemplo, si la impedancia real es (37+j55)Ω, la impedancia normalizada es aproximadamente (0.74+j1.10)Ω.
Detalles del Diagrama de Smith
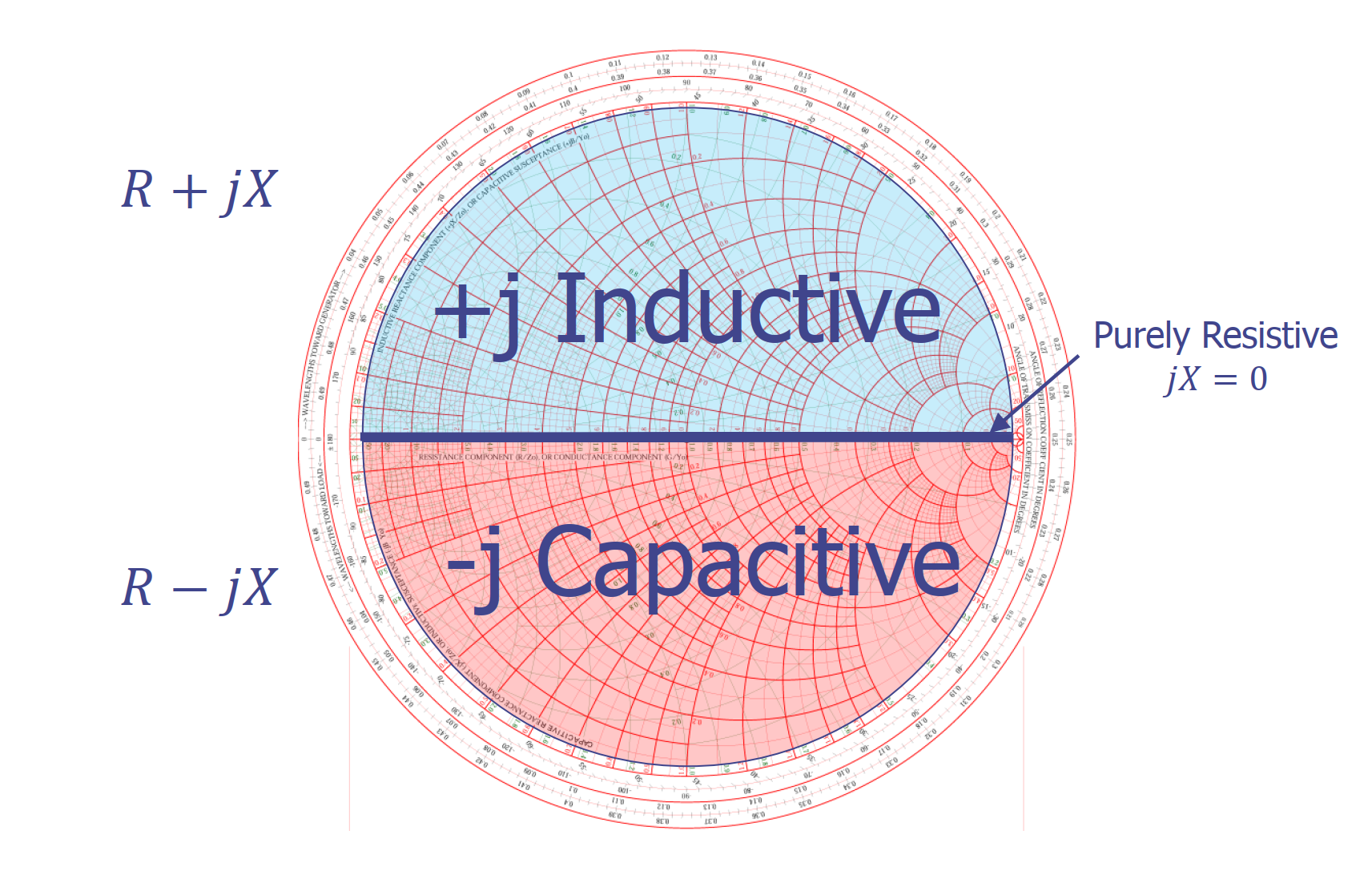
En el Diagrama de Smith, el eje horizontal central representa la resistencia pura (R). En este eje, la reactancia es siempre igual a 0. En la región por encima del eje principal (R+jX), la reactancia es inductiva, mientras que en la región por debajo del eje principal (R-jX), la reactancia es capacitiva.
Puntos Clave
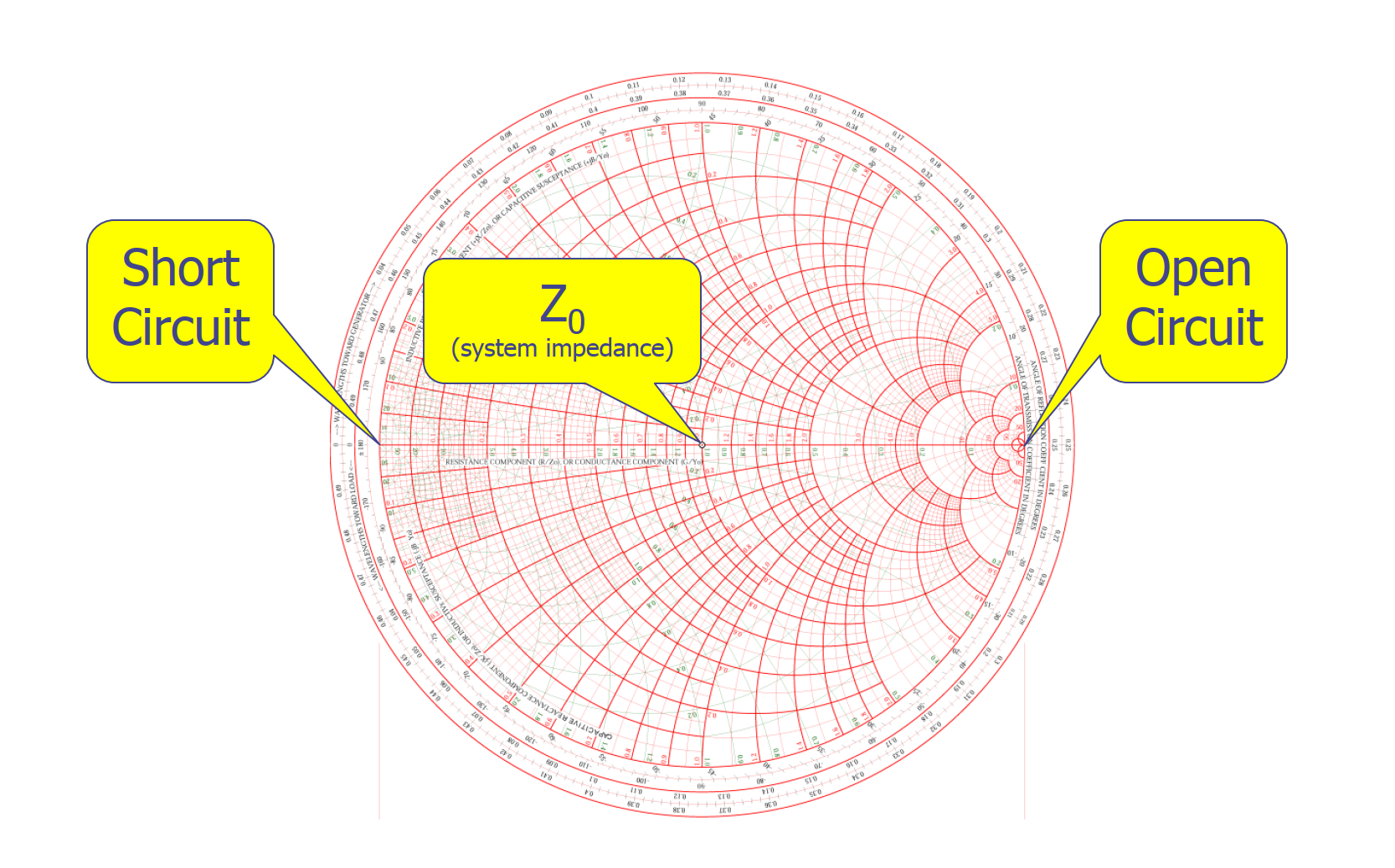
En el Diagrama de Smith, hay varios puntos clave. El punto central representa la impedancia del sistema (en un sistema de 50Ω, el punto central representa 50Ω). Siguiendo el eje principal, el punto más a la derecha representa un circuito abierto (impedancia infinita), mientras que el punto más a la izquierda representa un cortocircuito (impedancia igual a 0).
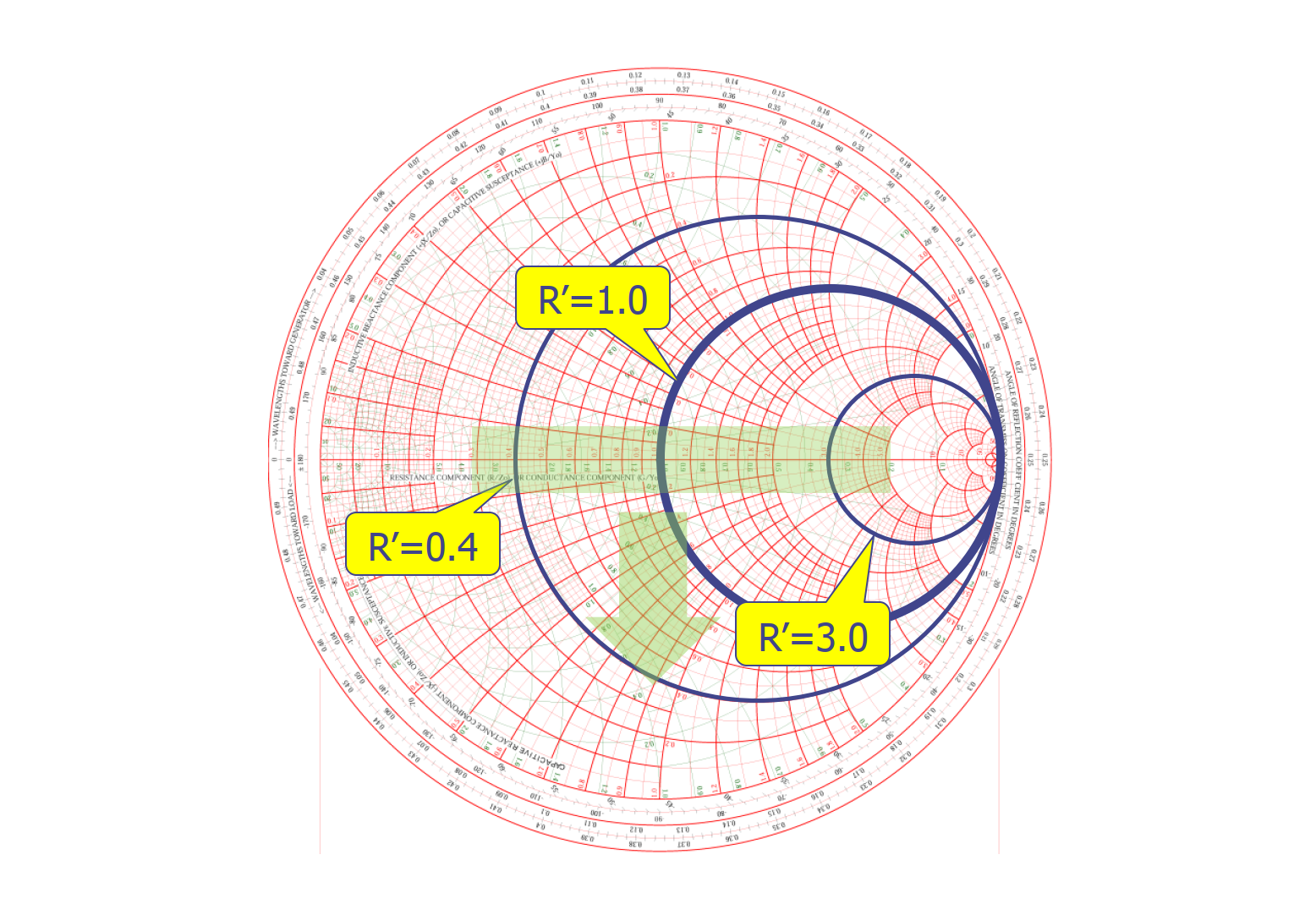
Círculos de Resistencia Constante
En los círculos de resistencia constante, la parte normalizada de la resistencia (parte real) es constante. Por ejemplo, el círculo que pasa a través del punto central tiene una resistencia de 1 (50Ω), lo que significa que la parte normalizada de la impedancia es 1. En el gráfico, también se pueden ver círculos con una parte normalizada de resistencia de 0.4 y 3.0.
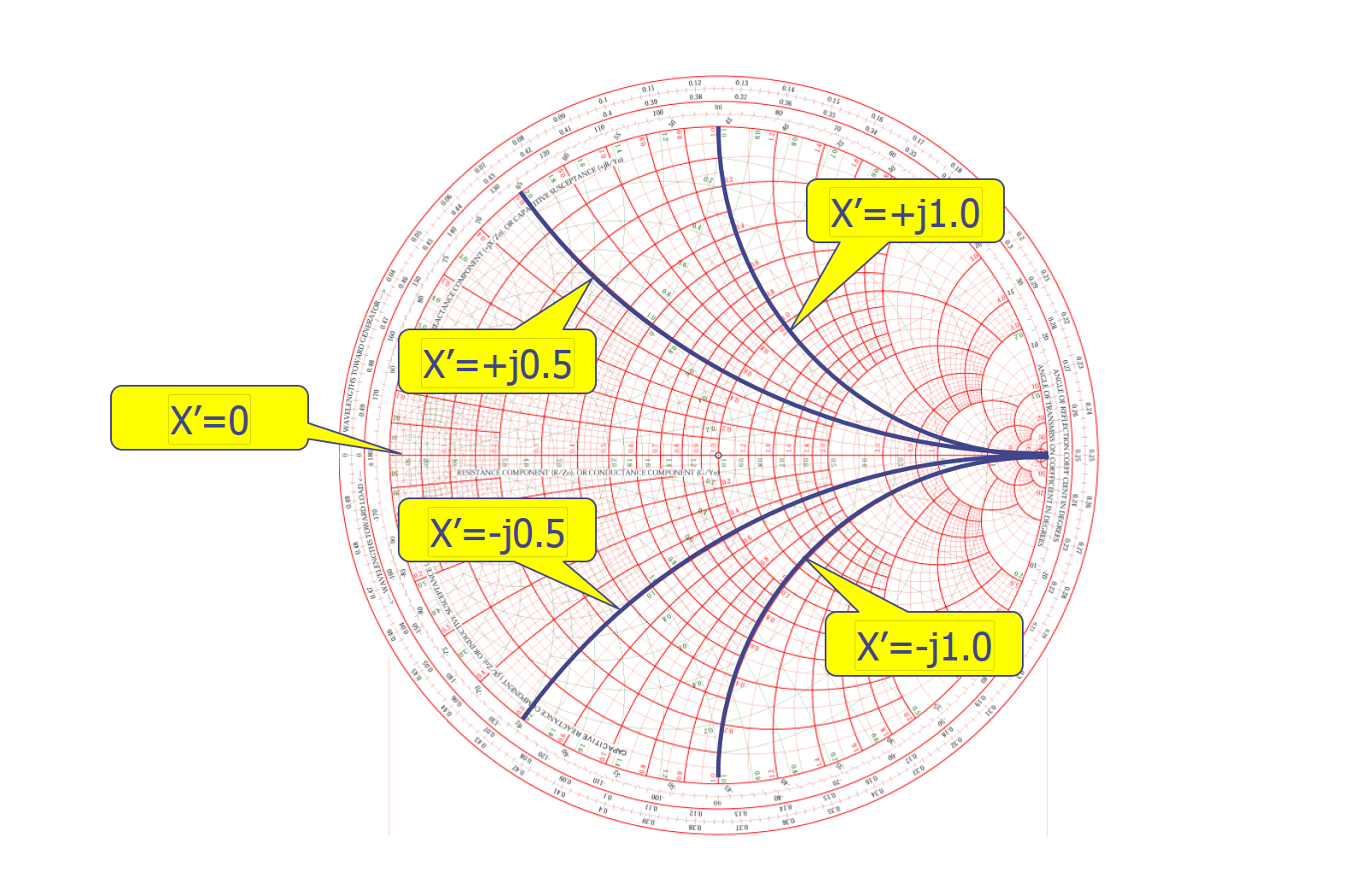
Arcos de Reactancia Constante
Los arcos de reactancia constante se extienden desde el punto de circuito abierto y representan el valor de la reactancia, es decir, la parte imaginaria de la impedancia compleja. A medida que el ángulo del arco aumenta, el valor absoluto de la reactancia aumenta. A medida que el ángulo del arco disminuye, el valor absoluto de la reactancia disminuye, hasta llegar a 0 (cuando se encuentra en el eje de resistencia pura y no muestra inductancia o capacitancia). En el gráfico, se pueden ver arcos de reactancia constante con valores de reactancia de ±0.5 (imaginaria ±j0.5) y ±1.0 (imaginaria ±j1.0).
Conversión de Impedancia Compleja a Admitancia Compleja
La admitancia (Y) es el recíproco de la impedancia, la conductancia (G) es el recíproco de la resistencia, y la susceptancia (B) es el recíproco de la reactancia. Cuando estos valores son complejos, los cálculos pueden ser complicados. Sin embargo, en el Diagrama de Smith, basta con trazar un círculo con centro en el punto de impedancia compleja Z' para encontrar el valor correspondiente de la admitancia compleja Y'.
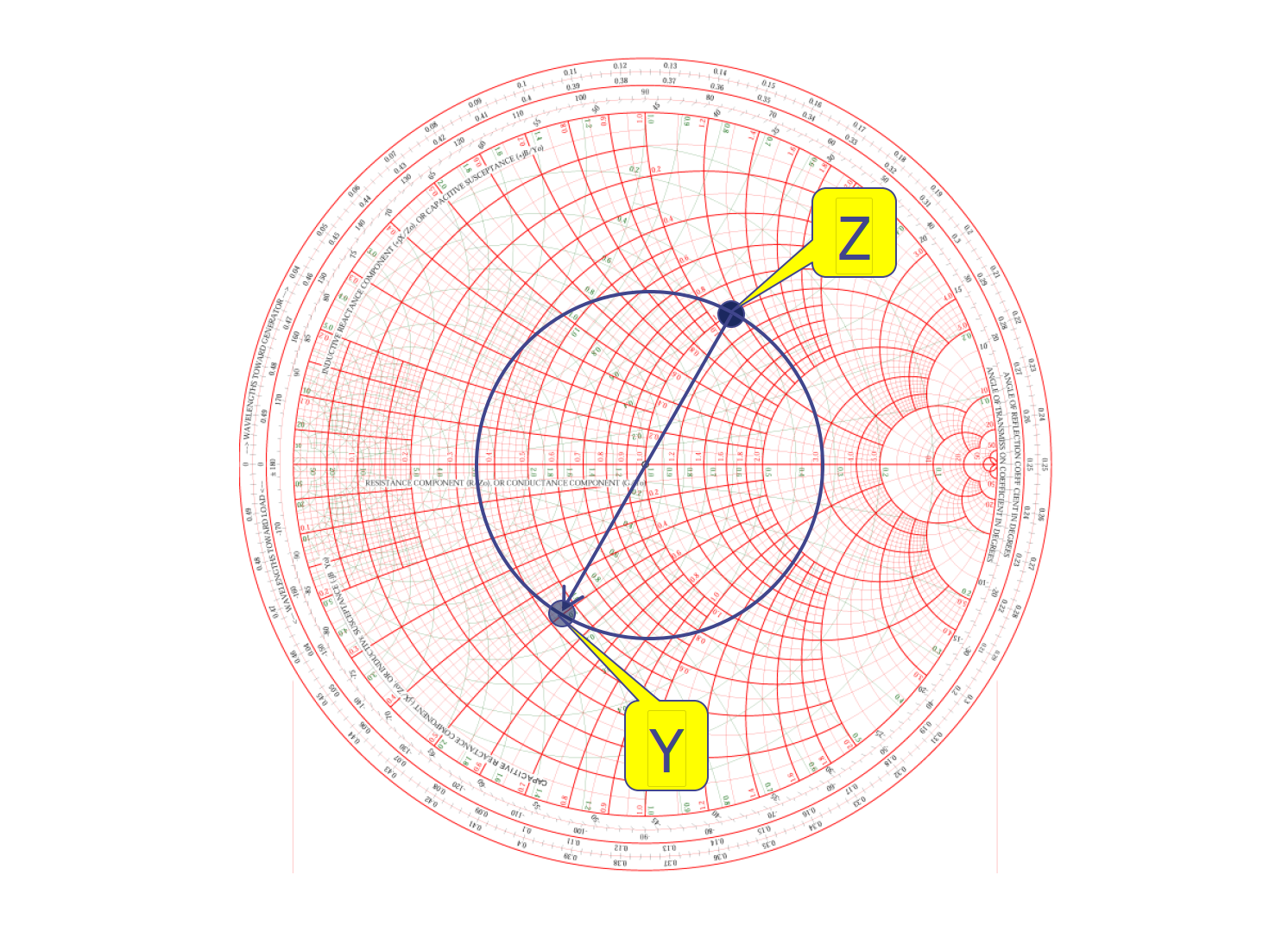
Por ejemplo, si Z'=1+j1.1, entonces Y'=0.45-j0.5.
Si se trata de una curva de impedancia compleja, se puede girar el Diagrama de Smith 180° para obtener la curva correspondiente de admitancia compleja.
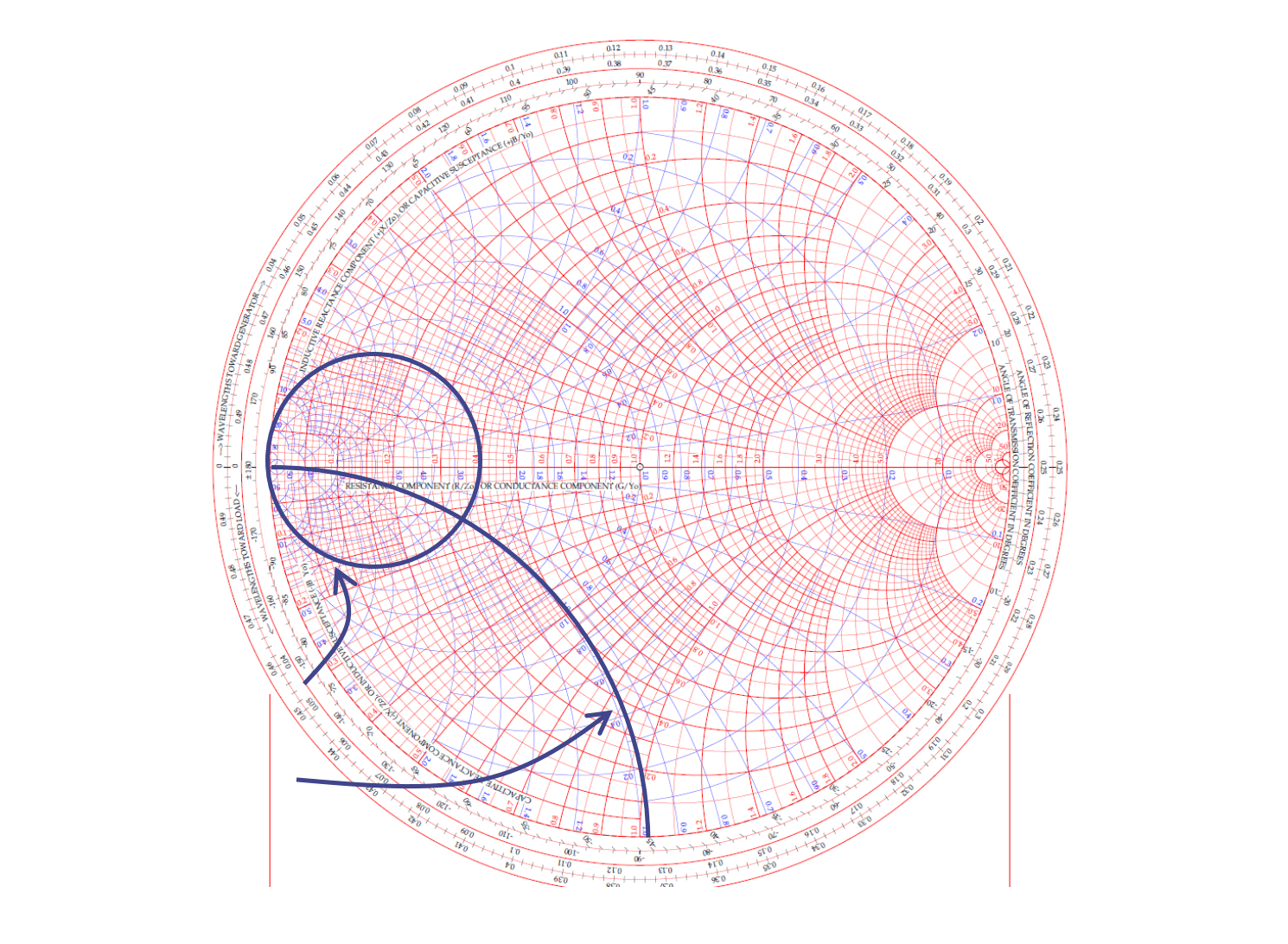
Círculos de Admitancia Constante y Arcos de Susceptancia Constante
En el Diagrama de Smith completo, también se presentan los círculos de admitancia constante y los arcos de susceptancia constante, marcados en azul en la siguiente imagen:
Marcando Valores Generales en el Diagrama de Smith
Para marcar valores generales en el Diagrama de Smith, como Z=25+j40, primero debemos normalizarlo en relación con la impedancia de 50Ω. Calculamos Z'=0.5+j0.8. Luego, podemos buscar en el gráfico el círculo con una parte normalizada de resistencia R'=0.5 y un arco con una parte normalizada de reactancia X'=0.8, y el punto de intersección será el valor buscado Z'.
### Parámetros de Escala Radial del Gráfico de Smith
Por lo general, debajo del gráfico de Smith hay un eje de parámetros de escala radial. Supongamos que hay un punto de impedancia compleja en el gráfico, conéctelo al punto central y gire a lo largo del radio hacia el eje principal, proyectándolo en el eje de parámetros de escala radial, como se muestra en la imagen:

En este eje, se pueden leer varios parámetros:
- Relación de onda estacionaria de voltaje (VSWR): 2.3:1
- Pérdida de retorno (Return Loss): 8.10 dB
- Coeficiente de reflexión (Reflection Coefficient)
- Voltaje: 0.155
- Potencia: 0.39
Además, podemos observar que los puntos en este círculo de radio tienen estos mismos parámetros.
### Relación entre la Relación de Onda Estacionaria y la Línea de Transmisión
Como se mencionó anteriormente, en un círculo dibujado con el punto de impedancia del sistema (punto central) como centro y la distancia al punto de impedancia compleja como radio, los puntos en el círculo con diferentes impedancias tienen la misma Relación de Onda Estacionaria (SWR). El recorrido completo alrededor del círculo equivale a una longitud de onda / 2. Por lo tanto, **cada vez que la longitud de la línea de transmisión aumenta en un múltiplo de media longitud de onda, la impedancia compleja dará una vuelta completa en el círculo**.
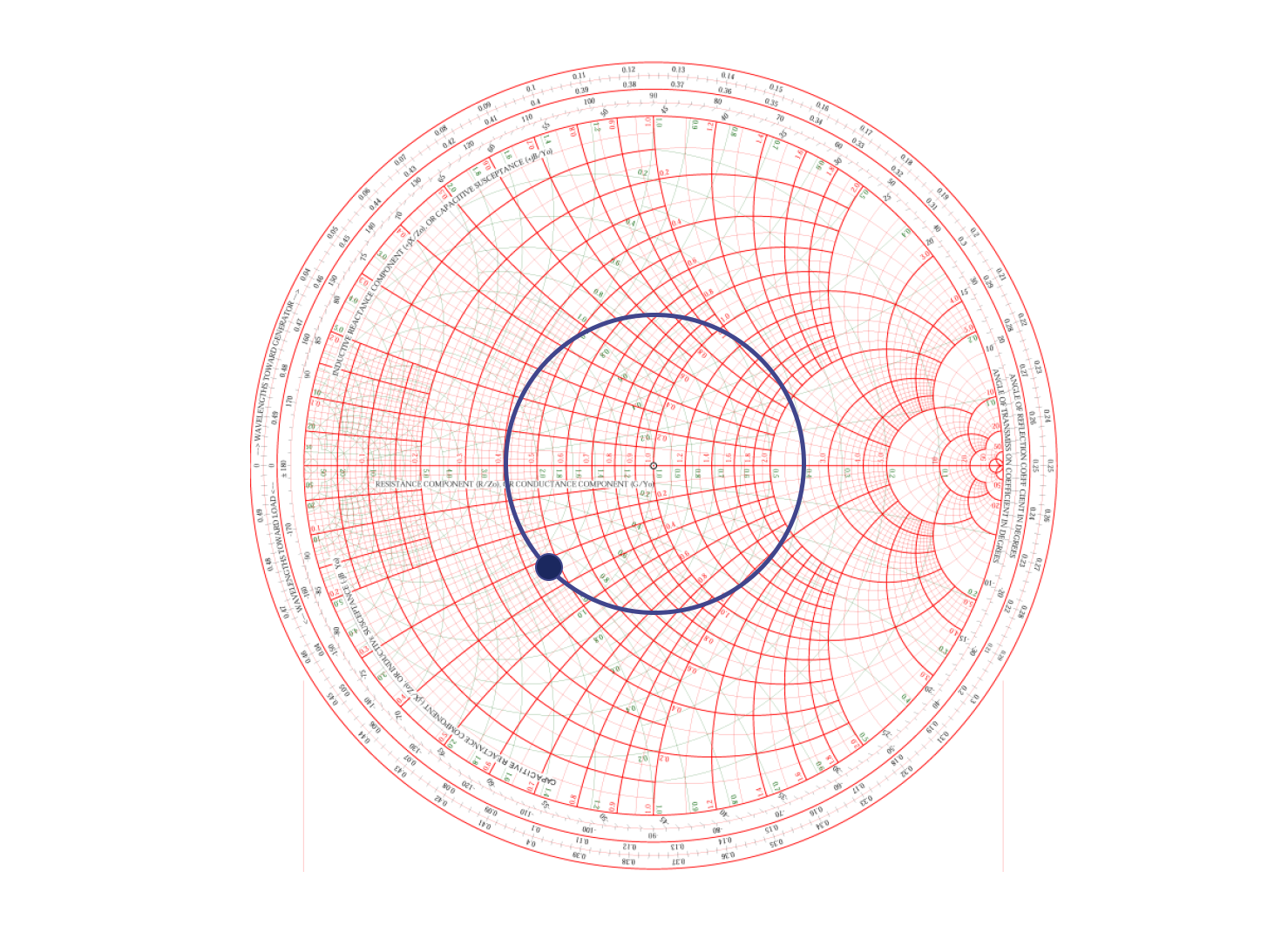
Por lo tanto, la longitud de la línea de transmisión desde la fuente hasta la antena debe controlarse para que sea un múltiplo entero de la mitad de la longitud de onda de la antena. Esto evita que la impedancia medida se desvíe de la impedancia real de la antena. Si la longitud no es un valor estándar, se puede utilizar el modelo de línea de transmisión en el software de simulación [**SimNEC**](http://www.ae6ty.com/smith_charts.html) para realizar ajustes.
Otro fenómeno interesante es que si la longitud de la línea de transmisión termina en un circuito abierto y es igual a un cuarto de longitud de onda (media vuelta), parece un cortocircuito; y si la longitud de la línea de transmisión con un circuito cerrado es igual a un cuarto de longitud de onda, la característica aparente es como un circuito abierto:
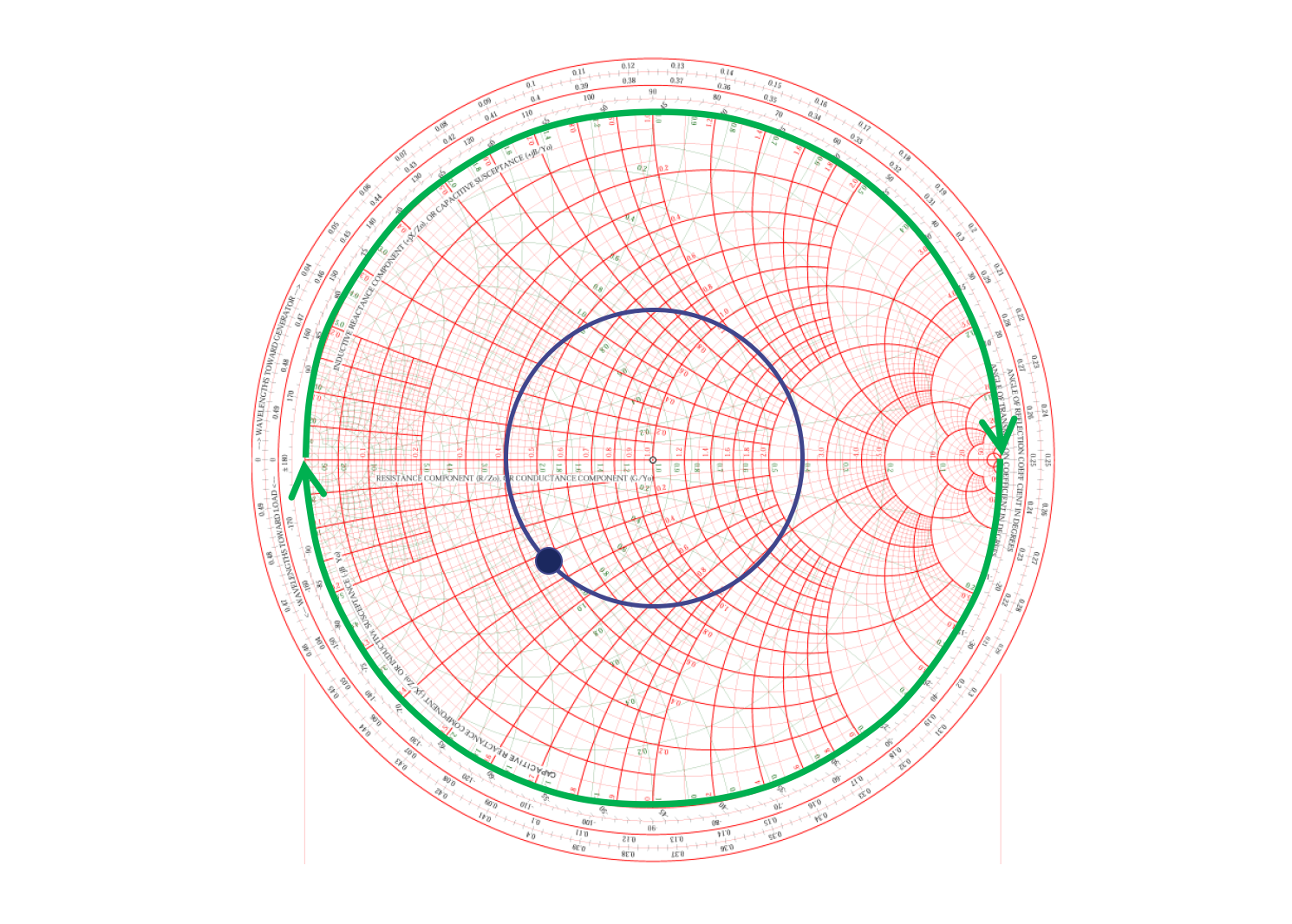
## Diseño de Circuitos de Coincidencia
Normalmente, en un circuito, conectamos inductores y capacitores en serie o paralelo para ajustar la impedancia al valor deseado.
- **Inductor en serie**: se mueve en sentido horario a lo largo del círculo de resistencia constante.
- **Capacitor en serie**: se mueve en sentido antihorario a lo largo del círculo de resistencia constante.
- **Inductor en paralelo**: se mueve en sentido antihorario a lo largo del círculo de conductancia constante.
- **Capacitor en paralelo**: se mueve en sentido horario a lo largo del círculo de conductancia constante.
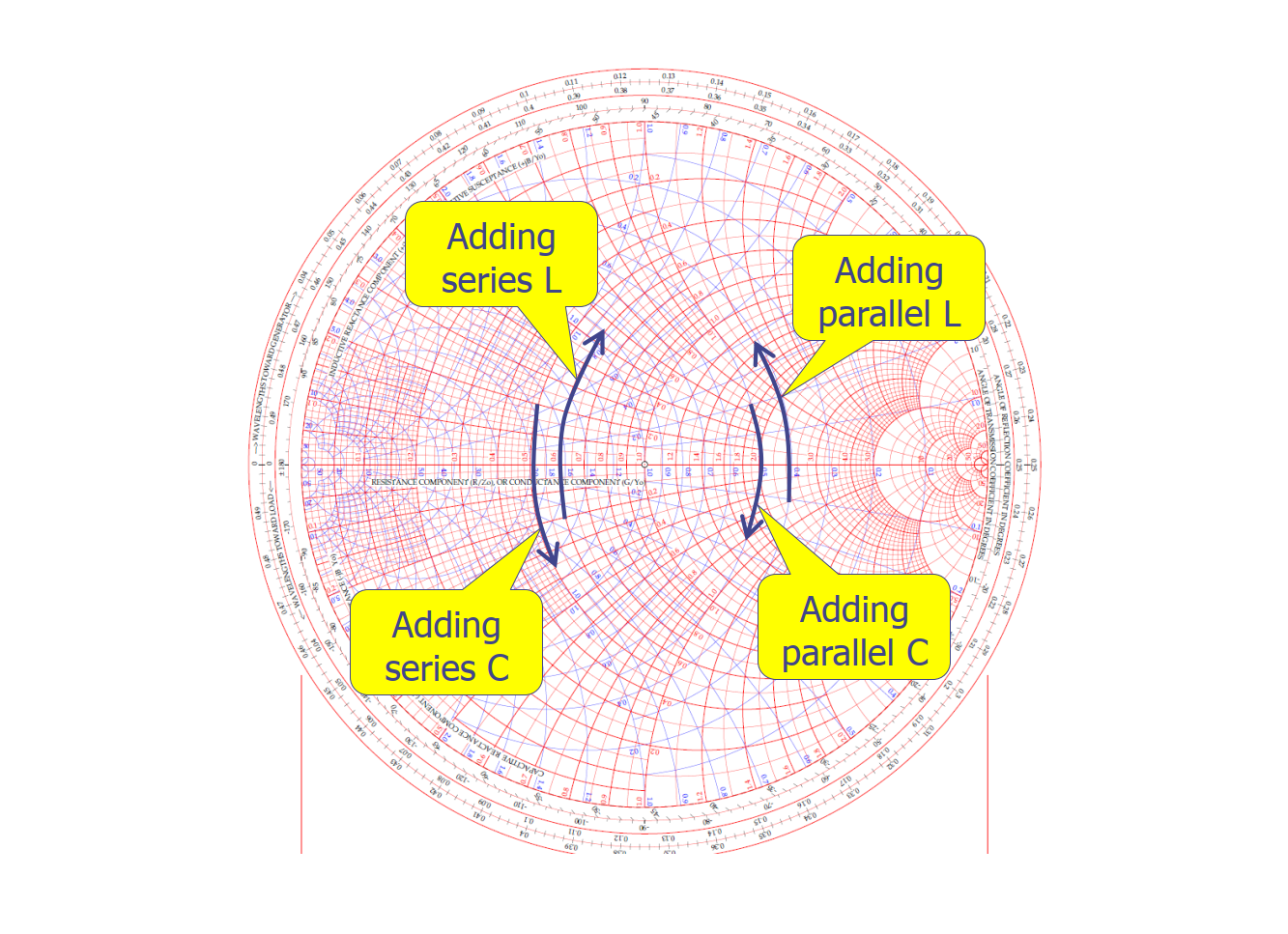
En términos cualitativos, tanto si se conecta en serie como en paralelo, agregar un inductor hará que el punto de impedancia compleja suba, mientras que agregar un capacitor hará que baje.
## Circuito de Coincidencia en Forma de L Simple
Supongamos que la impedancia compleja medida en el circuito actual es $Z_L$, y necesitamos ajustarla a la impedancia deseada $Z_0$ (preferiblemente en el punto central, o en el círculo de resistencia de 50Ω). Podemos utilizar inductores o capacitores para construir un circuito de coincidencia simple en forma de L y mover el punto de impedancia compleja en el gráfico de Smith. La combinación de inductores o capacitores dependerá de la posición inicial de $Z_L$ en el gráfico de Smith. Puede elegir la combinación adecuada para construir el circuito de coincidencia en forma de L según la distribución de $Z_L$ en el gráfico de Smith, como se muestra en la siguiente imagen:
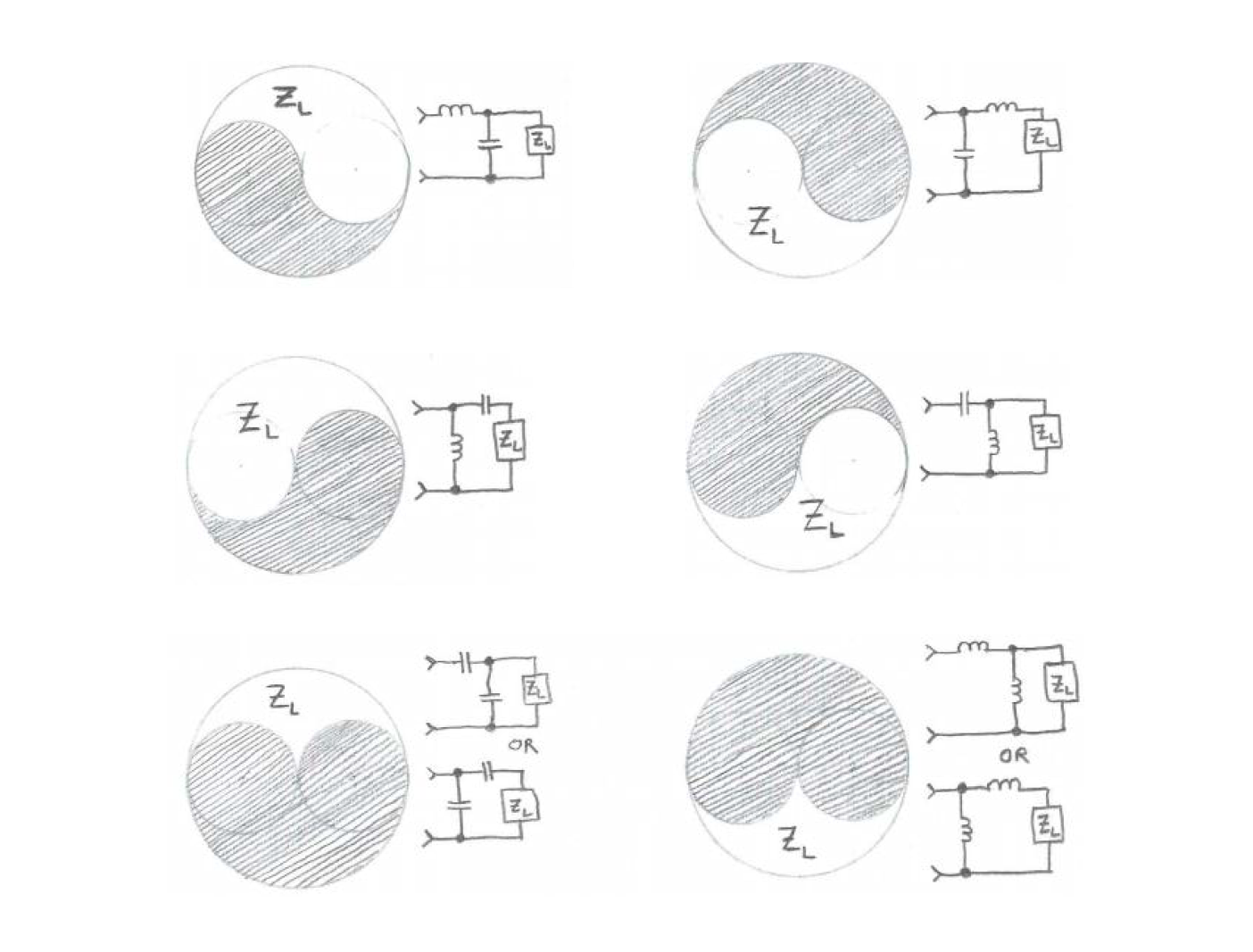
Por ejemplo, si la impedancia compleja inicial $Z_L$ es como se muestra en la siguiente imagen (punto negro), podemos construir el circuito de coincidencia en forma de L según el diseño en la imagen más pequeña para llevarlo a la impedancia deseada $Z_0$ (punto rojo):
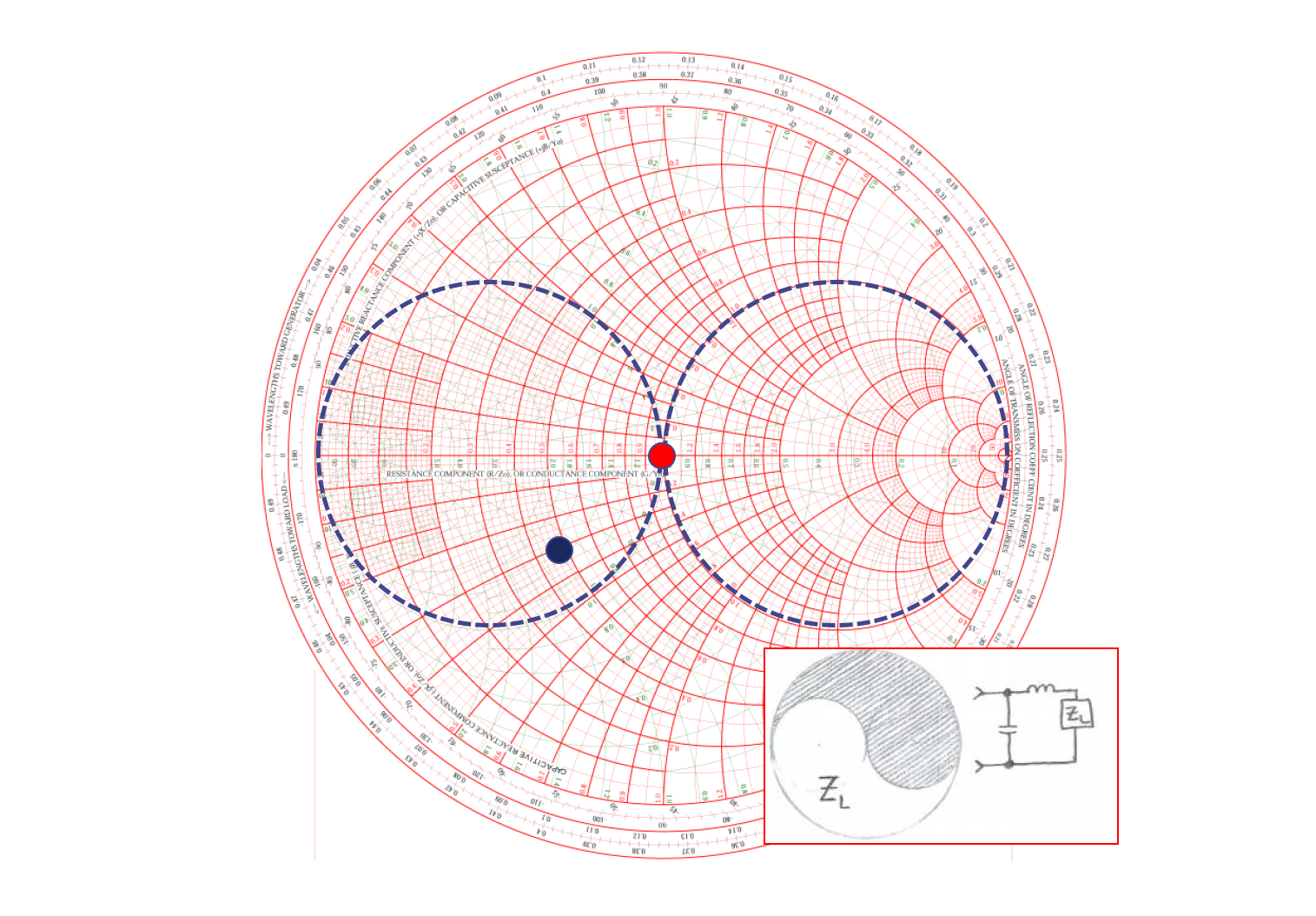
Para facilitar el ajuste, hemos trazado los círculos de conductancia constante y resistencia constante en la imagen. Los pasos posteriores se pueden realizar en el software de simulación [**SimNEC**](http://www.ae6ty.com/smith_charts.html):
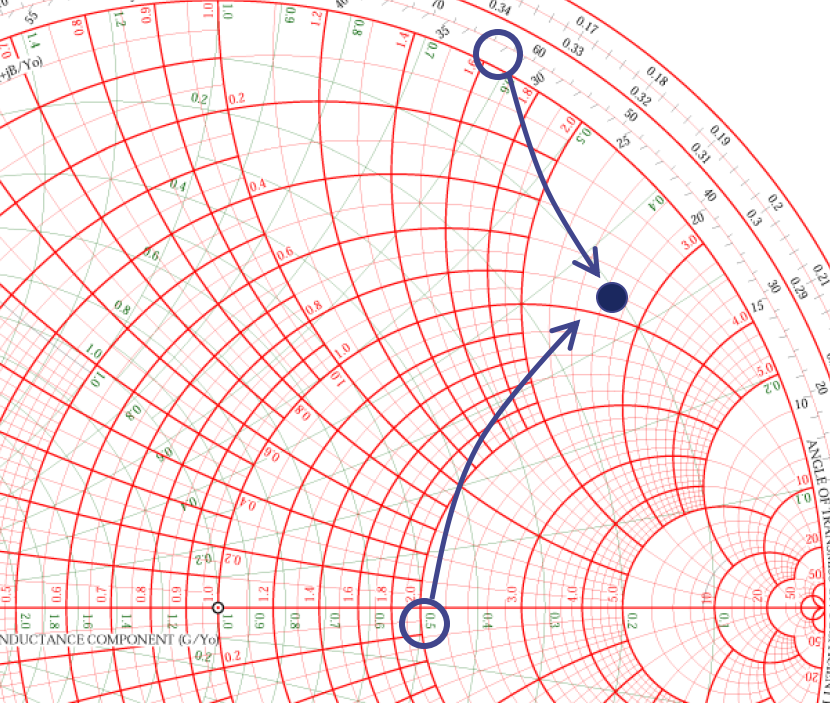
1. Agregue un inductor en serie, gire en sentido horario a lo largo del círculo de resistencia constante hasta que toque el círculo de conductancia constante.
2. Agregue un capacitor en paralelo, gire en sentido horario a lo largo del círculo de conductancia constante hasta llegar al punto central.
Por favor, hágame saber si necesita alguna aclaración o modificación adicional.
El método puede resumirse aproximadamente de la siguiente manera: comenzando desde el punto cercano a la carga, se agrega el primer componente para desplazar el punto de impedancia hacia el círculo de admitancias constante o el círculo de impedancias constante estándar; luego se agrega un segundo componente para moverlo hacia el punto central a lo largo del círculo de admitancias constante o el círculo de impedancias constante estándar. Los valores de los componentes seleccionados se pueden leer en el software.
Para obtener información detallada sobre la configuración de circuitos de antena en la práctica, puede consultar el artículo Diseño de Circuitos de Emparejamiento de Antenas en General.
Referencias y Agradecimientos
- El Gráfico de Smith: Su Historia y Por Qué Es Tan Importante para los Diseñadores de RF
- Conceptos Básicos del Gráfico de Smith - Introducción, Impedancia, VSWR, Líneas de Transmisión, Emparejamiento
- Conceptos Básicos de Ingeniería de RF: el Gráfico de Smith
Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.