Integridad de la Señal - Impedancia y Modelos Eléctricos
La impedancia (Electrical Impedance, Z) se refiere colectivamente a la resistencia, la inductancia y la capacitancia en un circuito, y describe cómo afectan a las corrientes alternas. Se define como la relación entre el voltaje y la corriente (\(Z=V/I\)). La impedancia es un número complejo, donde la parte real es la resistencia y la parte imaginaria es la reactancia. La capacitancia en un circuito se refiere a la reactancia capacitiva, y la inductancia se refiere a la reactancia inductiva. La combinación de capacitancia e inductancia se conoce como impedancia.
Cuanto mayor sea la impedancia, menor será la corriente que fluye para un voltaje constante, y viceversa. En situaciones extremas, la impedancia en un circuito abierto es infinita, mientras que en un cortocircuito es cero. En el caso de las líneas de interconexión, la impedancia es un factor crítico que afecta a las señales. Durante la propagación de una señal, esta responde en función de la impedancia instantánea.
Modelo Eléctrico Básico
Al crear un modelo eléctrico básico, consideramos varios componentes ideales de dos terminales:
- Resistor ideal.
- Condensador ideal.
- Inductor ideal.
- Línea de transmisión ideal.
La combinación de resistencia, capacitancia y reactancia se denomina elemento del circuito total. Por otro lado, las características de una línea de transmisión ideal se distribuyen a lo largo de la línea. El objetivo es construir un modelo de circuito equivalente que se acerque lo más posible a las mediciones reales de impedancia de los componentes.

Impedancia de un Resistor Ideal en el Dominio del Tiempo
La impedancia de un resistor ideal es constante y su valor es igual a la resistencia. No depende del voltaje ni de la corriente.
Impedancia de un Condensador Ideal en el Dominio del Tiempo
Para un condensador ideal, la carga almacenada entre sus placas está relacionada con la diferencia de voltaje de la siguiente manera:
Donde C representa la capacitancia (unidad: Faradios), Q es la carga almacenada entre las placas (unidad: Coulombs), y V es la diferencia de voltaje entre las placas (unidad: Voltios).
La impedancia del condensador se calcula a partir de la relación entre el voltaje en sus terminales y la corriente que fluye a través de él. En realidad, no fluye corriente a través del condensador, sino que parece haber corriente cuando el voltaje entre las placas del condensador cambia.
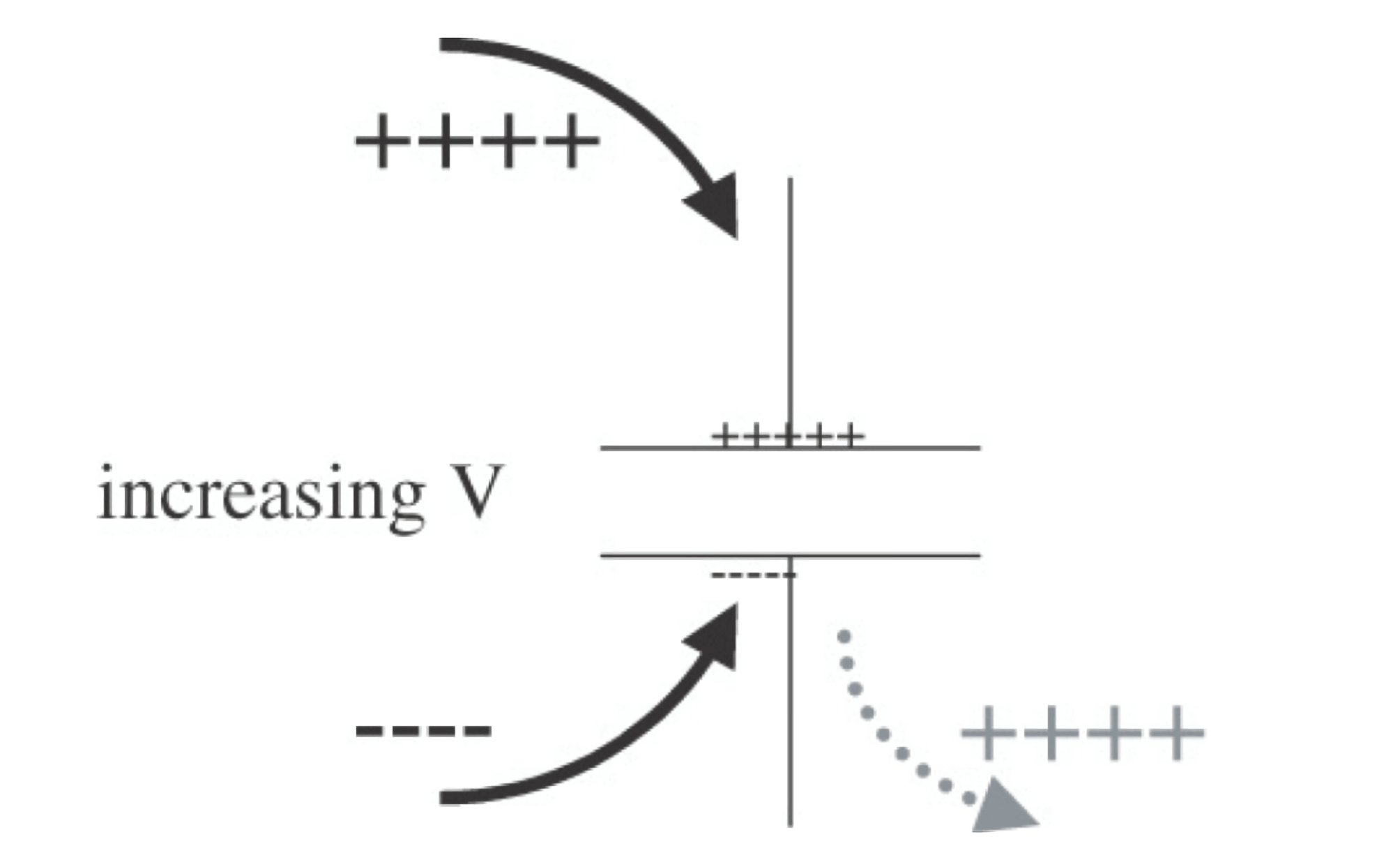
Como se muestra en la imagen, cuando la placa superior acumula una carga positiva y la placa inferior acumula una carga negativa, esto parece indicar que hay una corriente a través del condensador. Esta corriente, generada por el desplazamiento de las cargas ligadas en un dieléctrico polarizado, se llama corriente de desplazamiento. No es una corriente real, sino simplemente el movimiento de cargas. Se define como:
Como se desprende de la ecuación, solo hay corriente cuando el voltaje en los terminales del condensador cambia. Si el voltaje se mantiene constante, no hay corriente de desplazamiento.
Por lo tanto, la impedancia del condensador ideal se expresa como:
La impedancia del condensador depende de la forma de onda del voltaje en sus terminales. Si el voltaje cambia rápidamente (alta pendiente de la onda), la corriente es alta y la impedancia es baja; de manera similar, para un cambio de voltaje más lento, una mayor capacitancia resulta en una impedancia más baja.
Impedancia de un Inductor Ideal en el Dominio del Tiempo
Para un inductor ideal, la diferencia de voltaje en sus terminales se define como:
Donde V representa la diferencia de voltaje a través del inductor, L es el valor del inductor e I es la corriente que fluye a través del inductor. La diferencia de voltaje a través del inductor depende de la velocidad de cambio de la corriente que fluye a través de él, que, a su vez, depende de la diferencia de voltaje entre los terminales. La dirección de la causalidad entre la diferencia de voltaje entre los terminales y la tasa de cambio de corriente depende de cuál sea la fuente impulsora. La impedancia del inductor se puede expresar como la relación entre la diferencia de voltaje en sus terminales y la corriente que fluye a través de él:
Si la corriente que fluye a través del inductor aumenta rápidamente, la impedancia será alta, y viceversa. Para corriente continua, la impedancia se aproxima a cero. La impedancia real del inductor depende de la forma específica de la onda de corriente.
Impedancia en el Dominio de Frecuencia
Como se observó anteriormente, en el dominio del tiempo, los cálculos de impedancia para inductores y condensadores son funciones relativamente complejas. Sin embargo, en el dominio de la frecuencia, el análisis es mucho más simple.
El análisis en el dominio de la frecuencia se realiza considerando que solo existen ondas sinusoidales, y se investiga cómo interactúan con los componentes ideales. Las características clave de una onda sinusoidal son su frecuencia, amplitud y fase, que generalmente se describen en radianes. La relación entre la frecuencia angular (\(\omega\)) y la frecuencia (\(f\)) es:
Cuando aplicamos una señal sinusoidal a los terminales de un componente ideal, observamos la corriente resultante. La impedancia sigue siendo la relación entre la onda sinusoidal de voltaje y la on
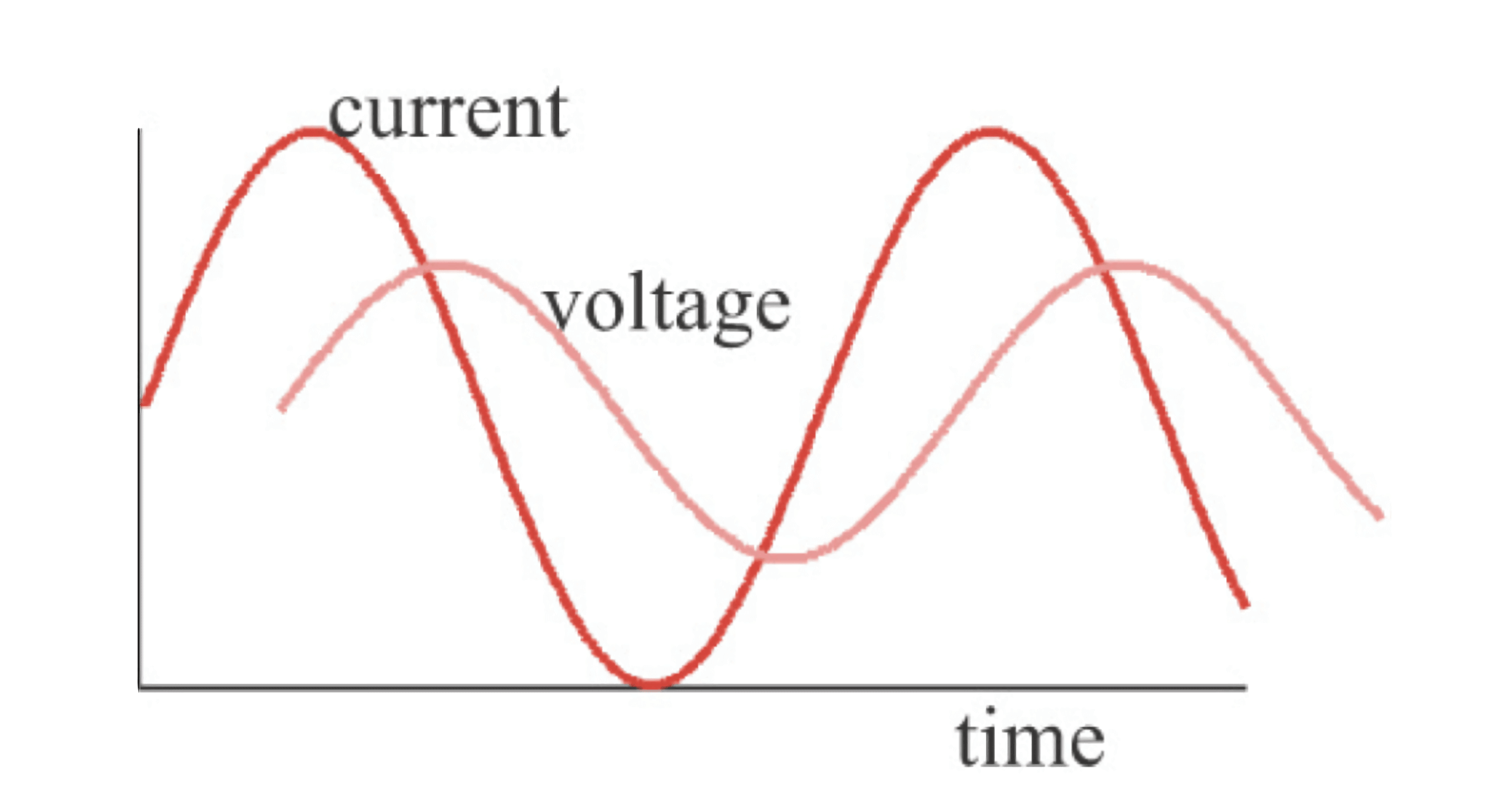
Según la definición de impedancia, la magnitud de la impedancia puede expresarse como:
Al mismo tiempo, es necesario calcular la diferencia de fase entre las dos formas de onda. En el dominio de frecuencia, la impedancia se puede representar de la siguiente manera: a 10 MHz, la magnitud de la impedancia es de 20 Ω, y la fase es de 30° (el voltaje está adelantado 30° con respecto a la corriente). Estos tres elementos son esenciales, ya que tanto la magnitud de la impedancia como la fase dependen de la frecuencia y varían con cambios en la frecuencia. Además, la impedancia en el dominio de frecuencia también se puede representar en forma de números complejos para simplificar los cálculos, incluyendo la información de fase en los números complejos.
Impedancia de un resistor ideal en el dominio de frecuencia
A continuación, analizamos la impedancia de componentes ideales en el dominio de frecuencia. Dado que solo se deben considerar voltajes y corrientes sinusoidales en el dominio de frecuencia, si aplicamos una corriente sinusoidal a un resistor, se generará un voltaje sinusoidal en sus terminales que se puede expresar como:
El voltaje sinusoidal es simplemente el producto de la corriente sinusoidal y la resistencia. De acuerdo con la fórmula anterior, la impedancia de un resistor ideal se puede expresar como:
De hecho, la impedancia de un resistor ideal es igual a su valor de resistencia y no depende de la frecuencia, con una diferencia de fase de cero. Este resultado concuerda con lo que obtendríamos en el dominio del tiempo.
Impedancia de un capacitor ideal en el dominio de frecuencia
Para analizar la impedancia de un capacitor ideal en el dominio de frecuencia, es necesario aplicar un voltaje sinusoidal en sus terminales. La corriente que fluye a través del capacitor se puede expresar como:
Se puede observar que incluso si el voltaje es constante, la corriente varía con la frecuencia, aumentando a medida que la frecuencia aumenta. Esto significa que la impedancia de un capacitor disminuye a medida que la frecuencia aumenta y se puede expresar como:
La magnitud de la impedancia es \(\frac{1}{\omega C}\) y, a medida que la frecuencia angular aumenta, la impedancia disminuye.
Dado que la fase de la impedancia es la diferencia de fase entre las ondas sinusoidales de voltaje y corriente, en el caso de un capacitor, esta es de \(-90°\), lo que se representa como \(-i\) en números complejos. Por lo tanto, la forma compleja de la impedancia de un capacitor es \(\frac{-i}{\omega C}\).
Como ejemplo práctico, si tenemos un capacitor de desacople ideal de 10 nF, su impedancia a \(1 kHz\) sería de aproximadamente \(16 kΩ\). Si la frecuencia disminuye a \(1 Hz\), la impedancia sería aproximadamente de \(16 MΩ\).
Impedancia de un inductor ideal en el dominio de frecuencia
Para un inductor ideal en el dominio de frecuencia, aplicamos una corriente sinusoidal, lo que genera un voltaje como sigue:
Cuando la amplitud de la corriente es constante, un aumento en la frecuencia resulta en un voltaje mayor en los extremos del inductor. Esto significa que la impedancia del inductor aumenta con la frecuencia y se puede expresar mediante la definición de impedancia como:
Debido a las características del inductor, a medida que la frecuencia aumenta, se vuelve más difícil para la corriente alterna fluir a través del inductor.
Similar al capacitor, la fase de la impedancia del inductor es de \(+90°\), representada como \(i\) en números complejos. La forma compleja de la impedancia del inductor es \(Z=i\omega L\).
En aplicaciones prácticas, la forma y el encapsulado de un capacitor de desacople real pueden introducir inductancia parásita, que es aproximadamente de \(2 nH\). Si consideramos este componente como un inductor ideal, su impedancia a \(1 GHz\) sería de alrededor de \(12Ω\). En comparación, la impedancia de un capacitor ideal sería solo de \(0.01Ω\) a la misma frecuencia, lo que sugiere que a altas frecuencias, un capacitor real puede comportarse como inductancia.
Referencias y Agradecimientos
- "Signal Integrity and Power Integrity Analysis"
Por supuesto, aquí está la traducción al español:
Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.