Integridad de la señal: Dominio del tiempo y Dominio de frecuencia
En general, analizamos las señales desde dos perspectivas distintas: el dominio del tiempo y el dominio de la frecuencia.
Dominio del Tiempo
El dominio del tiempo es la representación de la señal tal como se presenta en el mundo real, secuencialmente en función del tiempo. Por ejemplo, en el gráfico del dominio del tiempo de una señal de reloj, podemos observar dos parámetros importantes: el período de la forma de onda y el flanco de subida:
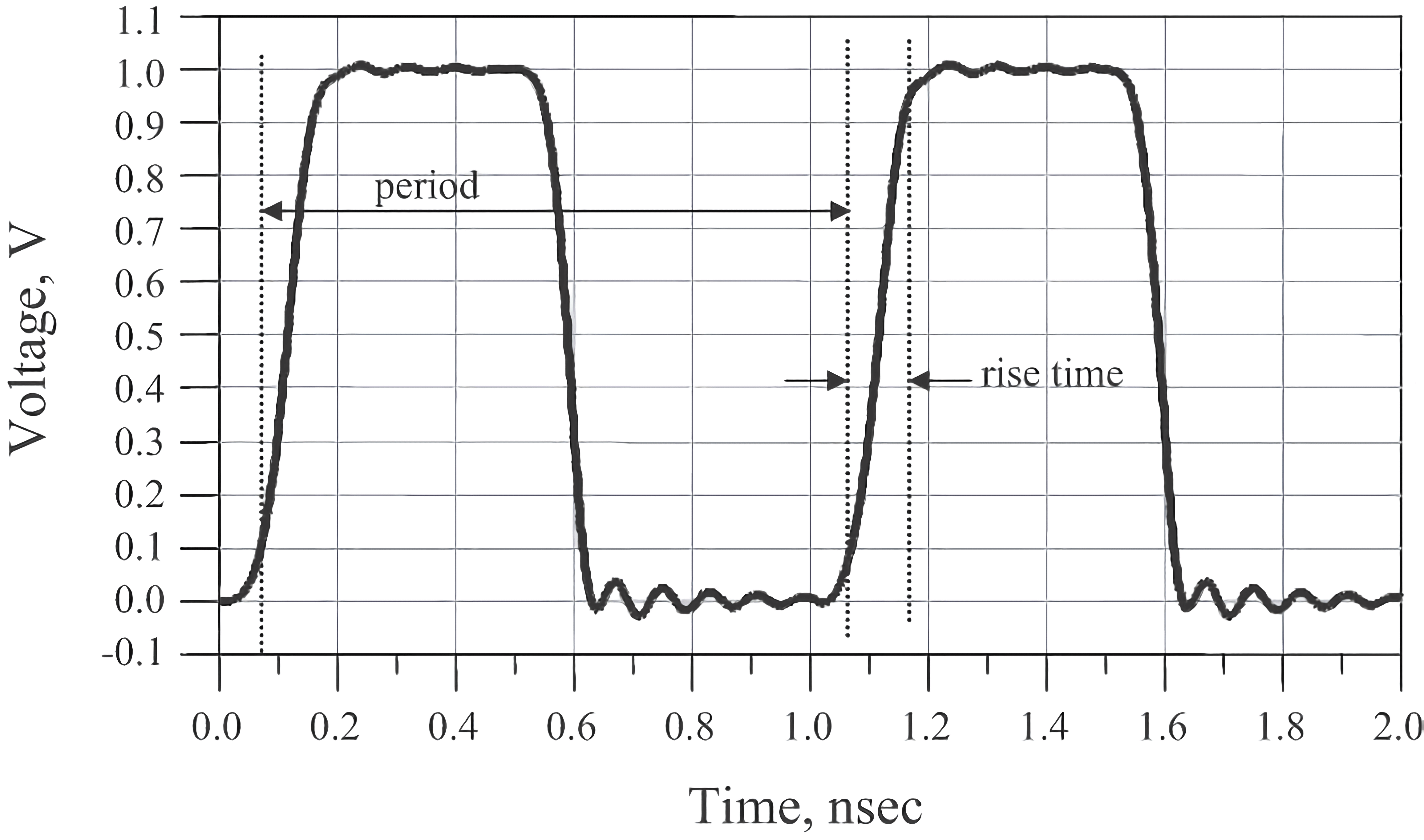
El período de un reloj es el tiempo que toma la señal para repetirse una vez, generalmente se mide en nanosegundos. La frecuencia del reloj es simplemente el inverso del período, es decir, si el período es de 1 ns, la frecuencia es de 0.1 GHz.
El flanco de subida se define comúnmente como el tiempo que lleva que la señal pase del 20% al 80% de su nivel máximo (a veces se define como del 10% al 90%). Los flancos de bajada suelen ser más cortos que los de subida debido a que en estructuras CMOS típicas, los transistores N-MOS conducen más rápido que los P-MOS, lo que hace que los flancos de bajada sean más cortos y más propensos a problemas de integridad de la señal.
Dominio de Frecuencia
El dominio de la frecuencia es un concepto matemático. En este dominio, las ondas senoidales se utilizan comúnmente porque cualquier forma de onda en el dominio del tiempo se puede descomponer en ondas senoidales.
El dominio de la frecuencia permite describir la misma información de manera más concisa. Como se muestra en la siguiente imagen, en la izquierda se describe una onda senoidal en el dominio del tiempo, que se puede caracterizar completamente por sus tres parámetros: frecuencia, amplitud y fase. En cambio, en la derecha, en el dominio de la frecuencia, solo se requiere un punto para representar la frecuencia y la amplitud (generalmente se ignora la fase en la mayoría de los casos):
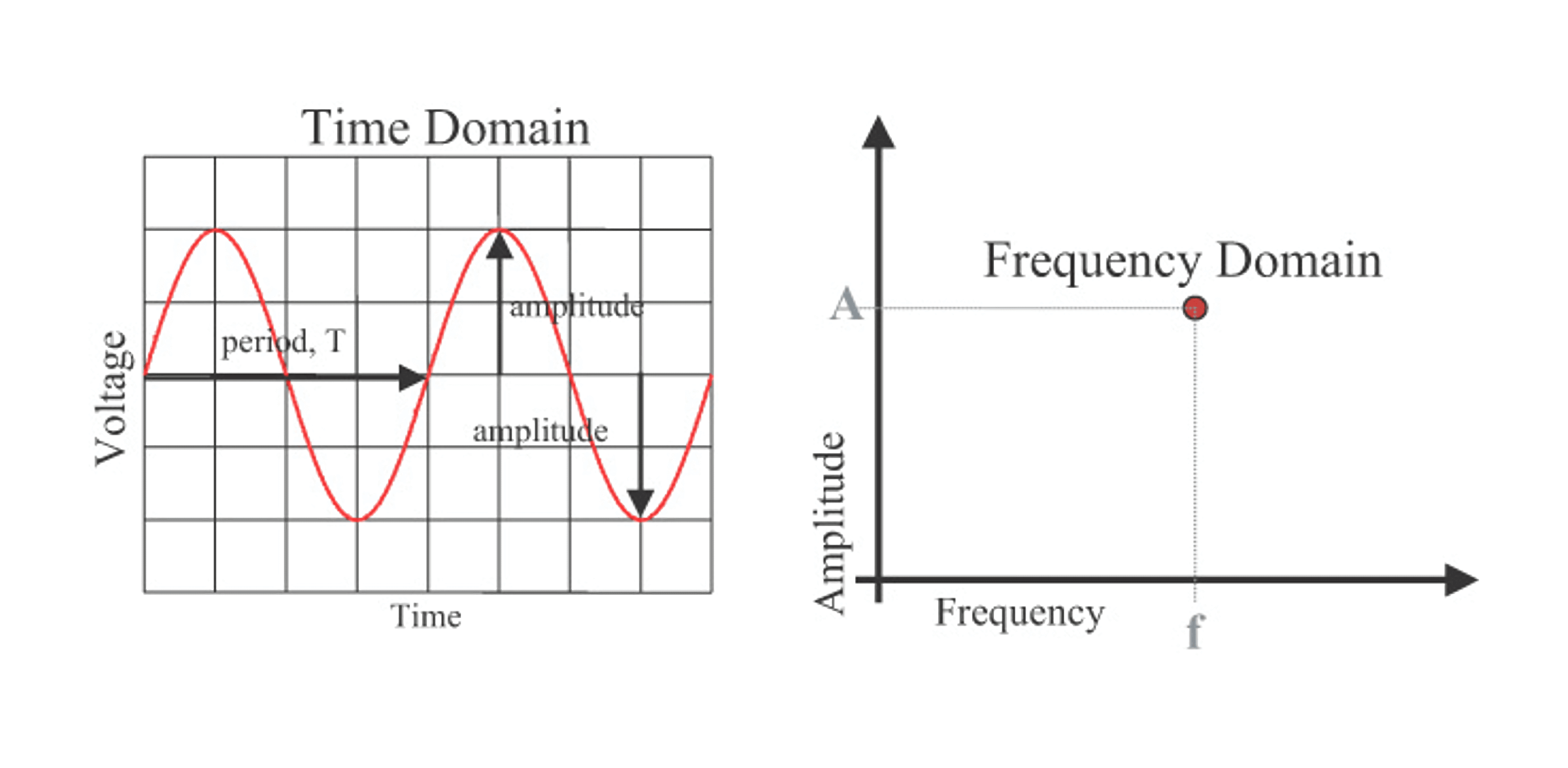
De esta manera, una onda senoidal se representa en el dominio de la frecuencia con un solo punto. Si hay varios puntos de frecuencia, este conjunto se conoce como un espectro de frecuencia.
Al abordar problemas eléctricos de interconexión en el dominio de la frecuencia y utilizando ondas senoidales para describirlos, resulta más fácil comprender y resolver los problemas.
Transformación del Dominio del Tiempo al Dominio de la Frecuencia
Para transformar del dominio del tiempo al dominio de la frecuencia, se utiliza la transformada de Fourier. Existen tres tipos de transformadas de Fourier: la transformada integral de Fourier (FI), la transformada discreta de Fourier (DFT) y la transformada rápida de Fourier (FFT).
La transformada de Fourier se utiliza para convertir una expresión matemática ideal en el dominio del tiempo en una representación en el dominio de la frecuencia, integrando desde menos infinito hasta más infinito a lo largo del eje del tiempo en el dominio del tiempo para obtener una función de frecuencia continua desde cero hasta más infinito.
Sin embargo, en la práctica, las formas de onda en el dominio del tiempo suelen estar compuestas por una serie de puntos discretos. En este caso, la transformada discreta de Fourier se utiliza para transformar la forma de onda al dominio de la frecuencia (siempre que la señal en el dominio del tiempo sea periódica). A diferencia de la transformada de Fourier integral, la transformada de Fourier discreta se calcula simplemente sumando los valores.
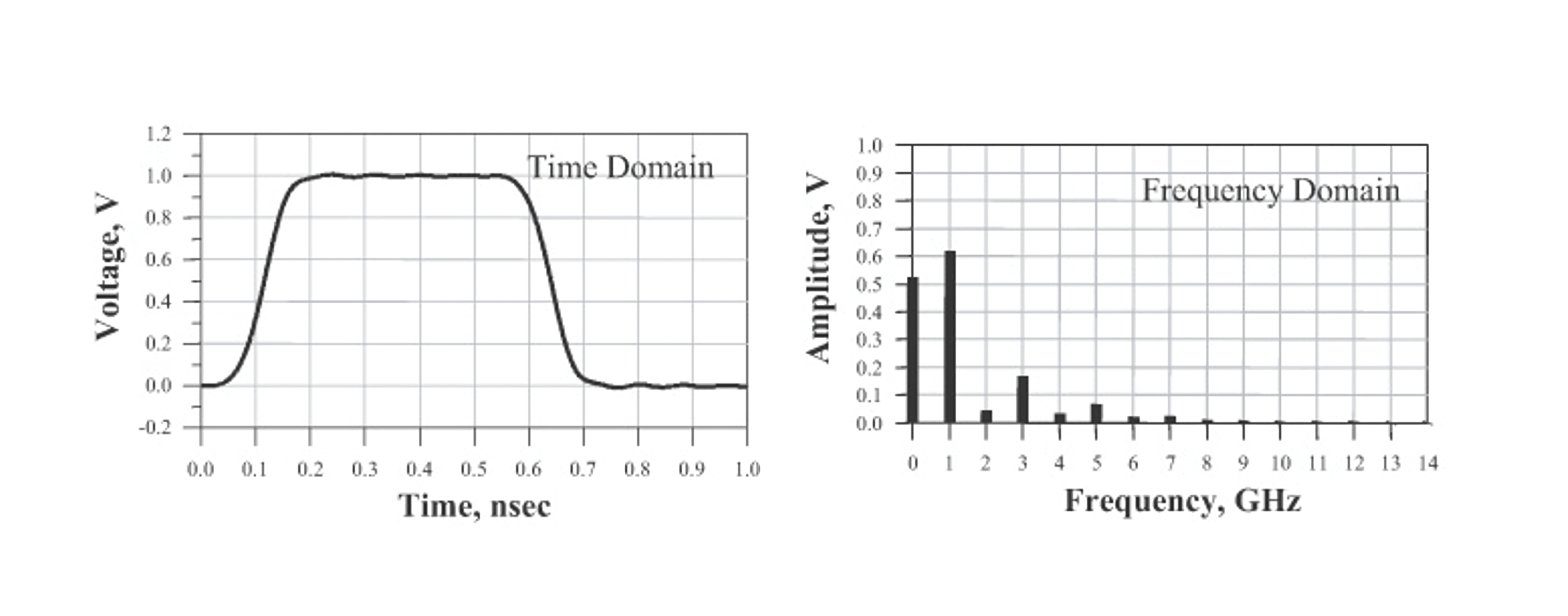
La transformada rápida de Fourier utiliza métodos de álgebra matricial rápida y se aplica en casos donde el número de puntos de datos en el dominio del tiempo es una potencia de dos (por ejemplo, 256, 512, 1024 puntos). Dependiendo del número de puntos de datos, la FFT puede ser significativamente más rápida que la transformada discreta de Fourier convencional.
Es importante señalar que la FFT requiere que la señal sea periódica, por lo que se debe muestrear coherentemente la señal original o aplicar ventanas después del muestreo.
Transformación Inversa del Dominio de Frecuencia al Dominio del Tiempo
El dominio de frecuencia contiene información sobre las frecuencias y amplitudes de todas las componentes senoidales en una forma de onda. Si se desea obtener la forma de onda en el dominio del tiempo, solo se necesita realizar una transformación inversa de Fourier multiplicando cada componente de frecuencia por su correspondiente forma de onda senoidal en el dominio del tiempo y sumándolas, un proceso conocido como la transformada inversa de Fourier.
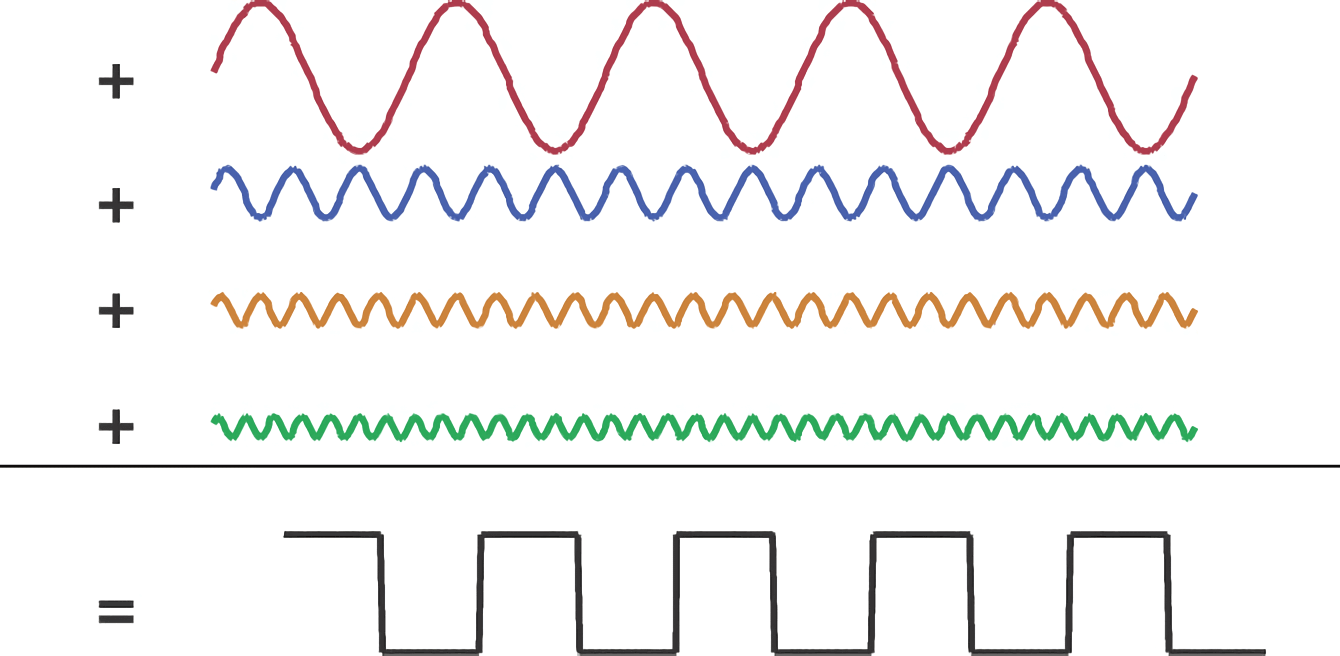
Un ejemplo notable de esto es la forma de onda cuadrada, que se compone de múltiples componentes armónicas senoidales. Cuantas más componentes se sumen, más empinado será el flanco de subida y más se asemejará a una forma de onda cuadrada ideal.
Ancho de Banda y Flanco de Subida
El ancho de banda se refiere a la frecuencia de la componente senoidal más alta y efectiva en el espectro de frecuencia (ya que en señales digitales, la frecuencia más baja siempre es continua, es decir, igual a cero). Representa el rango de frecuencias en el espectro de la señal. La elección del ancho de banda tiene un impacto directo en el flanco de subida más corto en la forma de onda en el dominio del tiempo. Tomando como ejemplo una forma de onda cuadrada ideal, cuanto mayor sea el ancho de banda, más corto será el flanco de subida, y la forma de onda se acercará más a una forma de onda cuadrada ideal.
Es importante destacar que "efectiva" significa que la amplitud de la componente armónica en la señal debe ser superior al 70% de la amplitud de la componente armónica correspondiente
De acuerdo con la regla empírica derivada de experimentos, la relación entre el ancho de banda y el tiempo de subida es \(BW=\frac{0.35}{RT}\), donde BW es el ancho de banda (GHz) y RT es el tiempo de subida del 10% al 90% (ns). Por ejemplo, si el tiempo de subida de la señal es de 0.1 ns, entonces el ancho de banda de la señal es de 0.35 GHz, y lo mismo es cierto en sentido inverso. (Ten en cuenta que las unidades corresponden, GHz corresponde a ns, MHz corresponde a us).
Referencias y Agradecimientos
- "Signal Integrity and Power Integrity Analysis"
- Explicación visual de la serie de Fourier y la transformada de Fourier
- Serie básica sobre la Transformada de Fourier
Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.