Calculation of Solar Altitude Angle
To represent the position of the sun in the sky, it is necessary to first choose a coordinate system. The two commonly used coordinate systems are the equatorial coordinate system and the horizontal coordinate system.
Concepts:
- Latitude \(\varphi\): -90° to 90°, with positive values for northern latitudes.
Equatorial Coordinate System
The equatorial coordinate system takes the celestial equator as the fundamental plane and defines the position of the sun using two quantities: declination angle and hour angle.
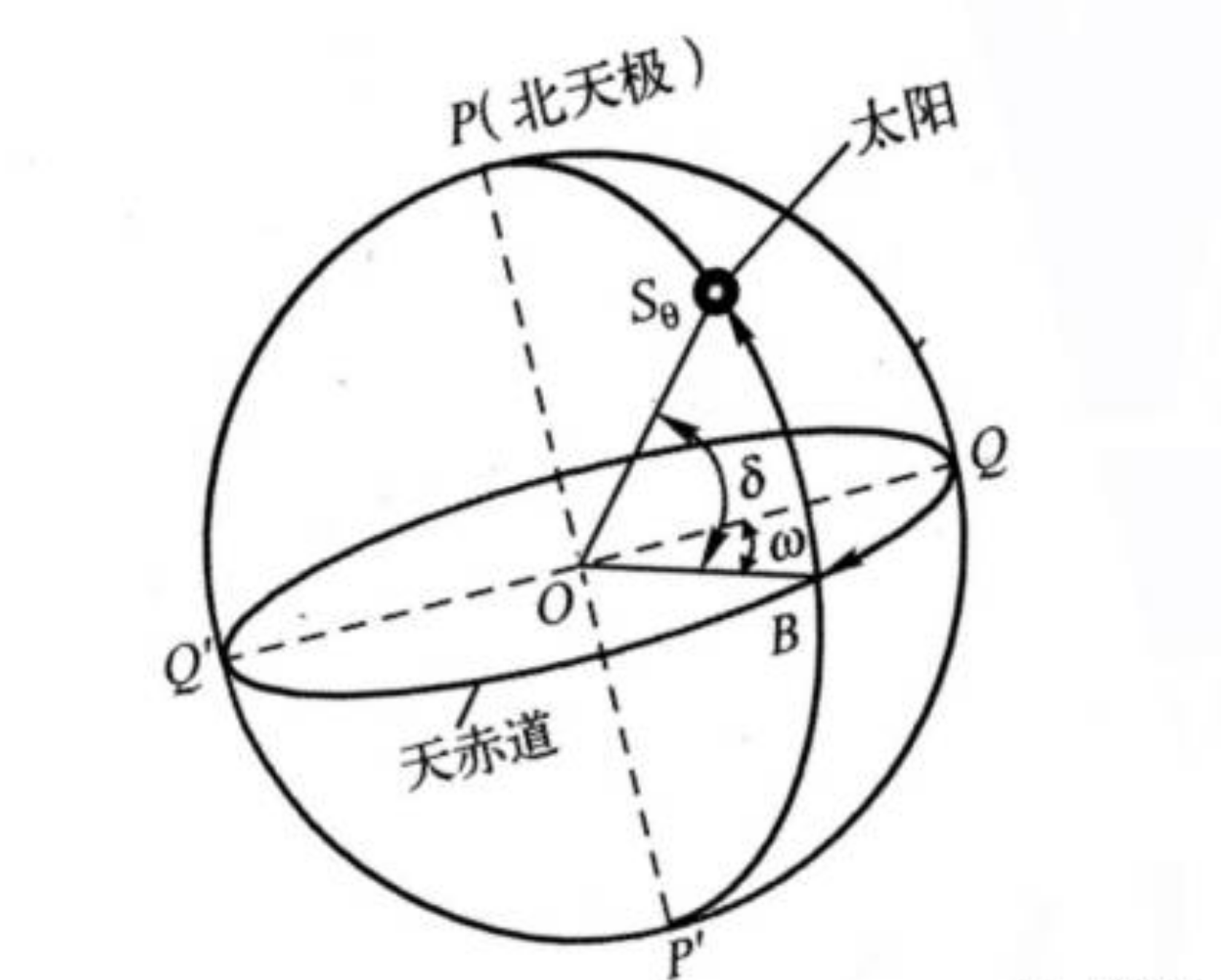
- Declination angle \(\delta\): The angle between the line connecting the Earth and the sun and the celestial equator.
- Hour angle \(\omega\): Negative in the morning, positive in the afternoon, numerically equal to the time (in hours) from noon multiplied by 15°.
The declination angle varies between the Tropic of Cancer and the Tropic of Capricorn (-23.45° to 23.45°) due to the position of the Earth in its orbit:
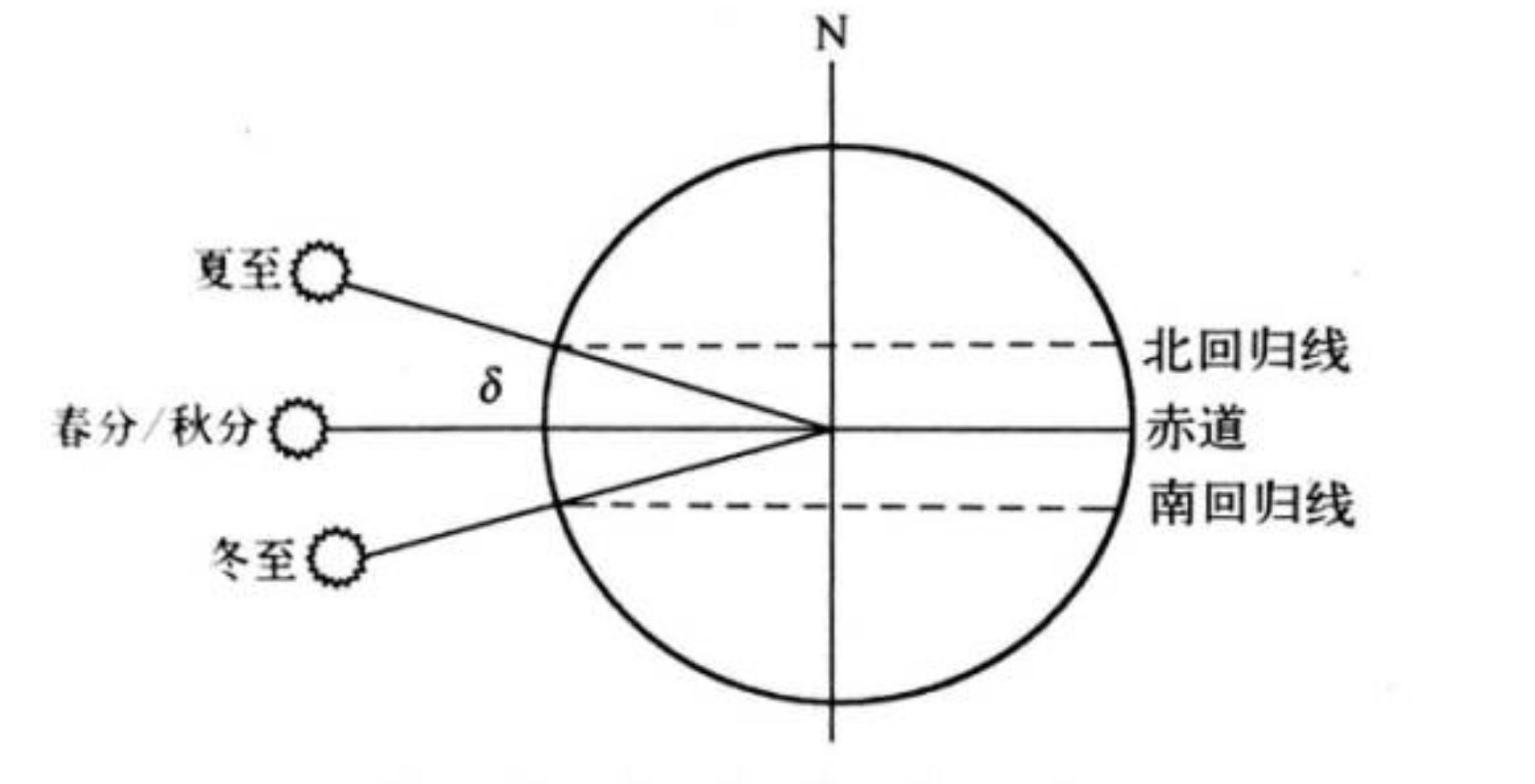
The formula to calculate the declination angle \(\delta\) is as follows:
where n is the date number within a year (1 to 365).
Horizontal Coordinate System
The horizontal coordinate system takes the observer's horizon as the fundamental plane. In this coordinate system, we use the altitude angle and azimuth angle to define the position of the sun in the sky at a specific moment.
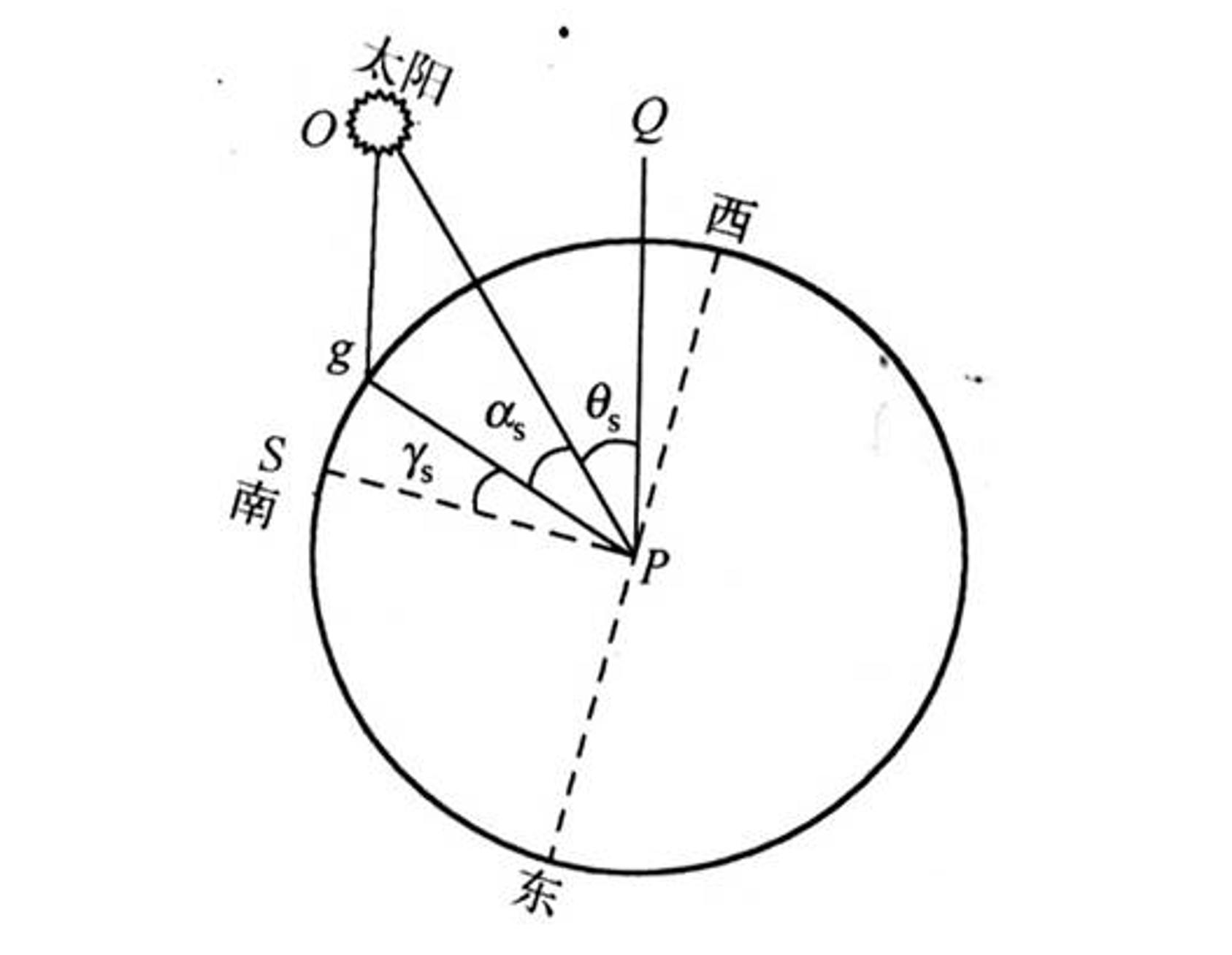
Note: To understand this diagram, you need to have a geometric imagination, imagining that the circle is on a flat surface and the sun is above the surface.
- Altitude angle \(\alpha_s\): The angle between the line connecting the sun's rays and the observer and the projection of this line on the ground.
- Azimuth angle \(\gamma_s\): The angle between the projection of the line connecting the sun's rays and the observer on the ground and the line pointing due south. The numerical value is 0° for due south, positive for westward direction, and negative for eastward direction.
The formula to calculate the altitude angle \(\alpha_s\) is:
The formulas to calculate the azimuth angle \(\gamma_s\) are:
Standard Time and Solar Time
Standard time refers to the civil time (e.g., Beijing Time), while solar time is based on noon (12:00) as the reference time.
For example, in Beijing and Urumqi, the highest solar altitude occurs at solar noon (12:00). However, in standard time, the highest solar altitude in Urumqi (i.e., noon) is around 14:00.
References and Acknowledgements
- Mastering Geographical Knowledge in Photovoltaic Systems
- Latitude and Longitude Lookup
- Solar calculator
- Design of Solar Tracking System for Photovoltaic Power Generation
- [AngleCalculations.pdf]
Original: https://wiki-power.com/
This post is protected by CC BY-NC-SA 4.0 agreement, should be reproduced with attribution.This post is translated using ChatGPT, please feedback if any omissions.