أساسيات اختبار الإشارة المختلطة
الإشارة المختلطة تحتوي على إشارات تناوبية ورقمية معًا. الأجهزة التي تعالج الإشارة المختلطة تتضمن عادة محولات تناوب إلى رقمي (ADCs)، محولات رقمي إلى تناوب (DACs)، ومفاتيح تناوبية ومضاعفات، ومكبرات العينة والاحتفاظ بالعينات، وما إلى ذلك.
كجزء من ذلك، الإشارات التناوبية هي الإشارات التي نستخدمها في العالم الحقيقي مثل الصوت أو درجة الحرارة، وهي مستمرة من حيث الزمن والشدة. لمعالجة الإشارات التناوبية في الحواسيب، نحتاج إلى تحويلها إلى إشارات رقمية، حيث تكون متقطعة من حيث الزمن والشدة.
نظرية العينة
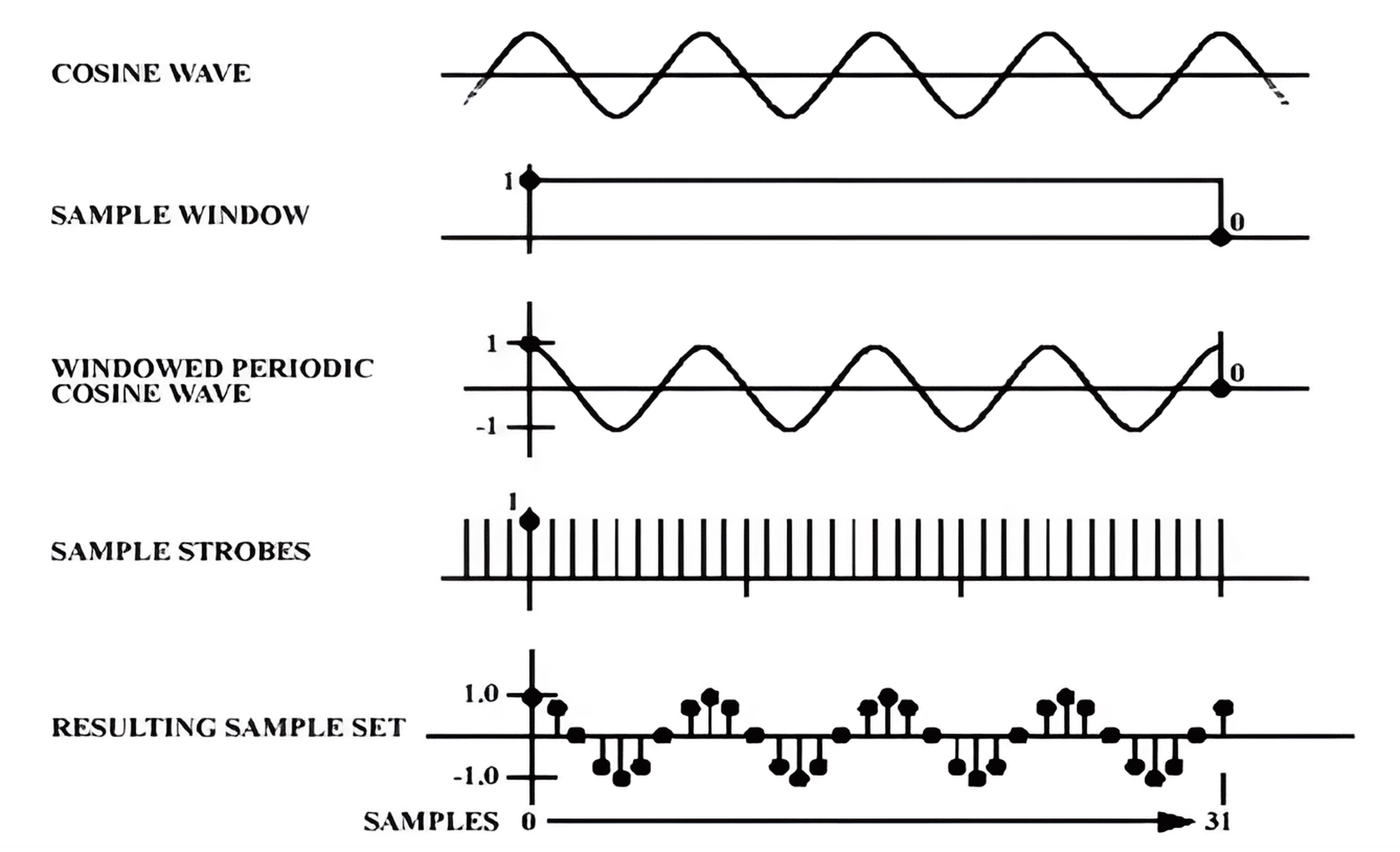
تنطبق نظرية العينة على الإشارة عندما تكون تناوبية، أو ستتم إدخال أخطاء.
نظرية نايكويست
نحن نستخدم نظرية نايكويست (奈奎斯特定理) للحصول على التردد الأدنى اللازم للعينة عند عينة الإشارات:
يجب أن نقوم بعينة بتردد أعلى من ضعف أعلى تردد مهتم به، لنكون قادرين على إعادة بناء الإشارة من عيناتها وتجنب فقدان المعلومات.
إذا قمنا بعينة بتردد أقل من تردد نايكويست، سيظهر ظاهرة تسمى التداخل (混叠) عند محاولتنا تحويلها مرة أخرى إلى إشارة زمنية مستمرة، وبعض الترددات في الإشارة الأصلية قد تتضائل.
للحد من مشكلة التداخل، نحتاج إلى إزالة التردد الأعلى من \(\frac{F_s}{2}\) من الإشارة، من خلال مرشح مضاد للتداخل (على سبيل المثال، مرشح منخفض المرور):
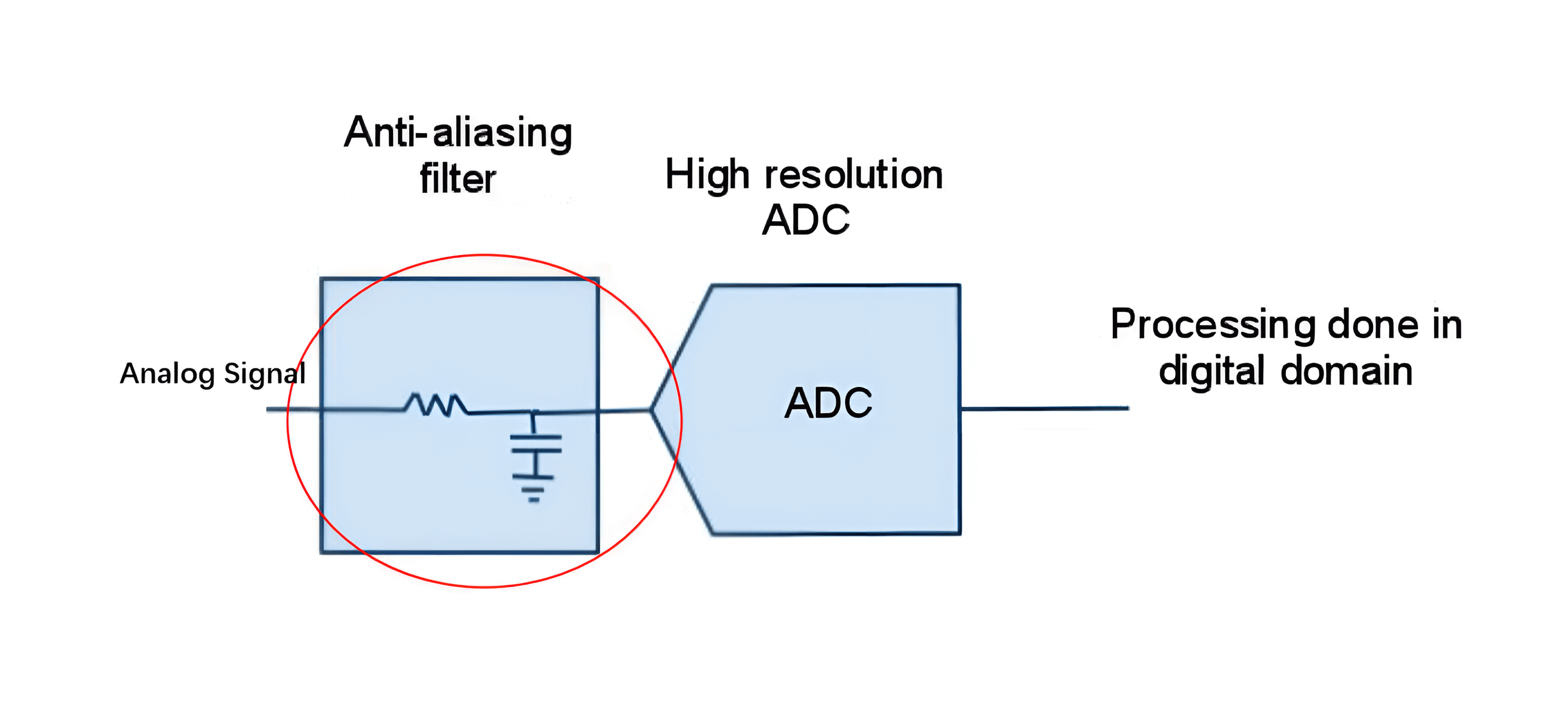
عينة متماسكة
إذا لم تحتوي مجموعة العينات الزمنية على عدد صحيح دقيق من الدورات، ستحدث تسرب طيفي (频谱泄露).
العينة المترابطة (Coherent Sampling) تهدف إلى ضمان استمرارية عملية العينة ومنع تسرب الطيف، حيث تضمن أن مجموعة العينات (سلسلة من العينات التي تمثل الإشارة التمثيلية) تحتفظ بعلاقة ثابتة ومحددة بين تردد العينة \(F_s\)، وعدد العينات \(N\)، وتردد الإشارة التجريبية \(F_i\)، وعدد فترات الإشارة التجريبية المعمول بها \(M\):
$$ \frac{M}{N}=\frac{F_i}{F_s}
الوقت الإجمالي المطلوب لأخذ جميع العينات يُسمى **فترة الاختبار الوحدية (UTP)** وتحتاج إلى $M$ دورة من الإشارة التجريبية، التي تمتلك تردد $F_i$.
على سبيل المثال، إذا أردنا حساب تردد العينة $F_s$ لموجة جيب متكررة باستمرار، حيث يكون $F_i$ هو 1 كيلو هرتز، و$M=3$ و$N=16$:
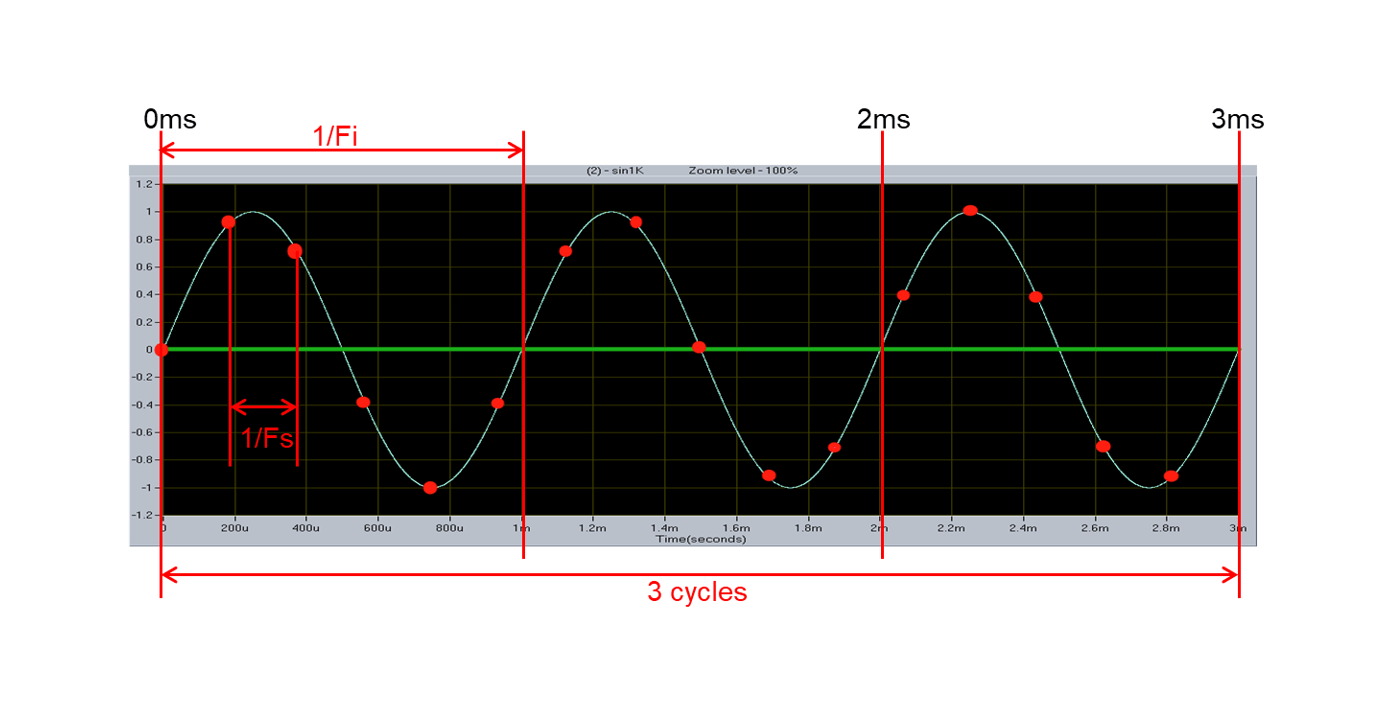
لذا يمكننا الاستنتاج أن $F_s=5.333 كيلو هرتز$.
نصائح مهمة حول العينة المترابطة:
- زيادة قيمة $M$ و/أو $N$ ستزيد من دقة الاختبار ووقت الاختبار.
- $M$ و$N$ يجب أن تكونا عبارة عن أعداد صحيحة.
- يجب أن يكون $N$ عبارة عن قوة للعدد 2 عند استخدام تحليل فوريي سريع (FFT).
- يُفضل أن تكون $M$ و$N$ متبادلة الأعداد الأولية (متبادلة) حتى تعطي كل عينة معلومات فريدة. يُوضح ذلك فيما يلي.
إذا كانت $M$ و$N$ ليستا متبادلتين الأعداد الأولية ($M=3,N=12$)، يتم أخذ العينات في نفس الموقع في كل دورة، لذا لن توفر معلومات جديدة:
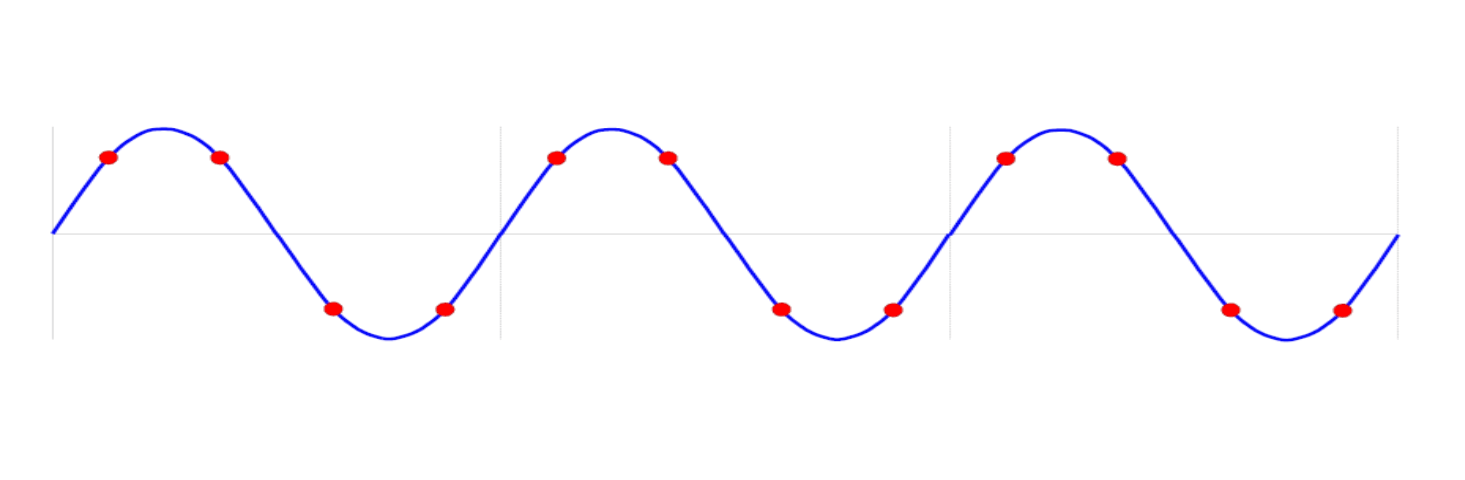
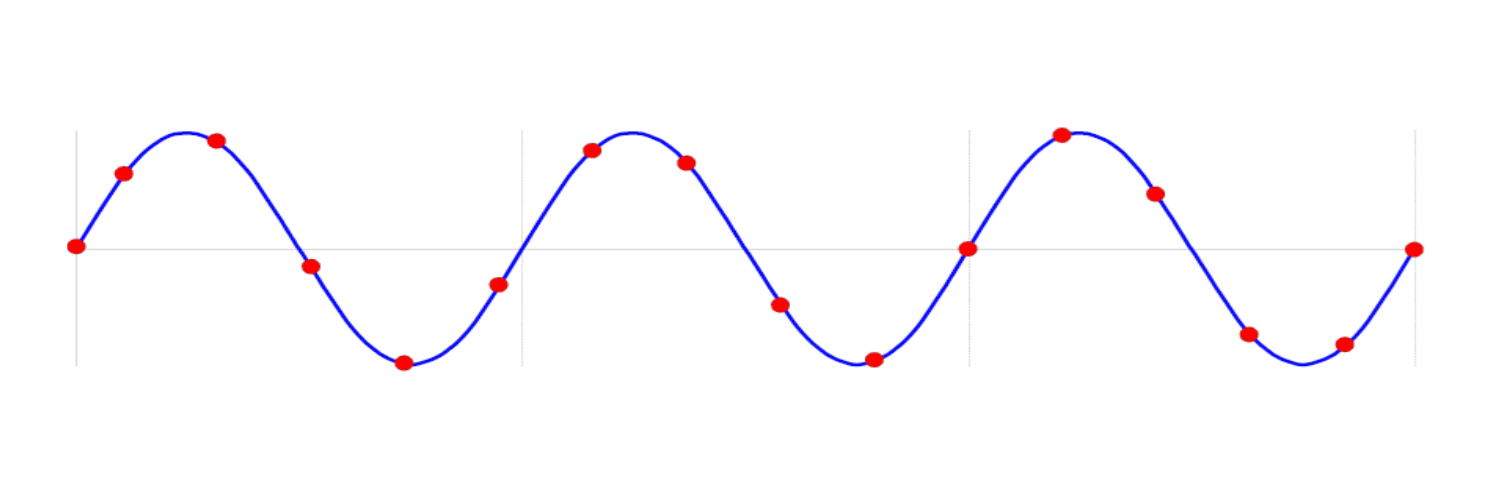
إذا كانت $M$ و$N$ متبادلتين الأعداد الأولية ($M=3,N=16$)، فإنها متبادلتين الأعداد الأولية وكل عينة تكون منفصلة، مما يمنح معلومات فريدة:
## خوارزميات تحليل التردد المشتركة
لعدد $N$ من عينات إشارة المجال الزمني، هناك $N$ قيم لإشارة المجال الترددي، وهناك قيم قدرة مجال ترددي بنسبة $N/2$. مثال نموذجي لمكونات الطيف يُعرض أدناه:
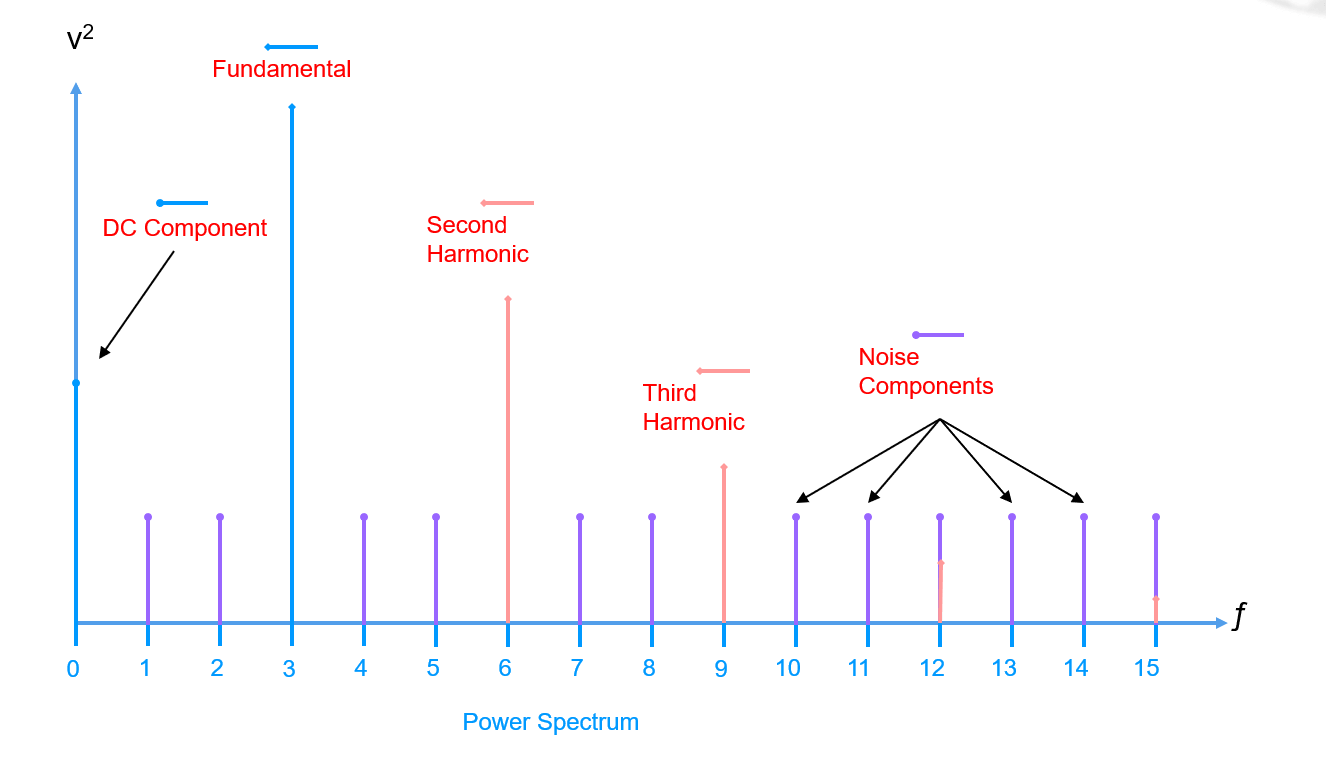
هناك عدة معاملات لوصف مكونات الطيف كما يلي:
- نسبة إشارة إلى ضوضاء (SNR)
- الانحراف التوافقي الكلي (THD)
- نسبة الإشارة إلى الضوضاء والتشويش (SINAD)
- الانحراف بين الانمزاغات (IM)
- نطاق دينامي مجاني من الاشارات الزائدة (SFDR)
### نسبة إشارة إلى ضوضاء (SNR)
**نسبة إشارة إلى ضوضاء (SNR)** تُشتق بالبداية من تخزين قيمة الأساسية (قدرة الإشارة) أولاً:
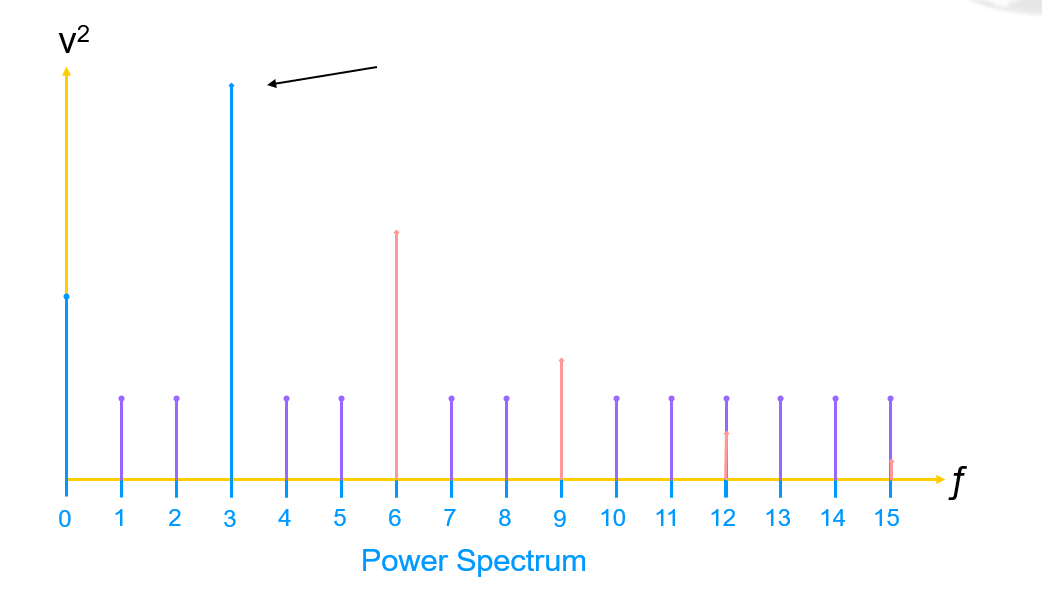
ثم تزيل المكون المستمر والترددات المتعددة (عادة حتى النماذج الخمسة الأولى):
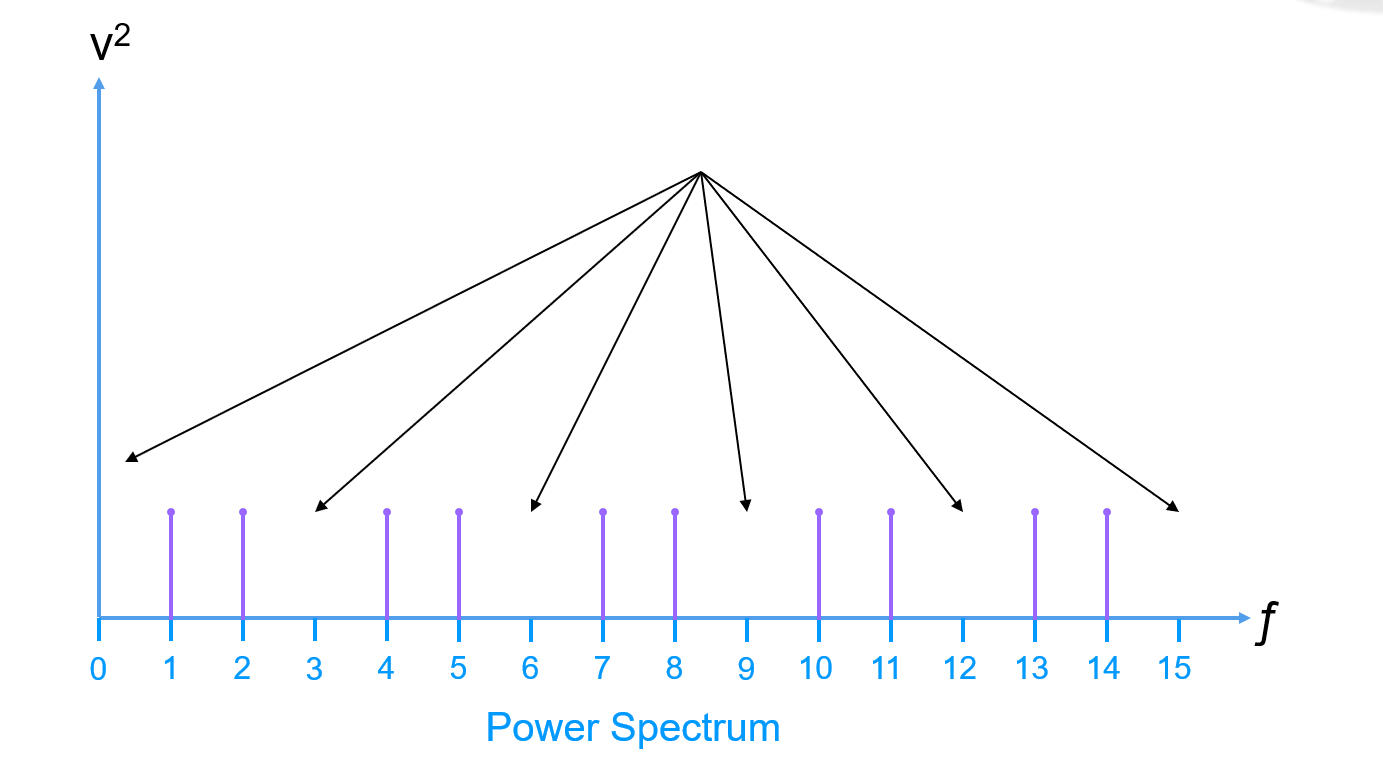
ثم تقوم بجمع جميع أقسام القدرة المتبقية في مجال التردد (قدرة الضوضاء) والتي يتم قياسها بواسطة القيمة الجذرية المتوسطة (الجهد التماثلي الذي يكون مساويًا لجهد التيار المستمر الذي يحتوي على نفس كمية الطاقة، بالنسبة لموجة السينوس، القيمة الجذرية المتوسطة هي مرة واحدة على 0.707 من القيمة القصوى):
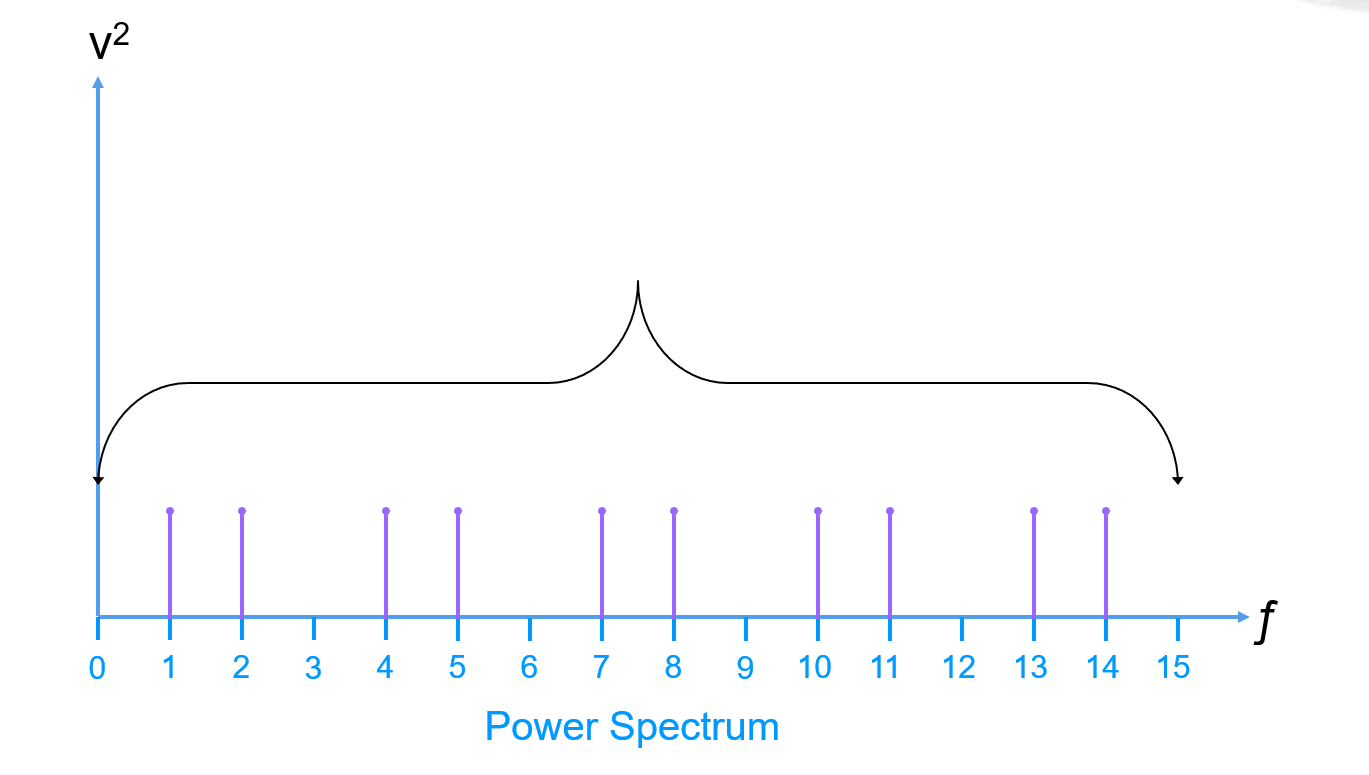
في النهاية، يمكننا الختام أن:
$$
{SNR}(dB)=10log\_{10}(\frac{{الأساسية}}{{قدرة\ الضوضاء}})
$$
نسبة الإشارة إلى الضوضاء عادة ما تُعبَّر بوحدة الديسيبل (dB)، وغالبًا ما تكون قيمة إيجابية (بشرط أن تكون قدرة الأساسية أكبر بكثير من قدرة الضوضاء).
### الانحراف التوافقي الكلي (THD)
**الانحراف التوافقي الكلي (THD)** يُشتق من خلال الاحتفاظ بمجموع تردد الهارمونيات الكلي (عادة فقط الهارمونيات الخمسة الأولى، ابتداءً من التردد الثاني):
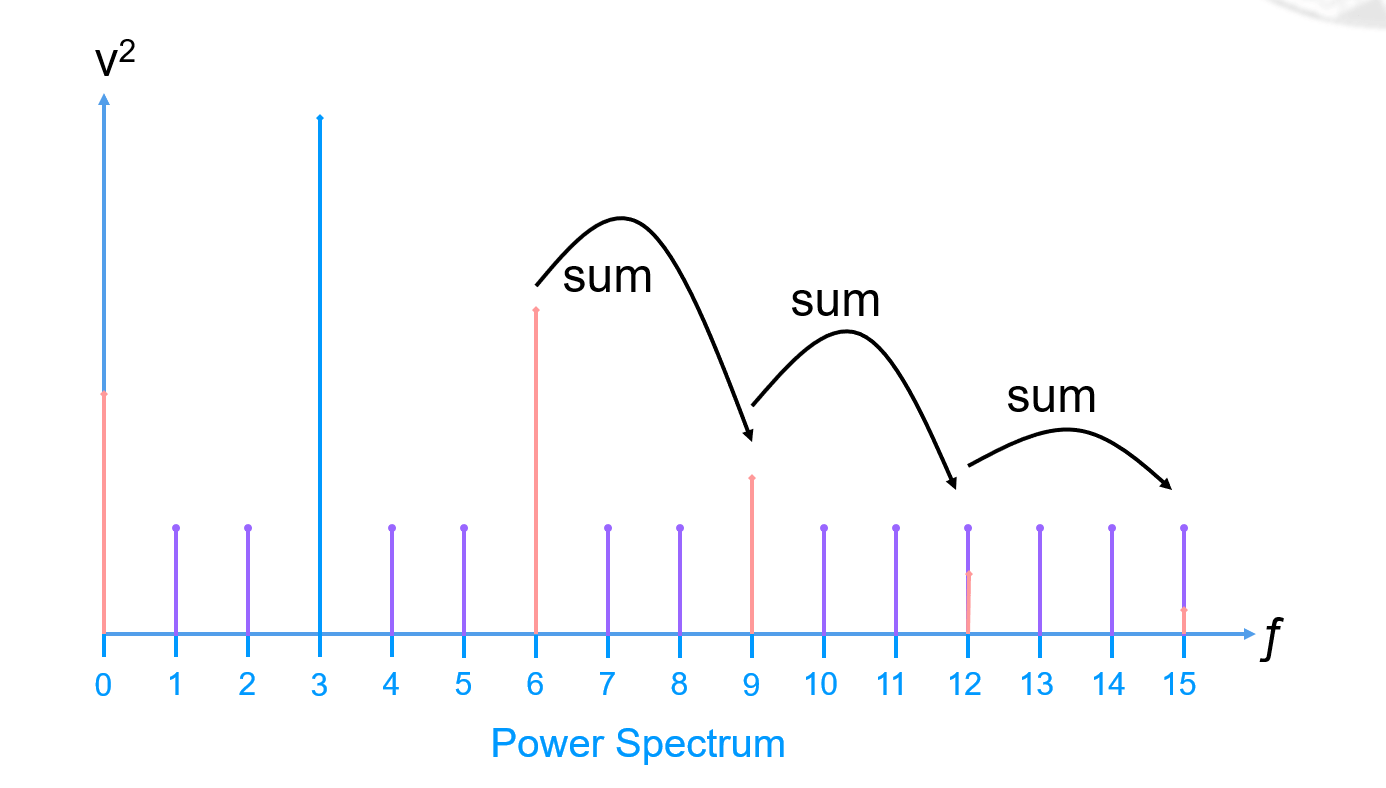
ونستنتج ما يلي:
```markdown
$$
{THD}(dB)=10\log\_{10}\left(\frac{{الطاقة \ الموجهة}}{{الأساسية}})
$$
THD غالبًا ما تكون قيمتها سالبة (بشرط أن تكون قوة الأساسية أكبر بكثير من إجمالي قوة الموجهات).
### نسبة الإشارة إلى الضوضاء والتشويش (SINAD)
**نسبة الإشارة إلى الضوضاء والتشويش (SINAD)** هي نفس منهجية حساب نسبة الإشارة إلى الضوضاء (SNR)، لكن الآن تمتزج فيها قوة الموجهات فقط ويتم تجاهل مكون التيار المباشر (DC).
$$
{SINAD}=\frac{S}{N+D}
$$
ويمكننا الاستنتاج من ذلك:
$$
\لأن{SNR}=\frac{S}{N}, {THD}=\frac{D}{S}
$$
$$
\لذلك{SNR}^{-1}+{THD}=\frac{N}{S}+\frac{D}{S}=\frac{N+D}{S}={SINAD}^{-1}
$$
$$
\لذلك{SINAD}=({SNR}^{-1}+{THD})^{-1}
$$
### التشويش بين الإشارات (IM)
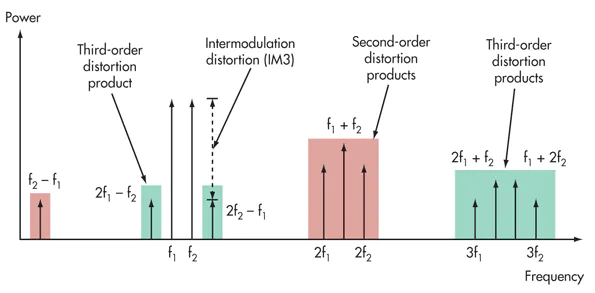
يحدث التشويش بين الإشارات (IM) عندما يتم استخدام إشارتين أو أكثر في نظام غير خطي. سيتضمن الطيف ليس فقط الإشارات الأصلية، ولكن أيضًا مجموع وفارق الإشارات المدخلة مع مضاعفاتها.
### نطاق الديناميكية الحرة من التشويش (SFRD)
**نطاق الديناميكية الحرة من التشويش (SFRD)** يتم تحقيقه عن طريق العثور على أعلى عنصر بعد الإشارة الأساسية (بتجاهل مكون التيار المباشر):
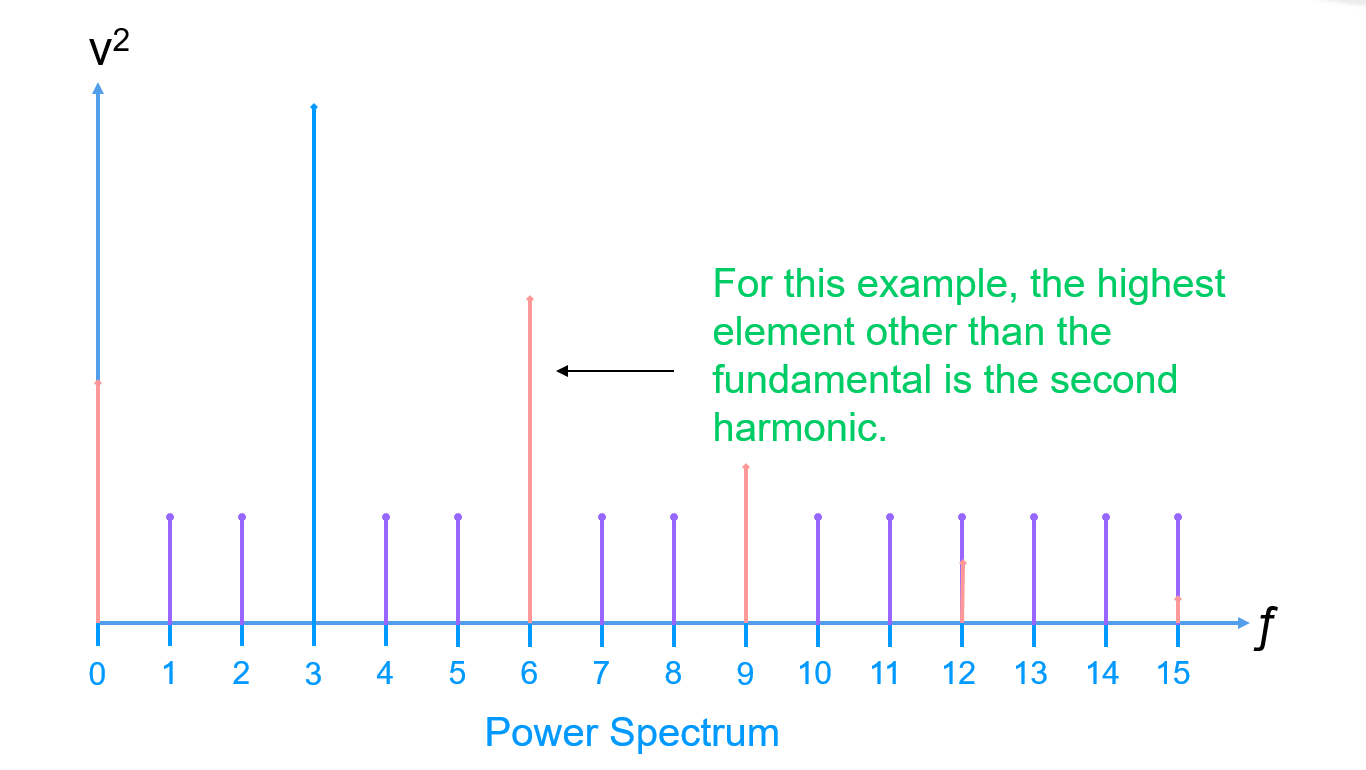
لاحظ أن أعلى عنصر قد يكون أو لا يكون موجهة. لذلك يمكننا الاستنتاج من ذلك:
$$
{SFDR}(dB)=10\log\_{10}\left(\frac{{الأساسية}}{{أعلى \ أعلى \ تالي}})
$$
نطاق الديناميكية الحرة من التشويش هو قيمة إيجابية (بشرط أن تكون قوة الأساسية أكبر بكثير من قوة التشويش الأعلى التالية.
## بنية جهاز اختبار الإشارة المختلطة العام
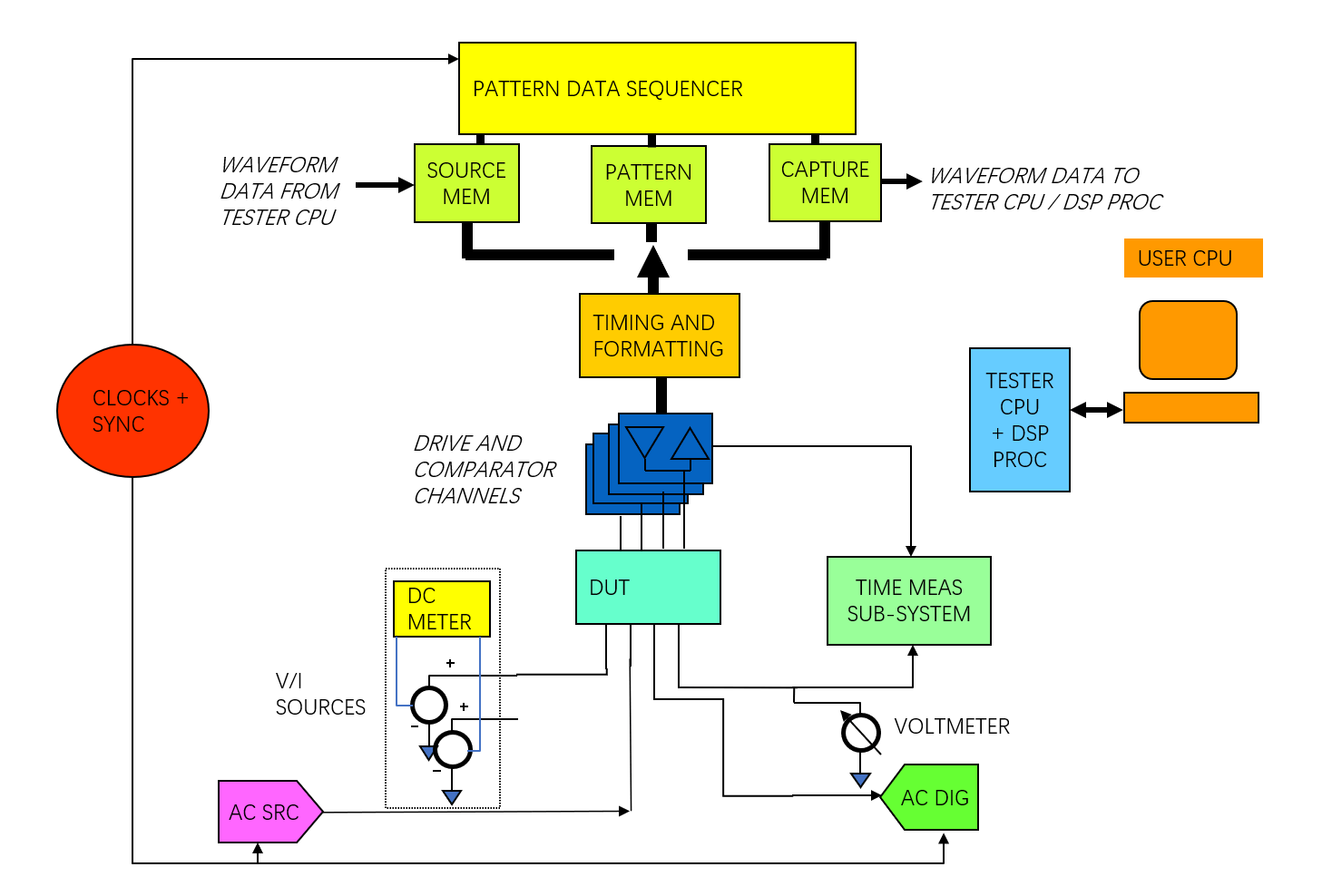
في جهاز اختبار الإشارة المختلطة العام، تكون مولد الإشارة المترددة (AC src) ومحلل الإشارة الرقمية (AC dig) متصلين بجهاز الاختبار عبر توصيلات الريلي عبر لوحة القناة.
مولد موجات تكوينية (AWG)
مولد الموجات التكوينية (AWG) هو مُولِّد إشارة ذات تشويه منخفض. يحتوي على محول رقمي إلى تمثيل إشارة تناظرية من البيانات الرقمية.
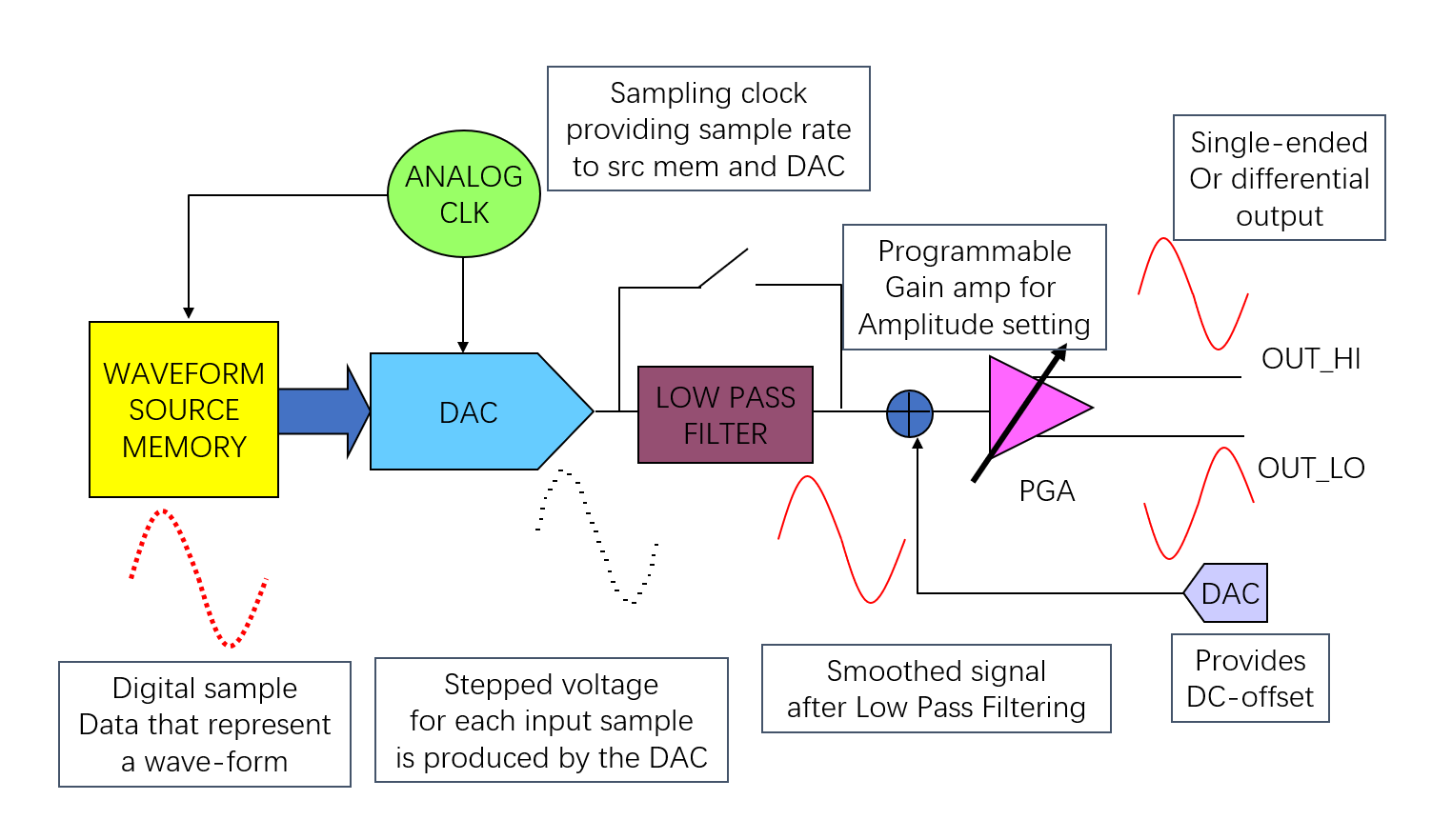
المُرشِّح عابر منخفض التمرير (LPF) يستخدم لتنعيم الشكل الموجي وإزالة المكونات عالية التردد. مجموعة نقاط بيانات لشكل موجة معين تُخزن في ذاكرة مصدر الشكل الموجي، في كل مرة تحدث فيها ساعة، ستُمر نقطة بيانات إلى المحول الرقمي إلى تمثيل إشارة تناظرية.
المعلمات المهمة لـ AWG:
- الحد الأقصى لإخراج الجهد من الذروة إلى الذروة
- دقة الشكل الموجي (دقة المحول الرقمي)
- العرض النطاقي
- عمق ذاكرة مصدر الشكل الموجي
- المقاومة الكهربائية للإخراج
- الضوضاء، الانحراف عن الموجة المثالية، نسبة الإشارة إلى الضوضاء (THD, SNR)
جهاز ترقيم الموجة (WD)
جهاز ترقيم الموجة (WD) يأخذ عينات من الإشارات التناظرية ويحولها إلى قيم رقمية. يقوم بالعملية المعاكسة لما يقوم به مولد الموجات التكوينية. يحول الإشارة التناظرية إلى عينات رقمية تمثل الإشارة التناظرية الأصلية.
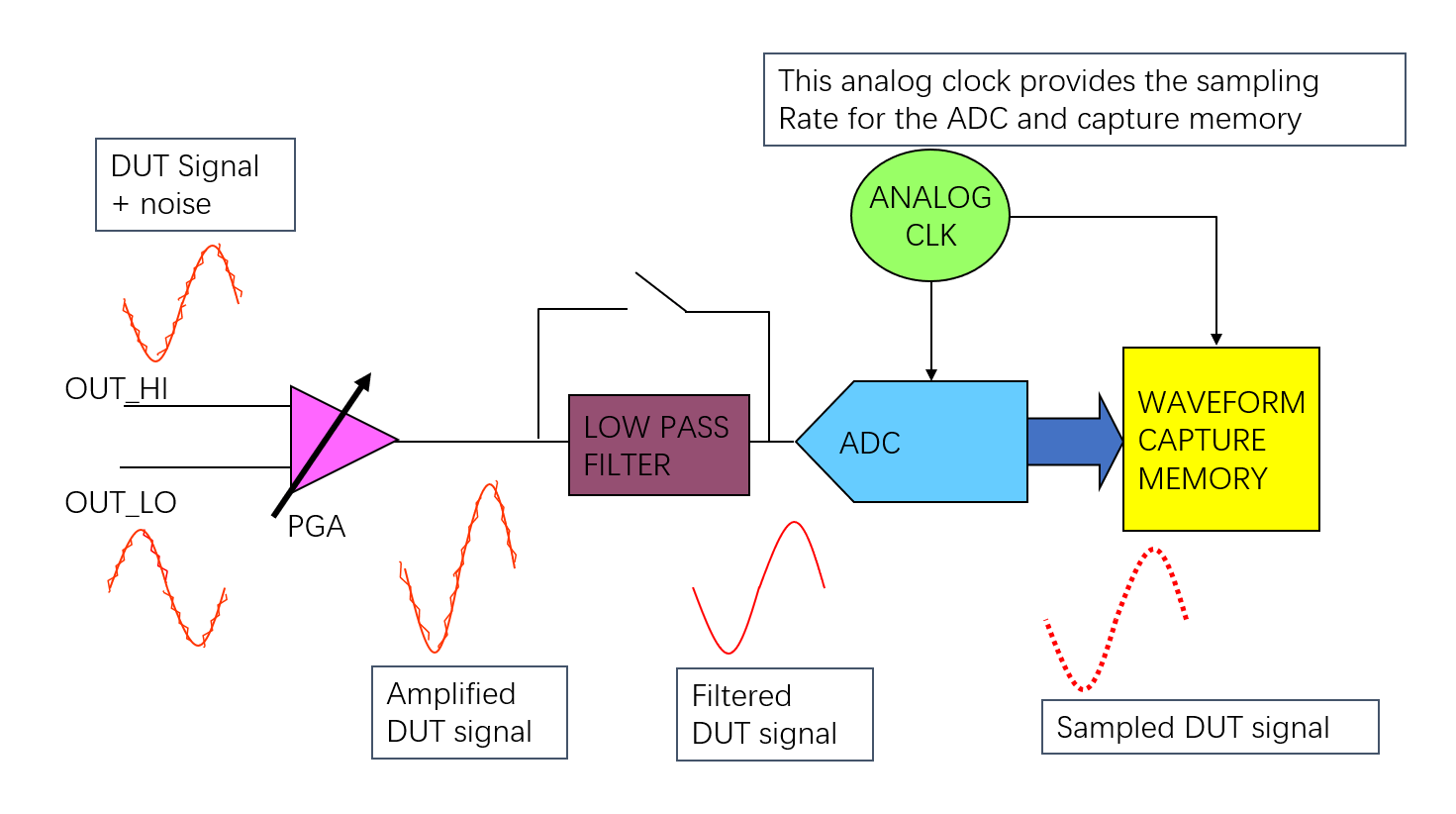
يحدِّد المُرشِّح عابر منخفض التمرير حزمة النطاق الترددي للإشارة من أجل إزالة المكونات ذات الترددات غير المرغوب فيها مثل الضوضاء والاضافات، ويوفر أيضًا حمايةً من تأثير الالياسينج عن طريق تخفيض مستوى الاضافات التي قد تكون قد تم الالياسينج لها داخل نطاق الترشيح أثناء عملية التحويل إلى الإشارة الرقمية.
المعلمات المهمة لـ WD:
- الحد الأقصى لمدى الجهد من الذروة إلى الذروة للإشارة الواردة
- دقة الشكل الموجي (دقة المحول الرقمي)
- العرض النطاقي
- عمق ذاكرة التقاط الشكل الموجي
- المقاومة الكهربائية للإدخال
- الضوضاء، الانحراف عن الموجة المثالية، نسبة الإشارة إلى الضوضاء، الاضافات
الساعة
تتم استقرار الساعات الرقمية والتناظرية من ساعة مرجعية عامة في النظام. في حالة عدم توفير إشارة تزامن للساعة، قد يؤدي التفاوت في التوقيت إلى النتائج غير الصحيحة.
معالج الإشارات الرقمية (DSP)
معالج الإشارات الرقمية (DSP) هو معالج دقيق متخصص يُقوم بأداء العمليات الرياضية على مجموعات من الأرقام الرقمية. يتم تنفيذ مختلف الخوارزميات مثل DFT وFFT على DSP لتحويل معلومات مجال الزمن إلى مجال التردد.
تم تصميم هندسة معالج DSP بطريقة محسنة لتمكين الضرب السريع، والجمع، وحسابات اللوغاريتم، والتربيع، وحسابات الجذر التربيعي.
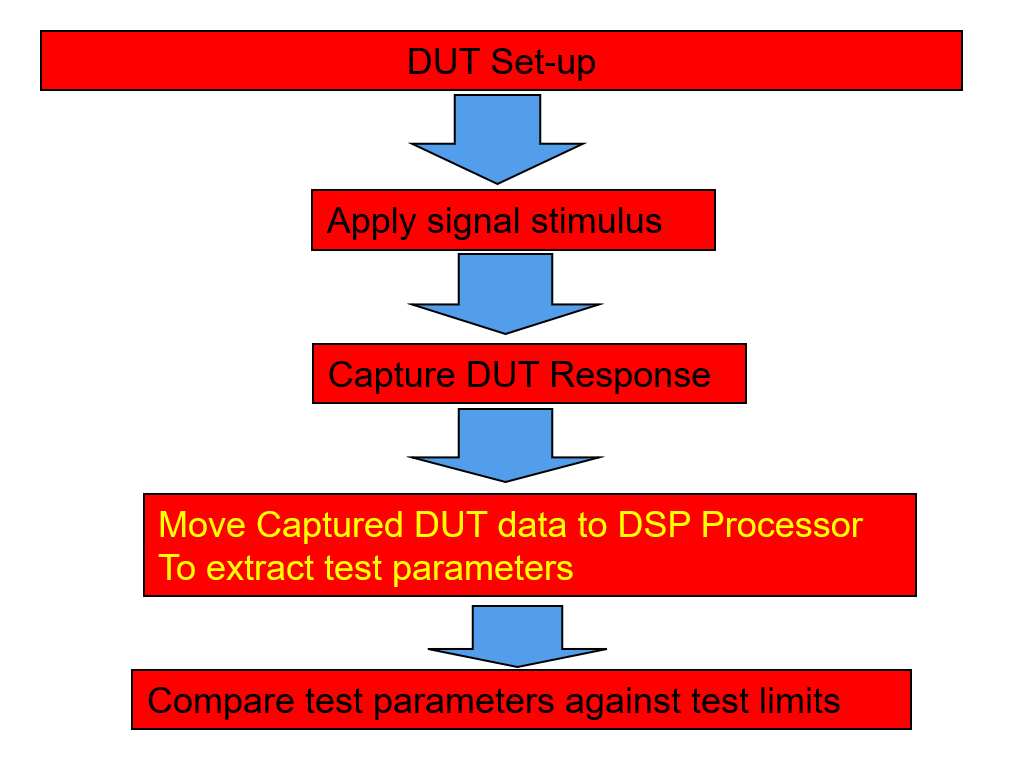
سيقوم الاختبار بنقل الإشارة المحتجزة المخزنة إلى معالج DSP من خلال حافلات البيانات.
المراجع والإشادات
- أساسيات الاختبار باستخدام ATE
- أساسيات الاختبار المختلط للإشارات_Brian-Lowe
المصدر: https://wiki-power.com/ هذا المنشور محمي باتفاقية CC BY-NC-SA 4.0، يجب إعادة الإنتاج مع الإسناد.
تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال. $$