RF - Resonant Circuit - Basic Definitions
In this major section, we will study parallel resonant circuits and their characteristics in RF, the concept of Q factor, and its relationship with source impedance and load impedance. We will also study the losses of components and how they affect the circuit, and finally, we will demonstrate some coupled resonant circuits.
Resonant circuits are used in RF circuits in every transmitter, receiver, and test equipment to selectively transmit a certain frequency or group of frequencies from the source to the load while attenuating all other frequencies outside the passband. An ideal resonant circuit looks like this:
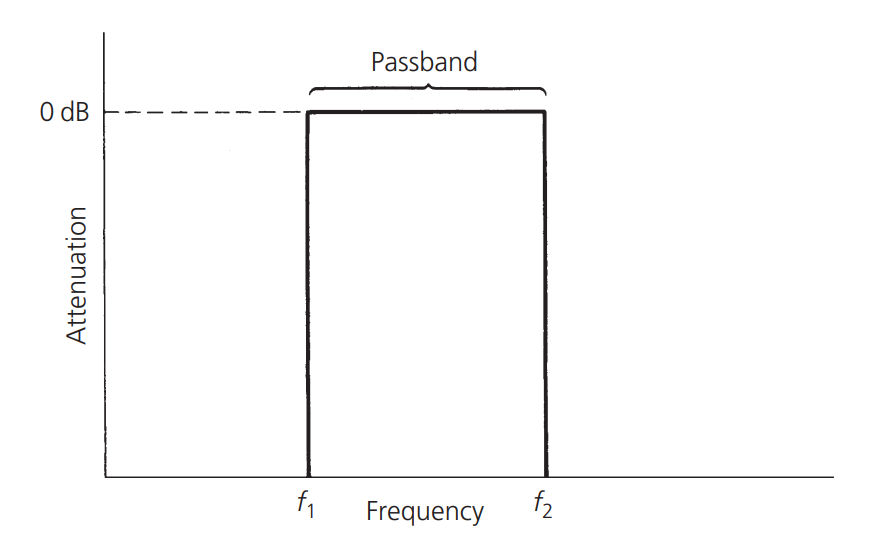
It is a perfect rectangular passband, attenuating wireless signals below or above the target bandwidth while allowing signals within the desired range to pass without interference. However, due to the physical properties of the components that make up the filter, a perfect filter is not possible, but we can design non-ideal filters that meet the requirements.
Bandwidth
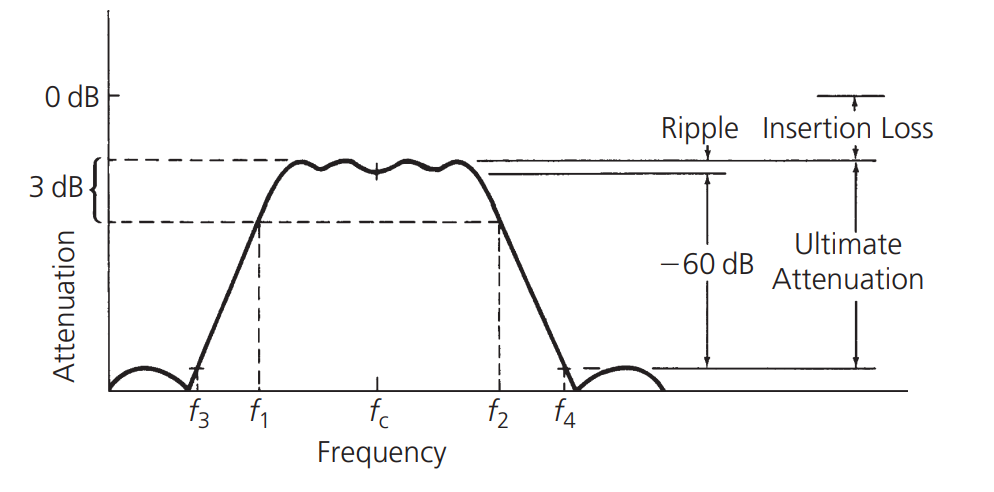
Bandwidth generally refers to the half-power bandwidth, which is the difference between the upper and lower frequencies where the amplitude response is 3dB lower than the passband response, as shown in the figure:
Meaning and Calculation of dB
dB is a relative value that can represent large or small numbers concisely. For example, if we want to represent a power change of 100,000,000 times, we only need to write +80dB.
Where \(P_1\) represents the current power and \(P_0\) represents the reference power. If \(P_1\) is twice \(P_0\), then:
If \(P_1\) is half of \(P_0\), then:
Similarly, +10dB represents a power increase of 10 times, and -10dB represents a power decrease to 1/10.
3dB often appears in power graphs or bit error rate graphs, where +3dB means doubling the power and -3dB means halving the power.
dBm and dBw
dBm and dBw are obtained by replacing the reference power \(P_0\) in the dB formula with 1 mW and 1 W, respectively:
Since 1 mW and 1 W are fixed values, dBm and dBw can both represent the absolute value of power.
There is a conversion table between current power and dBm, dBw:
| واط | ديسيبل مللي واط | ديسيبل واط |
|---|---|---|
| 0.1 بيكو واط | -100 ديسيبل مللي واط | -130 ديسيبل واط |
| 1 بيكو واط | -90 ديسيبل مللي واط | -120 ديسيبل واط |
| 10 بيكو واط | -80 ديسيبل مللي واط | -110 ديسيبل واط |
| 100 بيكو واط | -70 ديسيبل مللي واط | -100 ديسيبل واط |
| 1 نانو واط | -60 ديسيبل مللي واط | -90 ديسيبل واط |
| 10 نانو واط | -50 ديسيبل مللي واط | -80 ديسيبل واط |
| 100 نانو واط | -40 ديسيبل مللي واط | -70 ديسيبل واط |
| 1 ميكرو واط | -30 ديسيبل مللي واط | -60 ديسيبل واط |
| 10 ميكرو واط | -20 ديسيبل مللي واط | -50 ديسيبل واط |
| 100 ميكرو واط | -10 ديسيبل مللي واط | -40 ديسيبل واط |
| 794 ميكرو واط | -1 ديسيبل مللي واط | -31 ديسيبل واط |
| 1.000 مللي واط | 0 ديسيبل مللي واط | -30 ديسيبل واط |
| 1.259 مللي واط | 1 ديسيبل مللي واط | -29 ديسيبل واط |
| 10 مللي واط | 10 ديسيبل مللي واط | -20 ديسيبل واط |
| 100 مللي واط | 20 ديسيبل مللي واط | -10 ديسيبل واط |
| 1 واط | 30 ديسيبل مللي واط | 0 ديسيبل واط |
| 10 واط | 40 ديسيبل مللي واط | 10 ديسيبل واط |
| 100 واط | 50 ديسيبل مللي واط | 20 ديسيبل واط |
| 1 كيلو واط | 60 ديسيبل مللي واط | 30 ديسيبل واط |
| 10 كيلو واط | 70 ديسيبل مللي واط | 40 ديسيبل واط |
| 100 كيلو واط | 80 ديسيبل مللي واط | 50 ديسيبل واط |
| 1 ميجا واط | 90 ديسيبل مللي واط | 60 ديسيبل واط |
| 10 ميجا واط | 100 ديسيبل مللي واط | 70 ديسيبل واط |
من بينها، الأكثر استخدامًا هو 1 واط = 30 ديسيبل مللي واط.
dBi و dBd و dBc
طرق حساب dBi و dBd و dBc مشابهة لطريقة حساب dB، حيث تعبر عن قيمة القدرة النسبية، لكن معانيها تختلف بناءً على المعنى الذي يمثله المرجع \(P_0\).
| dBx | المرجع |
|---|---|
| dBi (ديسيبل إيزوتروبي) | هوائي ذو اتجاهية كروية (هوائي إيزوتروبي) |
| dBd (ديسيبل ديبول) | هوائي ذو اتجاهين (هوائي ديبول) |
| dBc (ديسيبل حامل) | حامل (حامل) |
عند تمثيل نفس الزيادة، يكون قيمة dBi عادة أكبر من dBd بمقدار 2.15، ويعود هذا الاختلاف إلى اتجاهيات مختلفة للهوائيين الاثنين.
نسبة تردد مركز الدائرة الموجية إلى عرض النطاق الترددي (Q)
هذا ال Q يختلف عن تعريف Q في المقالة السابقة. يعد Q قياسًا لانتقائية الدائرة الموجية، حيث يزداد قيمة Q، يصبح عرض النطاق الترددي أضيق، وتزداد انتقائية الدائرة الموجية. يتم تعريف Q بالمعادلة التالية:
عامل الشكل (SF)
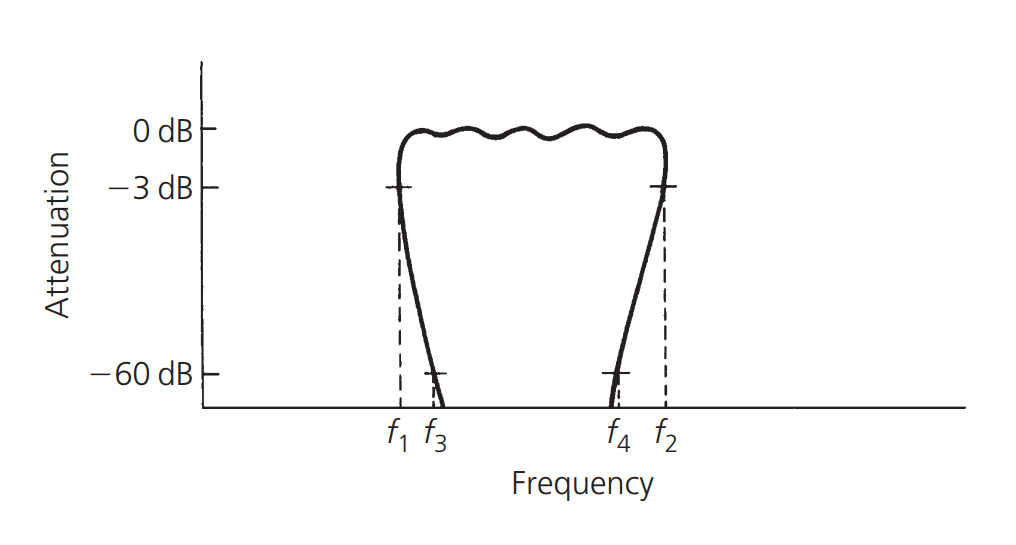
يتم تعريف عامل الشكل للدائرة الموجية عادة بنسبة عرض النطاق الترددي بمستوى 60 ديسيبل إلى عرض النطاق الترددي بمستوى 3 ديسيبل. على سبيل المثال، إذا كان عرض النطاق الترددي بمستوى 60 ديسيبل \(f_4 - f_3\) هو 3 ميغاهرتز، وعرض النطاق الترددي بمستوى 3 ديسيبل \(f_2-f_1\) هو 1.5 ميغاهرتز، فإن عامل الشكل يكون:
العامل الشكل هو طريقة لقياس حدة حافة الحافة. كلما كان الرقم أصغر ، زادت حدة حافة الحافة. عامل الشكل للمرشح المثالي هو 1 ، وهذا هو القيمة النهائية. النطاق الذي يكون عامل الشكل أقل من 1 كما هو موضح في الشكل التالي ، ولكن هذا غير ممكن في الواقع:
التخميد النهائي
يشير إلى الفرق بين النطاق الترددي وذروة التخميد الخارجية. بسبب الخصائص الفعلية للعناصر ، فإن التخميد النهائي لا يمكن أن يكون لانهائيًا.
فقدان الإدراج
يشير إلى فقدان التخميد الناجم عن المكونات بين مصدر الإشارة والنهاية. في حالة عدم تطابق الانتقالات ، يتم امتصاص بعض الإشارات من قبل هذه المكونات ، ويشار إلى هذا الفقدان بفقدان الإدراج ، ويتم تعبيره بوحدة ديسيبل.
التموج
يعبر التموج عن مستوى التسطح لنطاق المرشح المتوازن ، ويتم تعبيره بوحدة ديسيبل. يتم تعريف قيمته كفرق بين أقصى تخميد وأدنى تخميد في النطاق الترددي.
المراجع والشكر
- 《RF-Circuit-Design(second-edition)_Chris-Bowick》
- 100 分钟看懂 dB、dBm、dBw 的区别
عنوان النص: https://wiki-power.com/
يتم حماية هذا المقال بموجب اتفاقية CC BY-NC-SA 4.0، يُرجى ذكر المصدر عند إعادة النشر.تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال.