الأمواج اللاسلكية - أساسيات الهوائيات
هذا المقال سيقدم شرحاً لمبادئ الهوائيات والمعلمات الأساسية.
مبادئ الهوائيات
الهوائي (الأنتينا) هو جهاز يُستخدم لتحويل الإشارات الكهربائية على الأسلاك إلى إشارات إذاعية وإرسالها في الفضاء، ويمكن أيضاً استخدامه لاستقبال الإشارات الإذاعية في الفضاء وتحويلها إلى إشارات كهربائية (على العموم، هذه الطريقتين مبدئياً مماثلتين ولكن هناك استثناءات للهوائيات النشطة).
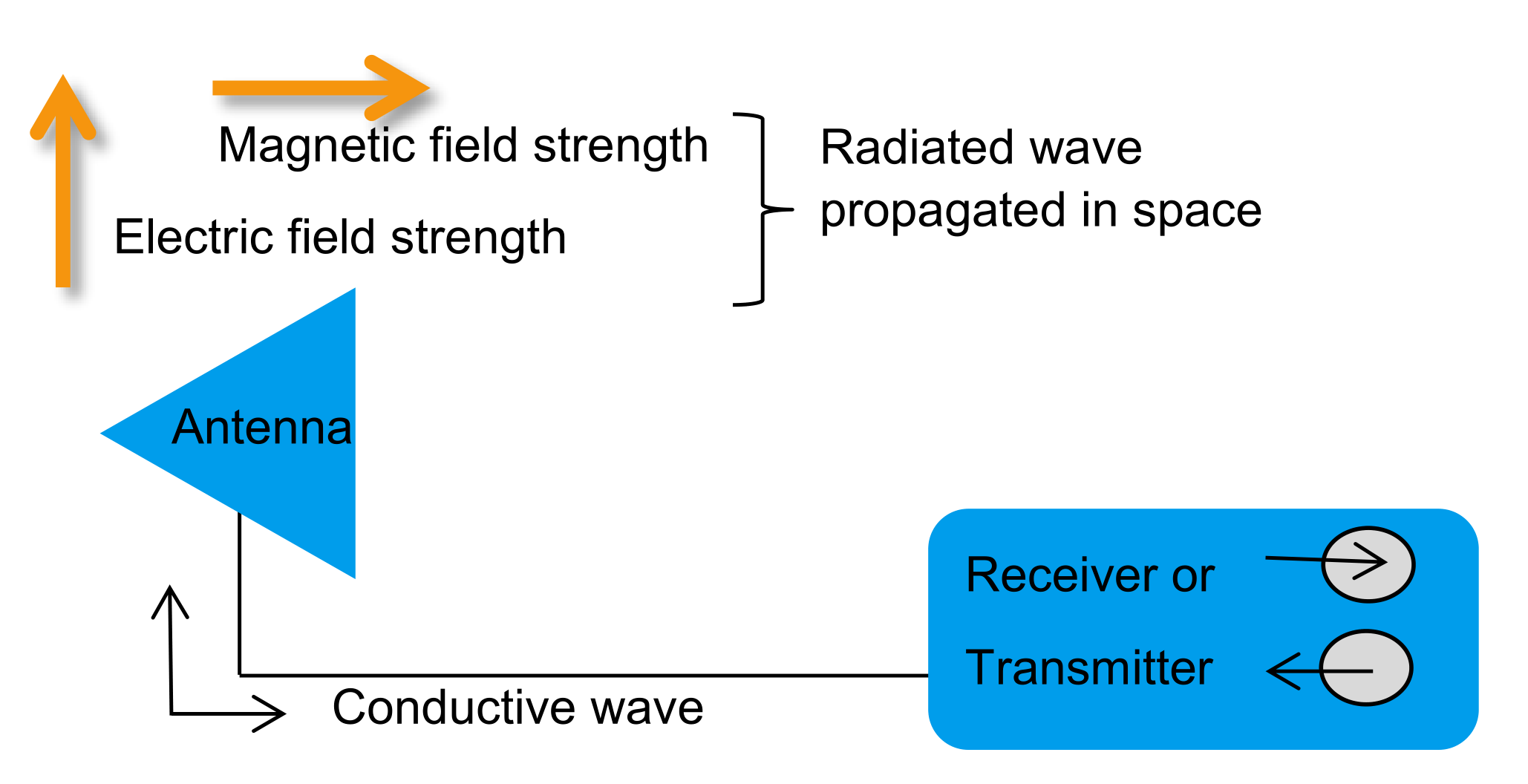
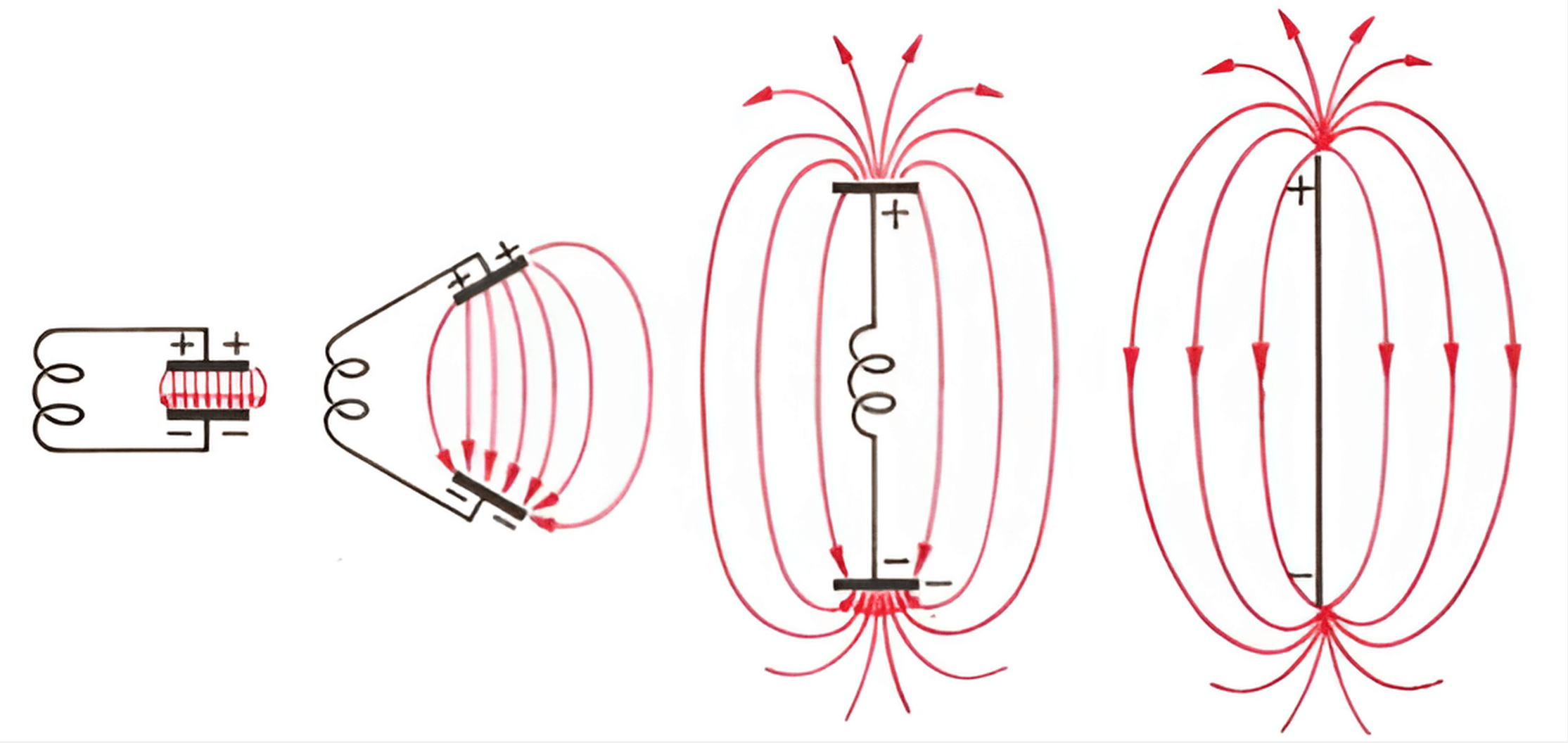
الهوائي ينشأ من مُذبذب يتألف من ملف ملفوف ومكثف موازي. عند تباعد اللوحين الموازيين، سيقل السعة بينهما. باعتبار هذا التباعد وسعة الملف نفسه على أنها سعة مُناسبة، ستكون هذه مذبذبة قطبية.
معلمات الهوائيات
كثافة الإشعاع (Radiation Density)
لنفترض وجود جهاز إرسال ميكروويف مثالي ومتجانس من الناحية الاتجاهية، يشكل نقطة في الفضاء وينتج موجة كروية واجتاحت الفضاء بتساوي في جميع الاتجاهات.
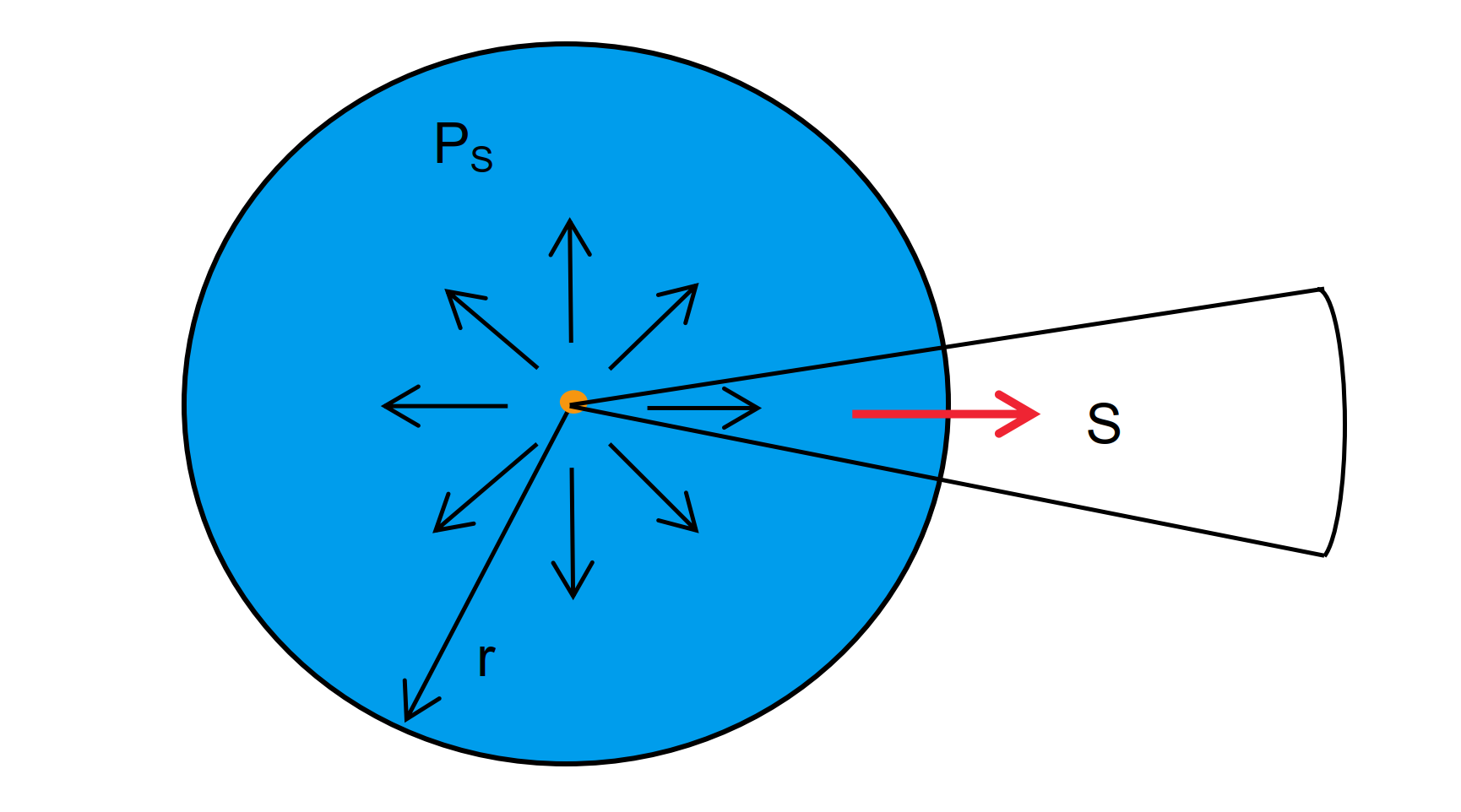
عند تطبيق قدرة الإرسال \(P_S\) على هذا الجهاز في مسافة \(r\)، يمكن حساب كثافة الإشعاع (أو كثافة الطاقة) على النحو التالي:
يمكن أيضا تعريف كثافة الإشعاع عن طريق حاصل ضرب الحقل الكهربائي والحقل المغناطيسي في الفضاء البعيد:
نمط الإشعاع (Radiation Pattern)
نمط الإشعاع يُستخدم لوصف تأثير الإشعاع الثلاثي الأبعاد في الفضاء عند الهوائي. بالنسبة لمُولد الإشعاع متجانس في جميع الاتجاهات (الذي نشير إليه فيما بعد باسم الهوائي نقطي)، فإن حجم الإشعاع متساوي في كل اتجاه، لكنه لا يمكنه التحليل في اتجاه معين. بالنسبة للهوائيات العامة مثل هوائي الزوج القصير وهوائي الموجة الأحادية، يكون لديها اتجاه.
على سبيل المثال، يمكن رؤية نمط الإشعاع الثلاثي الأبعاد لهوائي الزوج القصير في الفضاء الحر كما هو موضح في الصورة أدناه. يمكن ملاحظة أنه لا يوجد كثافة إشعاع في اتجاه محور الهوائي:
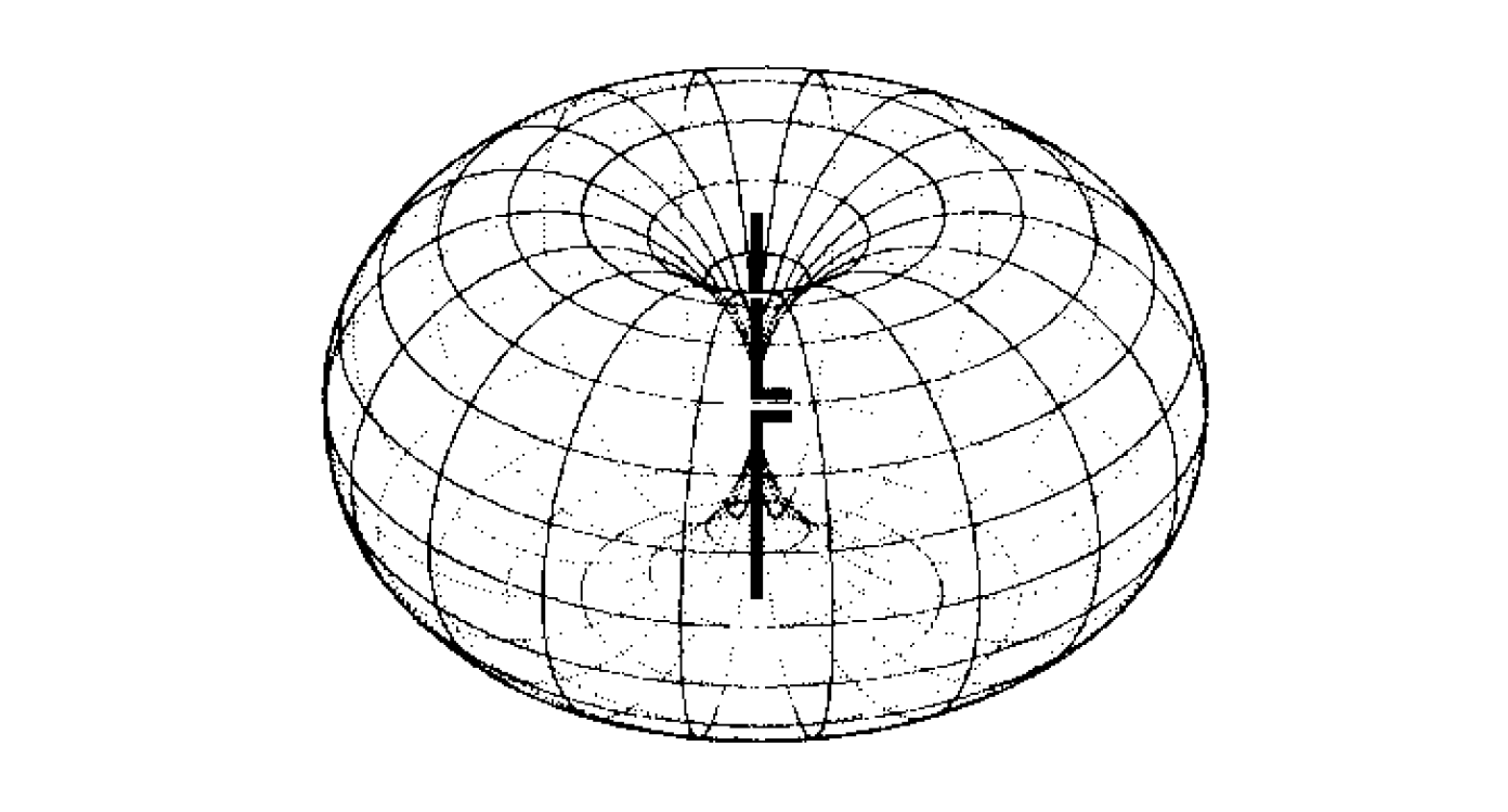
بالإضافة إلى عرض الإشعاع الثلاثي الأبعاد، يتم تمثيل الإشعاع أيضاً بواسطة رسومات القطع الثنائي البعدي (نمط الإشعاع الرئيسي) على المستويين الأفقي والرأسي كما هو موضح في الصورة أدناه:
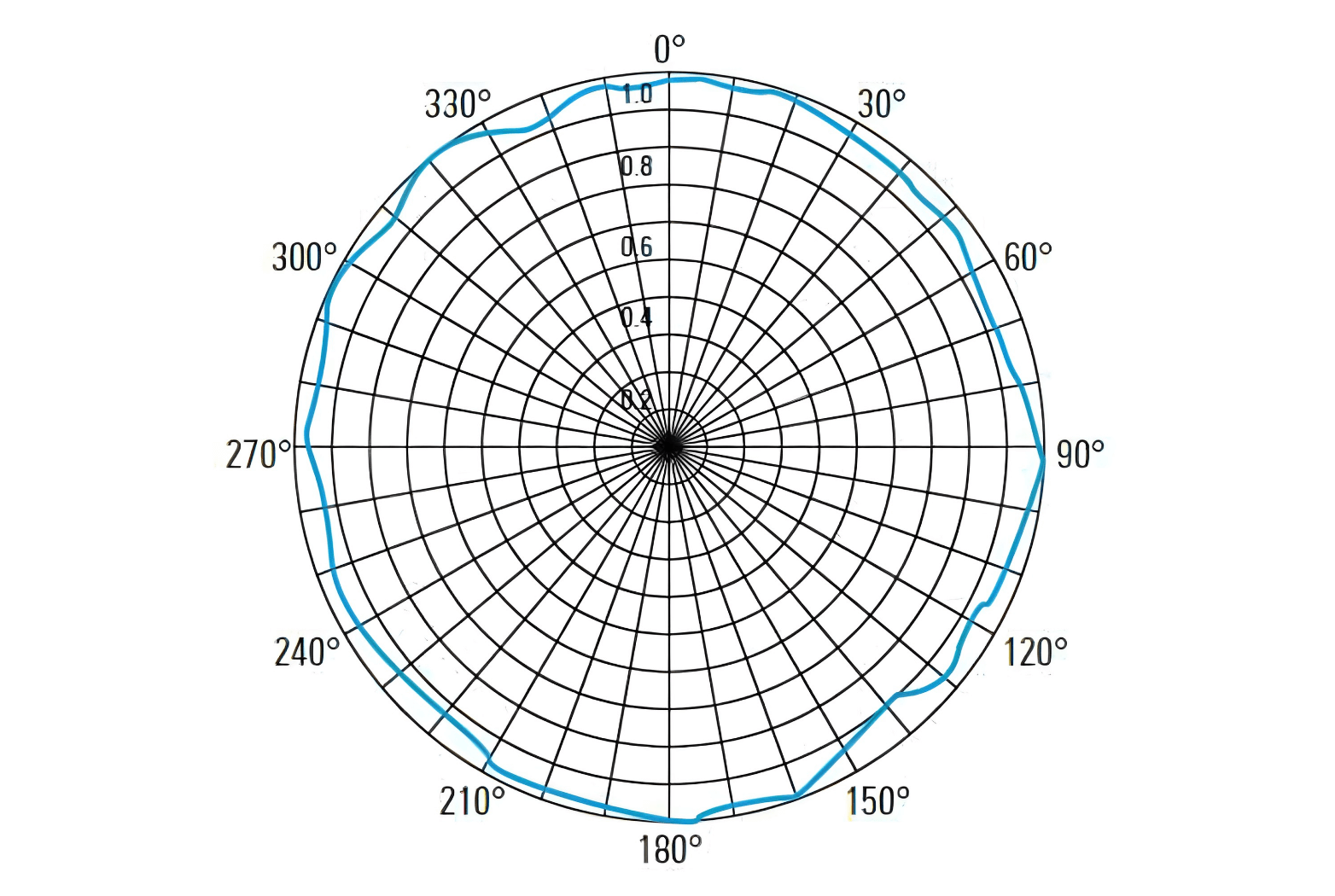
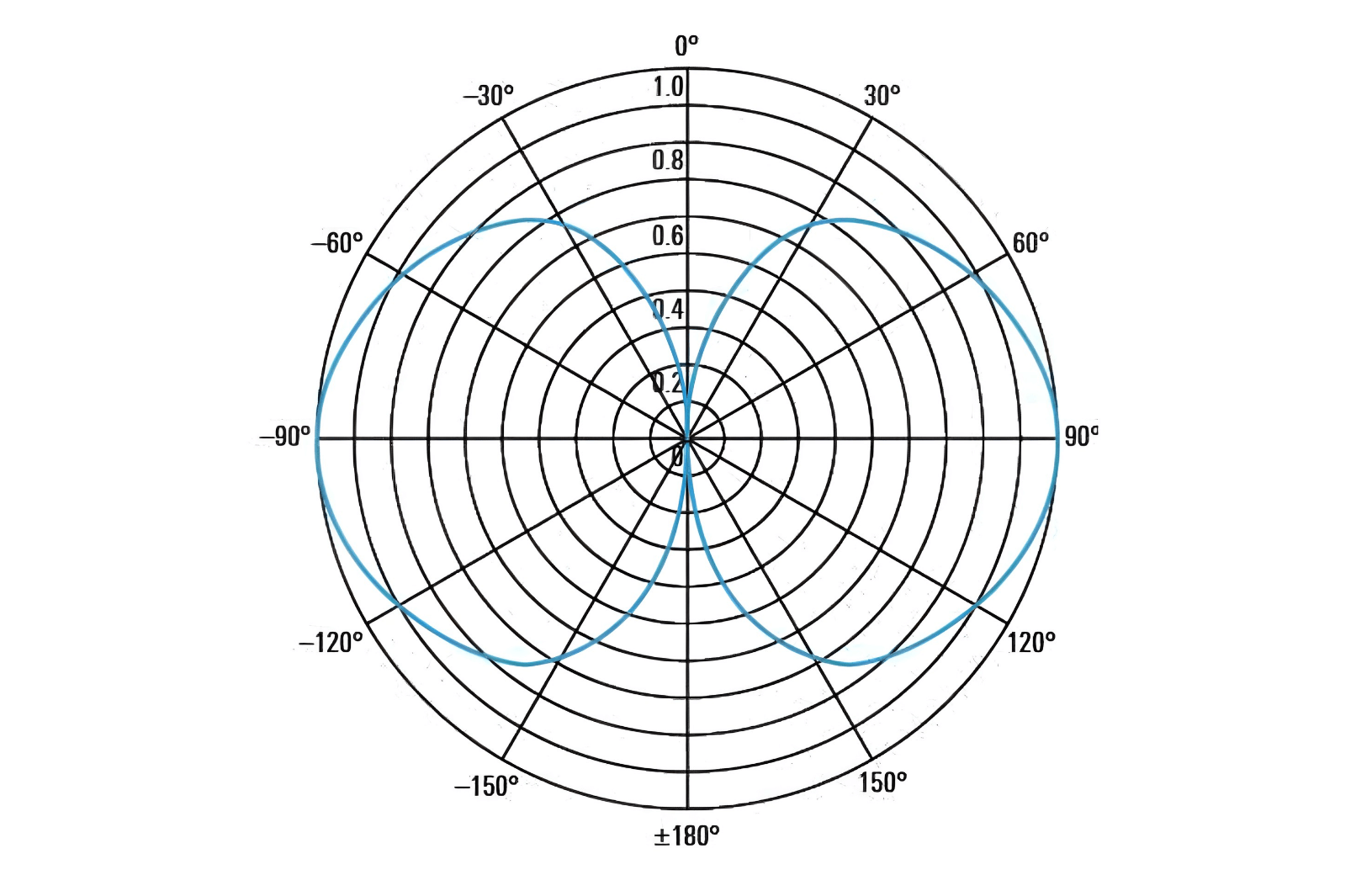
عادة، يتم رسم نمط الإشعاع في نظام إحداثيات قطبي حتى يمكن معرفة كثافة الإشعاع في كل اتجاه. في بعض الحالات (مثل الهوائيات عالية الاتجاهية)، يمكن تمثيل نمط الإشعاع في نظام إحداثيات كارت
**ملاحظة:** في الميدان البعيد، $\vec S$ يكون عموديًا على $\vec E$، و $\vec S$ و $\vec E$ يكونان عموديين على $\vec H$.
الكثافة الطاقية تُقاس عند المسافة نفسها $r$ من الهوائي، لذلك عندما $F_i = \frac{P_t}{4\pi}$ ، يمكن الحصول على:
$$
D=\frac{F_{max}}{F_i}
$$
### الكفاءة (Efficiency)
عادةً ما يُعرف كفاءة الهوائي $\eta$ بوصفها نسبة القدرة الإشعاعية للهوائي إلى القدرة الداخلة. يمكن للهوائي ذو الكفاءة العالية إشعاع معظم الطاقة المُدخلة، بينما يتم امتصاص معظم الطاقة في الهوائي ذو الكفاءة المنخفضة كخسائر داخل الهوائي أو نتيجة عدم تطابق المعاوقة. بالنسبة للهوائيات الغير نشطة، سواء كانت هوائيات إرسال أو استقبال، فإن الكفاءة متساوية دائمًا، وهذه الخاصية تُعرف بالتبادل الهوائي (Antenna Reciprocity). صيغة كفاءة الإشعاع للهوائي $\varepsilon_R$ كما يلي:
$$
\varepsilon_R=\frac{P_{refl}}{P_{forw}}\cdot 100\%
$$
ليس فقط تُعبّر الكفاءة عن النسبة المئوية، ولكنها غالبًا ما تُعبّر بالديسيبل. على سبيل المثال، كفاءة 10% تعادل -10 ديسيبل، وكفاءة 50% تعادل -3 ديسيبل.
الصيغ المذكورة أعلاه تُمثل كفاءة الإشعاع للهوائي، وهناك أيضًا نوع آخر من الكفاءة يُعرف بكفاءة الهوائي الإجمالية $\varepsilon_r$. العلاقة بينهما هي أن الكفاءة الإجمالية تساوي كفاءة الإشعاع مضروبة في خسائر تطابق المعاوقة $M_L$:
$$
\varepsilon_r=M_L\cdot\varepsilon_R
نظرًا لأن خسائر تطابق المعاوقة تتراوح بين 0 و 1، فإن الكفاءة الإجمالية للهوائي ستكون دائمًا أقل من الكفاءة الإشعاعية. إذا تطابقت المعاوقة بشكل كامل، ستكون الكفاءتين متساويتين. في الواقع، عادةً ما يشير الحديث عن كفاءة الهوائي إلى الكفاءة الإجمالية بعد مراعاة خسائر تطابق المعاوقة بالأخص، ولذا، يمكن تحسين الكفاءة الفعلية للهوائي بمطابقة المعاوقة بشكل أفضل.
الربح (Gain)
يُستخدم الربح الهوائي لقياس قدرة الهوائي على إرسال أو استقبال إشارات في اتجاه معين. الربح يتعلق ارتباطًا بالرسم الاتجاهي للهوائي، حيث تزيد الرسوم الرئيسية الضيقة والفروع الجانبية الصغيرة عندما يكون الربح عاليًا.
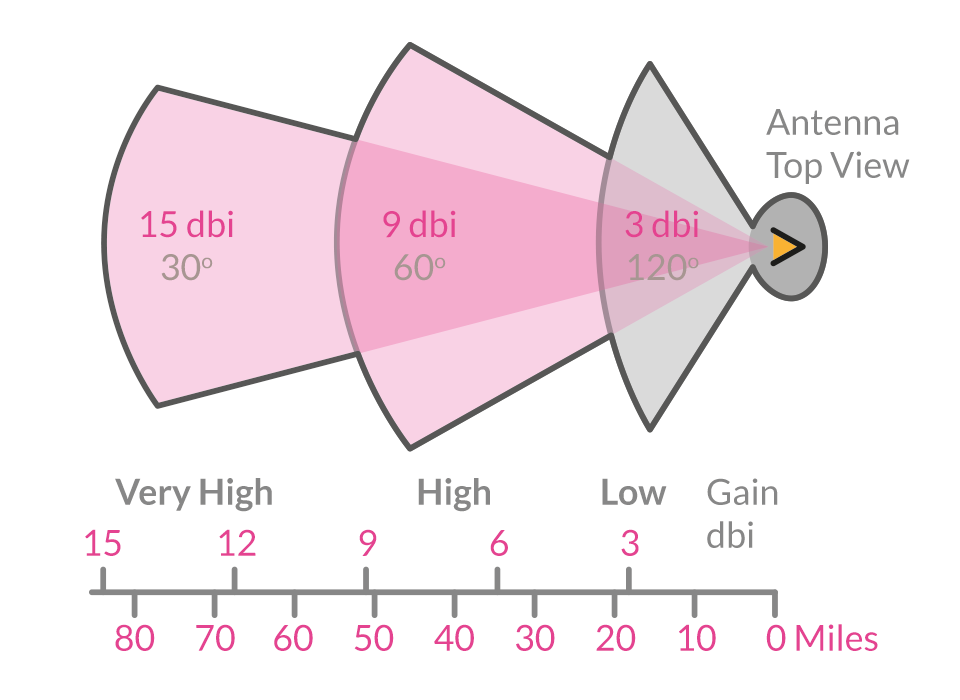
في نفس الظروف، كلما زاد الربح، ازداد تركيز الطاقة، وازدادت مدى انتقال الموجة الكهرومغناطيسية، ولكن زاوية الاستغطاء تصبح أضيق. لذلك، يجب اختيار الربح الهوائي بعناية في التطبيقات العملية.
الربح الهوائي يتوافق مع معامل الاتجاه، ويُظهر كنسبة بين الكثافة الإشعاعية القصوى $F_{max}$ والكثافة الإشعاعية التي يُنتجها الهوائي نفسه بنفس الطاقة ( $P_{t0}$ ) بدون خسائر. عندما $F_{i0}=\frac{P_t}{4\pi}$
I have translated the text into Arabic while maintaining the original markdown format:
$$
A_W=A_g\cdot q
$$
مساحة الهوائي الفعّالة مرتبطة أيضًا بالمكاسب (يمكن أن تتبادل بينهما):
$$
A_W=\frac{\lambda ^2}{4\pi}\cdot G
$$
### المقاومة الداخلية (Input Impedance)
المقاومة الداخلية للهوائي هي معلمة حاسمة، إنها قيمة معقدة تتألف من المقاومة الحقيقية والمقاومة التفاعلية:
$$
Z_{in}=R_{in}+jX_{in}
$$
حيث المقاومة الحقيقية $R_{in$ تتألف من مقاومة الإشعاع $R_R$ ومقاومة الخسارة $R_L$:
$$
R_{in}=R_R+R_L
$$
بالنسبة للهوائيات الصغيرة، يتعين تحديد موقع مقاومة الإشعاع $R_R$ على الهوائي لحسابها، لأنها مرتبطة بالمكان (حيث يتناسب قوة الإشعاع مع متوسط جذر مربع التيار الكهربائي للهوائي). وبالنسبة للتيار الكهربائي في الهوائي، يجب أيضًا تحديد نقطة تغذية الهوائي للحصول على أعلى قيمة تيار كهربائي.
إذا كان الهوائي يعمل في حالة التردد المنسجم (التردد المنسجم)، فإن المكون التفاعلي للمقاومة الداخلية يكون صفرًا. الهوائيات الخطية قصيرة عادة تظهر سعة (X_{in}<0$)، بينما الهوائيات الخطية الطويلة تظهر عادة ملامسة ($X_{in}>0$).
### المقاومة الاسمية (Nominal Impedance)
المقاومة الاسمية $Z_n$ عادة ما تكون قيمة مقاومة الخط للاتصال بالهوائي وتكون عادة مساوية لـ 50 أوم. عادة ما يجب أن تتطابق مقاومة الهوائي مع هذه القيمة.
### تطابق المقاومة (Impedance Matching)
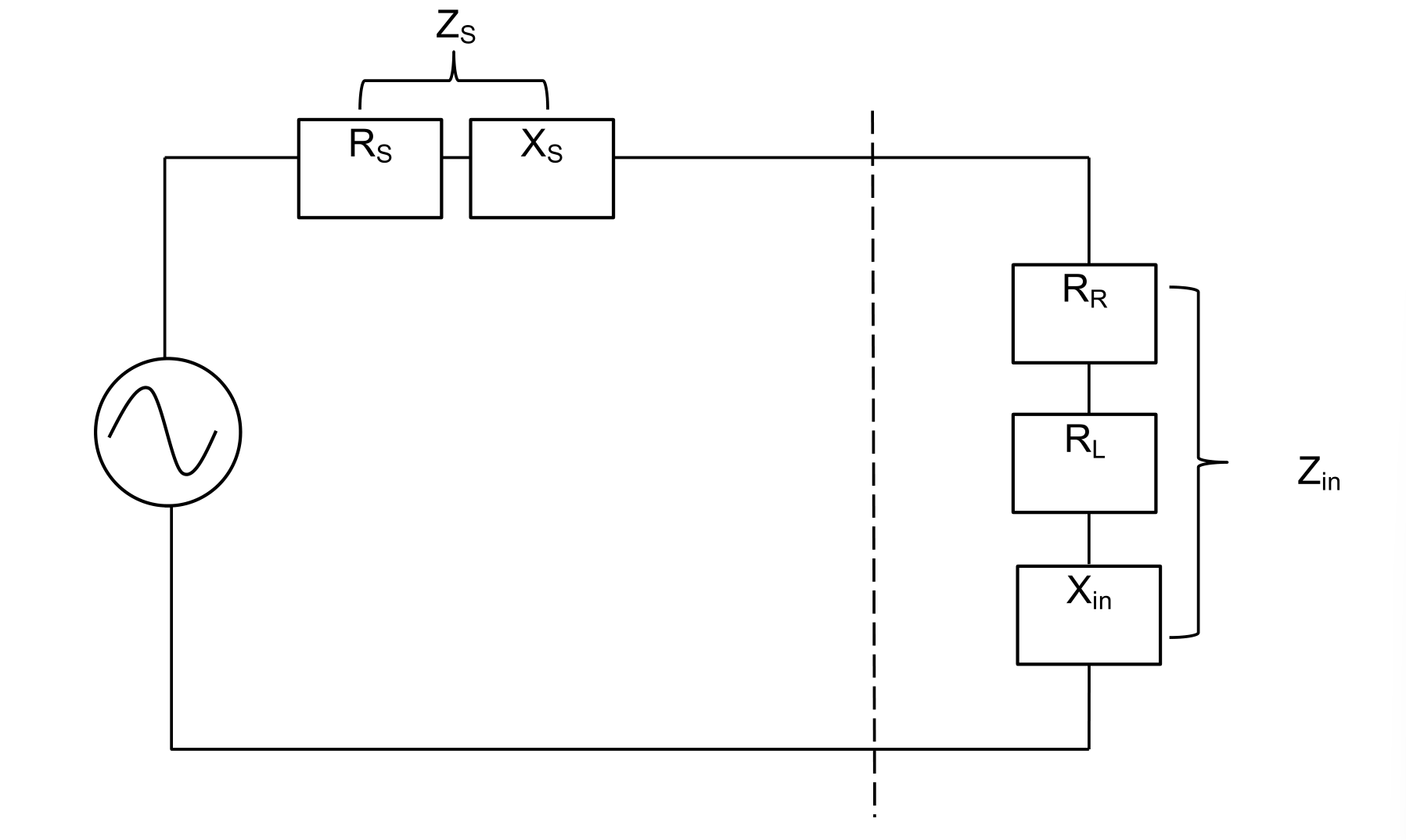
إذا كانت مقاومة الهوائي والخط ونهاية المصدر غير متطابقة، فستحدث عدم استمرارية. على سبيل المثال، في الرسم أدناه، جزء من الطاقة المرسلة من نهاية المصدر تنعكس ولا تصل إلى الهوائي، مما يؤثر على أداء الإرسال. وبالمثل، لا يمكن نقل جميع الطاقة المستلمة من الهوائي إلى جهاز الاستقبال:
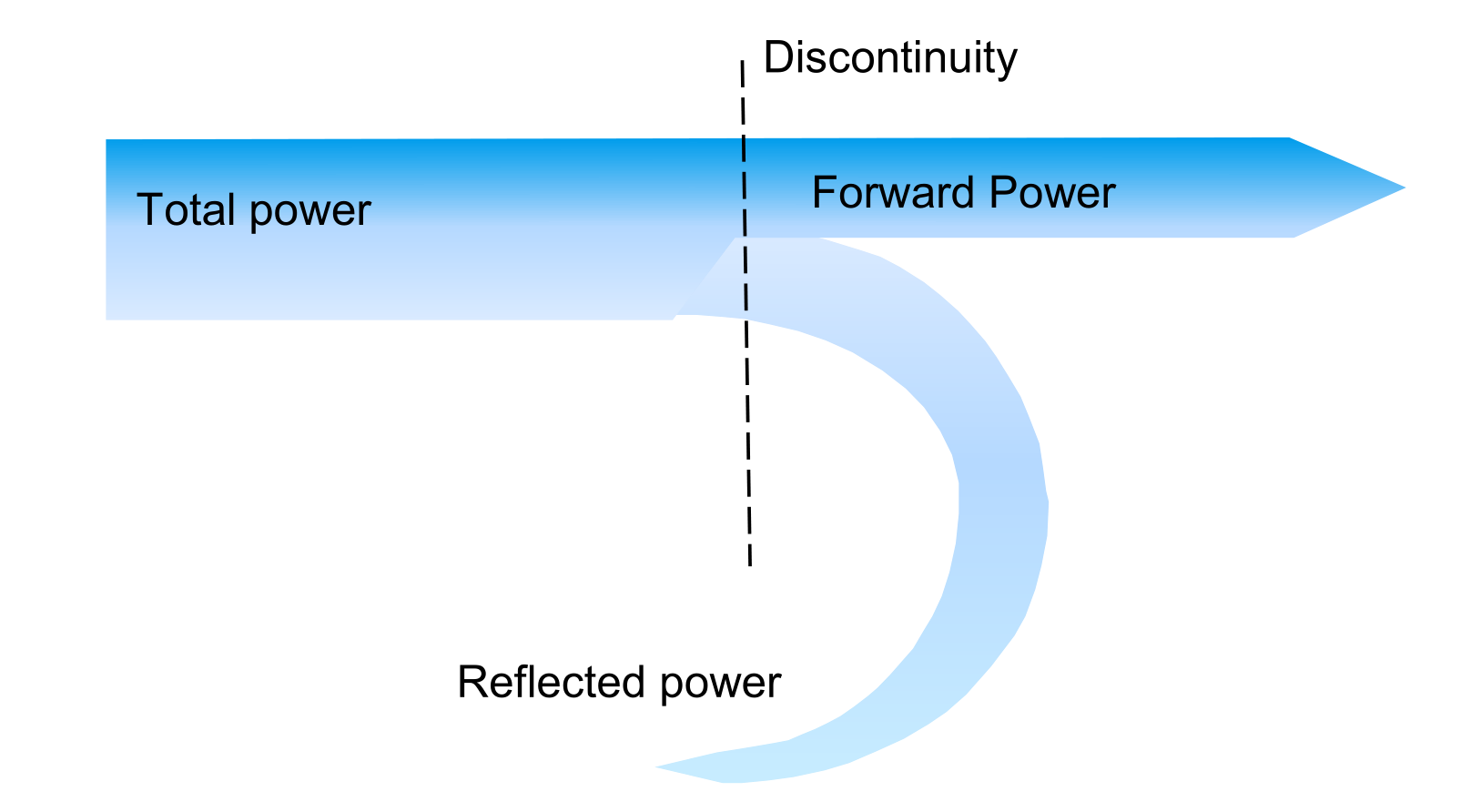
يمكن رؤية تطابق المقاومة من خلال الدائرة الكهربائية الكاملة للهوائي. يتعين تحقيق $Z_S=Z_{in}$ للحصول على أقصى قدرة نقل:
### نسبة الموجة الواقفة (Voltage Standing Wave Ratio, VSWR)
إذا كانت المقاومة غير متطابقة، قد تتسبب في عودة بعض الطاقة وتوليد موجات واقفة. نستخدم نسبة الموجة الواقفة $s$ لوصف خصائص الموجات الواقفة، والتي تعرف كنسبة بين أقصى وأدنى جهد على الخط (أو يمكن حسابها بناءً على نسبة التيار):
$$
s=\frac{V_{max}}{V_{min}}=\frac{I_{max}}{I_{min}}
$$
بالإضافة إلى ذلك، يمكن أيضًا حساب نسبة الموجة الواقفة باستخدام القيم القمة للجهد الواقف والجهد المنعكس:
$$
s=\frac{|V_{forw}|+|V_{refl}|}{|V_{forw}|-|V_{refl}|}=\frac{\sqrt{P_{forw}}+\sqrt{P_{forw}}}{\sqrt{P_{forw}}-\sqrt{P_{forw}}
$$
نسبة الجهد المنعكس $V_{vref}$ إلى الجهد المرسل $V_{forw}$ تعرف باسم معامل الانعكاس $r$ (Reflection Coefficient):
$$
```markdown
| VSWR | R | $a_r$ | الطاقة المنعكسة |
| ----- | ----- | ----- | ---------------- |
| 1.002 | 0.001 | 60 ديسيبل | \ |
| 1.01 | 0.005 | 46 ديسيبل | \ |
| 1.1 | 0.05 | 26 ديسيبل | 0.2% |
| 1.2 | 0.1 | 20 ديسيبل | 0.8% |
| 1.5 | 0.2 | 14 ديسيبل | 4% |
| 2.0 | 0.33 | 9.5 ديسيبل | 11.1% |
| 2.0 | 0.5 | 6 ديسيبل | 25% |
| 5.0 | 0.67 | 3.5 ديسيبل | 44.4% |
### العامل الهوائي (عامل الهوائي)
العامل الهوائي (أيضًا يُسمى عامل الهوائي أو معامل التحويل) هو عبارة عن قيمة تستخدم عادة مع الهوائات الاستقبالية. يتم تعريفه على أنه النسبة بين الحقل الكهربائي والجهد الكهربائي الناتج المقاس عند نقطة التغذية (تحت 50 أوم). يمكن تعبير عنه عادة بشكل لوغاريتمي كالتالي:
$$
K = \frac{E}{V}
$$
في معظم الأحيان، يُعبّر أيضًا عنه بشكل لوغاريتمي كـ dBm:
$$
k = 20 \log K
$$
إذا تم معايرة الهوائة في المصنع، عادة ما تكون قيمة العامل الهوائي ثابتة. والعلاقة بين العامل الهوائي والزيادة الفعلية كما يلي:
$$
K = \frac{9.73}{\lambda \cdot \sqrt{G}}
$$
$$
k = -29 ديسيبل + 20 \log \left(\frac{f}{ميجاهرتز}\right) - g
$$
### النطاق الترددي (النطاق الترددي)
يُستخدم معامل النطاق الترددي لقياس نطاق التردد الذي يمكن للهوائة استخدامه بكفاءة. خلال هذا النطاق، يمكن للهوائة أن تلبي متطلبات الأداء. وعادةً ما تكون معايير النطاق الترددي هي التطابق في الانعكاس (VSWR < 1.5)، والزيادة، وقمع الجوانب الثانوي وغيرها من المعاملات.
بالنسبة للهوائات عريضة النطاق، يتم تحديد نسبة النطاق بين أعلى وأدنى تردد يمكن استخدامه. على سبيل المثال، نسبة 2:1 تسمى ضعف التردد، ونسبة 10:1 تسمى عشرة أضعاف التردد:
$$
BW = \frac{f_H}{f_L}
$$
الهوائات العريضة النطاق تشير إلى BW ≥ 2. هناك أيضًا تعريف آخر للنطاق الترددي ينطبق فقط على الهوائات ذات النطاق الضيق:
$$
BW = \frac{f_H - f_L}{f_C} \cdot 100\%
$$
حيث يُمثل $f_C$ التردد المتوسط. قد يتجاوز قيمة هذا النطاق الترددي 100% (≤200%).
## المراجع والشكر
- "Antenna-Basics_Rohde&Schwarz"
- "كيفية اختيار الهوائة في نظام الموجات الكهرومغناطيسية_Rohde&Schwarz"
- [زيادة الهوائة | دليل سريع لهوائات WLAN](https://support.huawei.com/enterprise/zh/doc/EDOC1000062973/cb29154d)
- [ما هو معامل الزيادة للهوائة](https://www.netxl.com/blog/networking/antenna-gain/)
> عنوان النص: <https://wiki-power.com/>
> يتم حماية هذا المقال بموجب اتفاقية [CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by/4.0/deed.zh)، يُرجى ذكر المصدر عند إعادة النشر.
تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال.