射频 - 谐振电路 - 负载 Q 值 🚧
我们将谐振电路的中心频率与其 3dB 衰减带宽之比定义为谐振电路的 Q 值,也称为负载 Q 值,因为它描述了实际电路内或负载条件下谐振电路的通带特性。谐振电路的负载 Q 取决于三个主要因素:
- 源阻抗 \(R_s\)
- 负载电阻 \(R_L\)
- 上一章提到的元器件的 Q 值
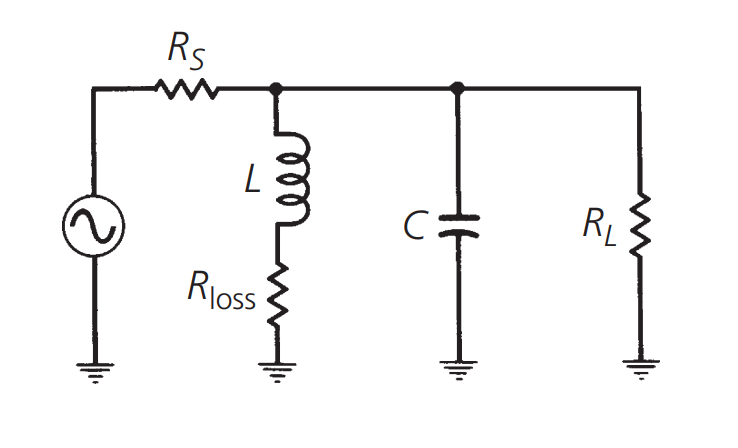
\(R_s\) 和 \(R_L\) 对负载 Q 的影响
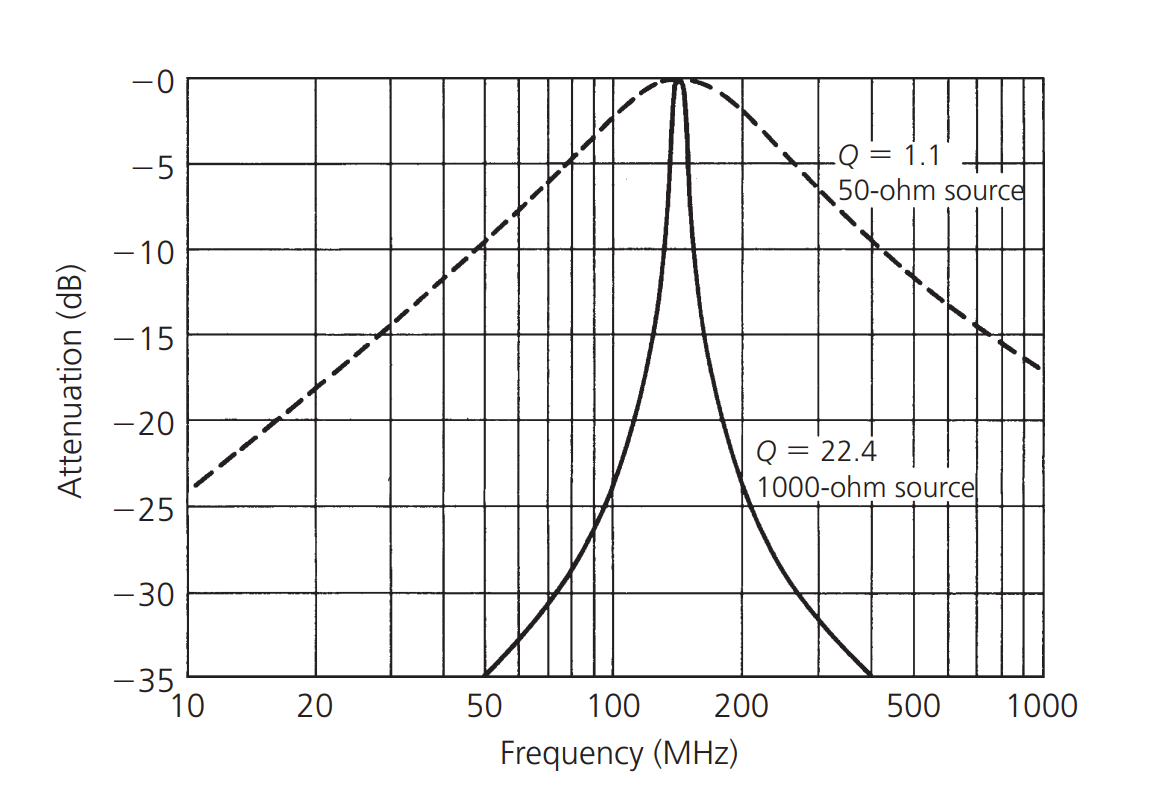
源阻抗和负载阻抗对谐振电路的负载 Q 的影响如上图所示。原始曲线(虚线)是由 50Ω 源阻抗,0.05uH 的无损电感器和 25pF 无损电容器组成的电路的谐振曲线,它的 Q 值由上文的公式 \(Q=\frac{f_e}{f_2-f_1}\) 计算约为 1.1,显然这不是一个非常窄带或高 Q 值的设计。
把源阻抗变为 1000Ω,绘制出一条新的谐振曲线(实线),谐振电路的 Q 值明显增加到 22.4。通过提高源阻抗,我们增加了谐振电路的 Q 值。
上面的方法并不能看出负载阻抗对谐振曲线的影响。如果像这样把外部负载连接到谐振电路:
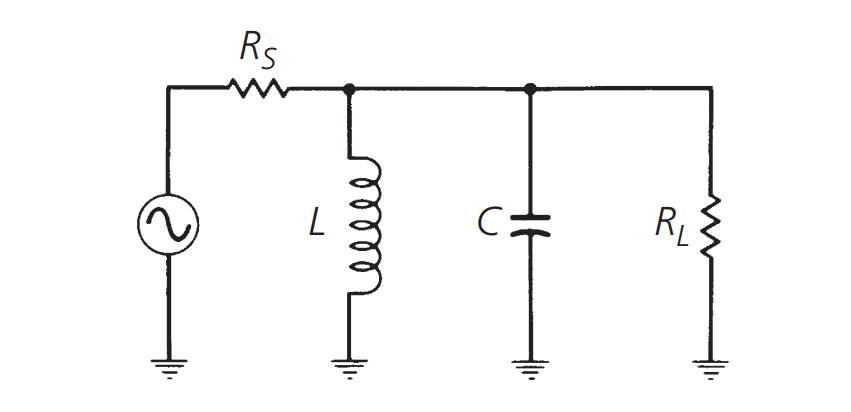
可以等效为:
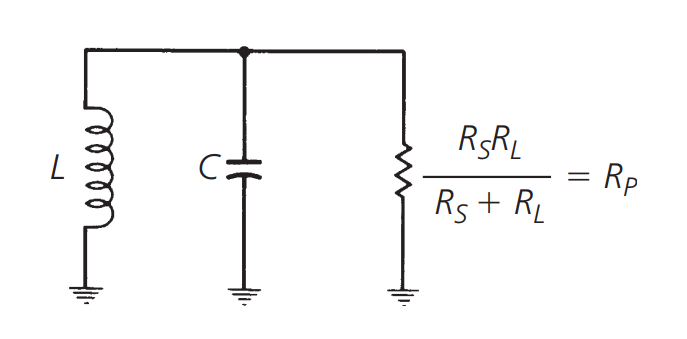
此时负载 Q 可以表示为:
其中,\(R_p\) 是等效总并联电阻,\(X_p\) 表示容抗 / 感抗(他们在谐振时是相等的)。
e.g. 如果我们要设计一个谐振电路,使其在 150Ω 的源阻抗和 1000Ω 的负载阻抗条件下运行。在 50 MHz 的谐振频率下,负载 Q 须等于 20。假设无损耗元件且无阻抗匹配。那么我们可以得出 \(R_p=130Ω\),根据上文公式,\(X_p=\frac{R_p}{Q}=\frac{130}{20} =6.5Ω\),又因为 \(X_p=\omega L=\frac{1}{\omega C}\),因此,可选 20.7nH 的电感、489.7pF 的电容。
可以看出,\(R_p\) 的降低会降低谐振电路的 Q 值,并且,如果 \(R_p\) 不变、改变 \(X_p\),可以获得相同的效果。因此,对于给定的源阻抗和负载阻抗,当电感为小值而电容器为大值时,可以获得谐振电路的最佳 Q 值。无论哪种情况,\(X_p\) 都会降低。例如:
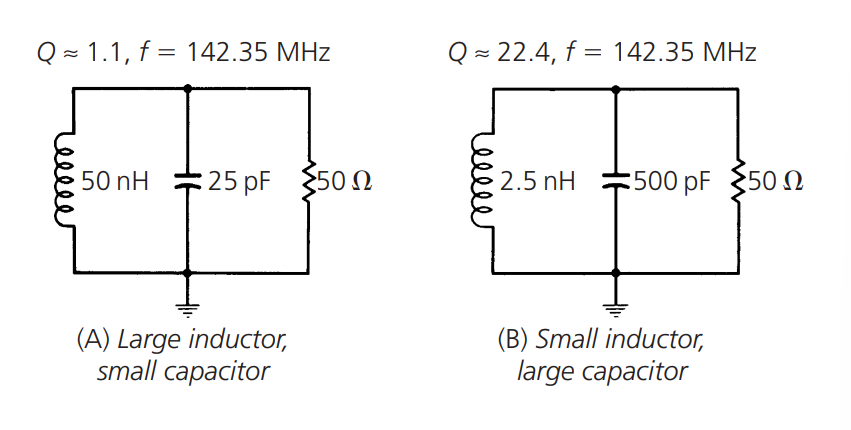
因此,采用这两种方法都可以对 Q 值进行调整:
- 选择源阻抗和负载阻抗的最佳值。
- 选择优化 Q 的 L 和 C 的分量值。
但通常我们只能用第二种方法,因为在许多情况下,源和负载是定好的,没法去改变他们。这种情况下,\(X_p\) 受一个给定的 Q 值定义,但通常算出来的值没有合适的实物值与之匹配,在下文将给出解决方法。
元器件的 Q 值对负载 Q 值的影响
在上文中,我们都是假设谐振电路中使用的元件是无损器件,元器件的 Q 值不会对负载 Q 值产生影响。但在非理想情况下,我们必须考虑单个元件的 Q 值。
在无损谐振电路中,谐振时电路端子上的阻抗是无限大的。但在实际电路中,由于元件损耗,会存在一些等效并联电阻:
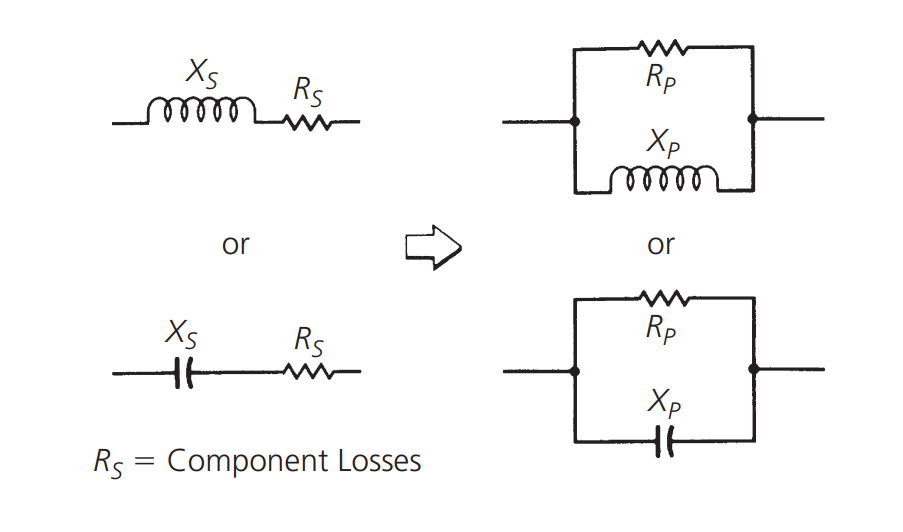
电阻 (Rp) 及其相关的并联电抗 (Xp) 可以从
参考与致谢
- 《RF-Circuit-Design(second-edition)_Chris-Bowick》
原文地址:https://wiki-power.com/
本篇文章受 CC BY-NC-SA 4.0 协议保护,转载请注明出处。