跳转至

太阳高度角计算

表示太阳在天空中的位置，首先需要选定坐标系，通常用到的坐标系有两种，一种是赤道坐标系，一种是地平坐标系。

概念：

  • 纬度 \(\varphi\)：-90°~90°，北纬为正。

赤道坐标系

赤道坐标系以赤道面为基本平面，以 赤纬角 和 时角 两个量来定义太阳的位置。

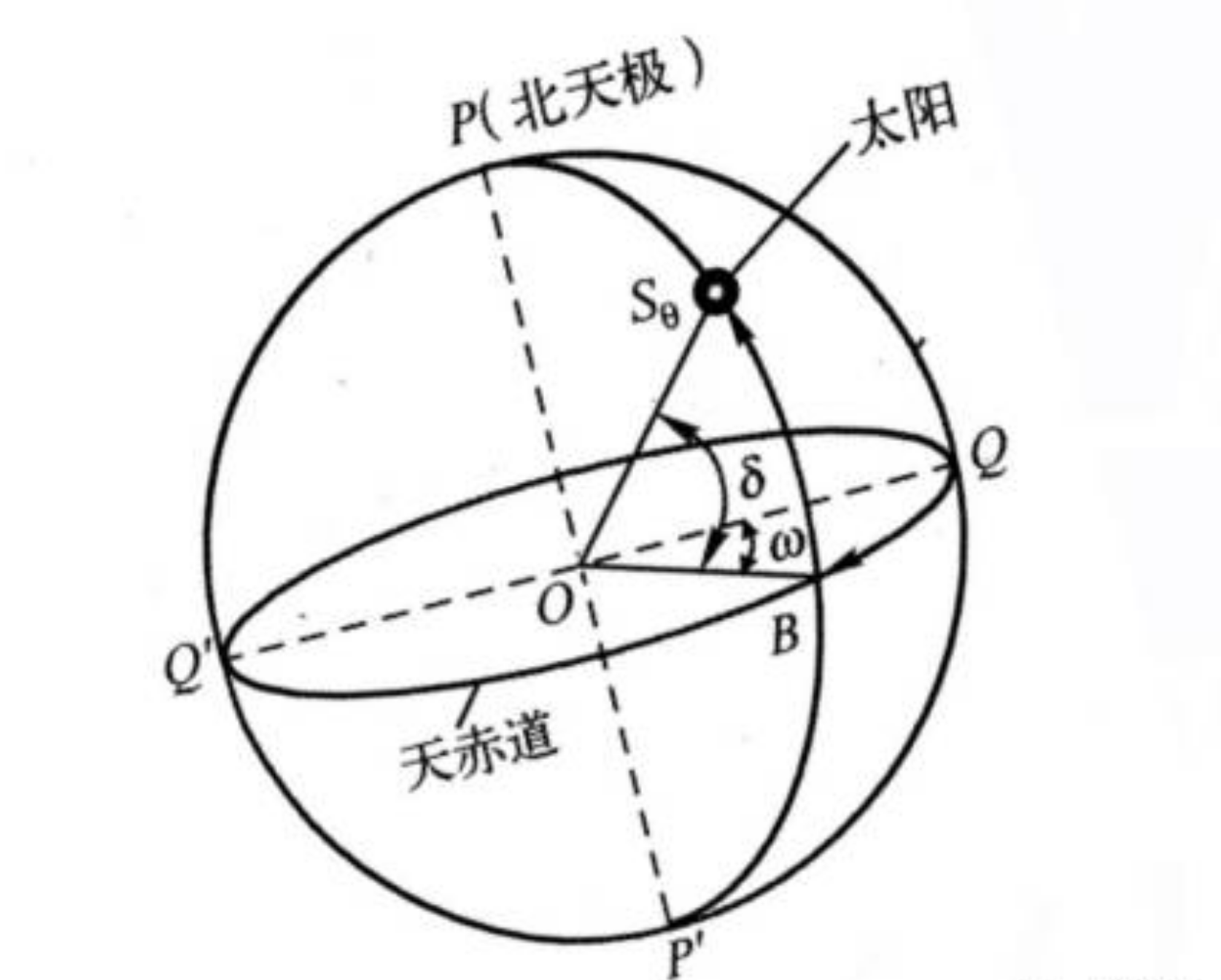
  • 赤纬角 \(\delta\) ：地日连线与赤道面的夹角
  • 时角 \(\omega\)：上午为负，下午为正，在数值上等于离正午时间（单位是 h）乘以 15°。

赤纬角会随着公转轨道的位置，在北回归线到南回归线之间（-23.45°~23.45°）变化：

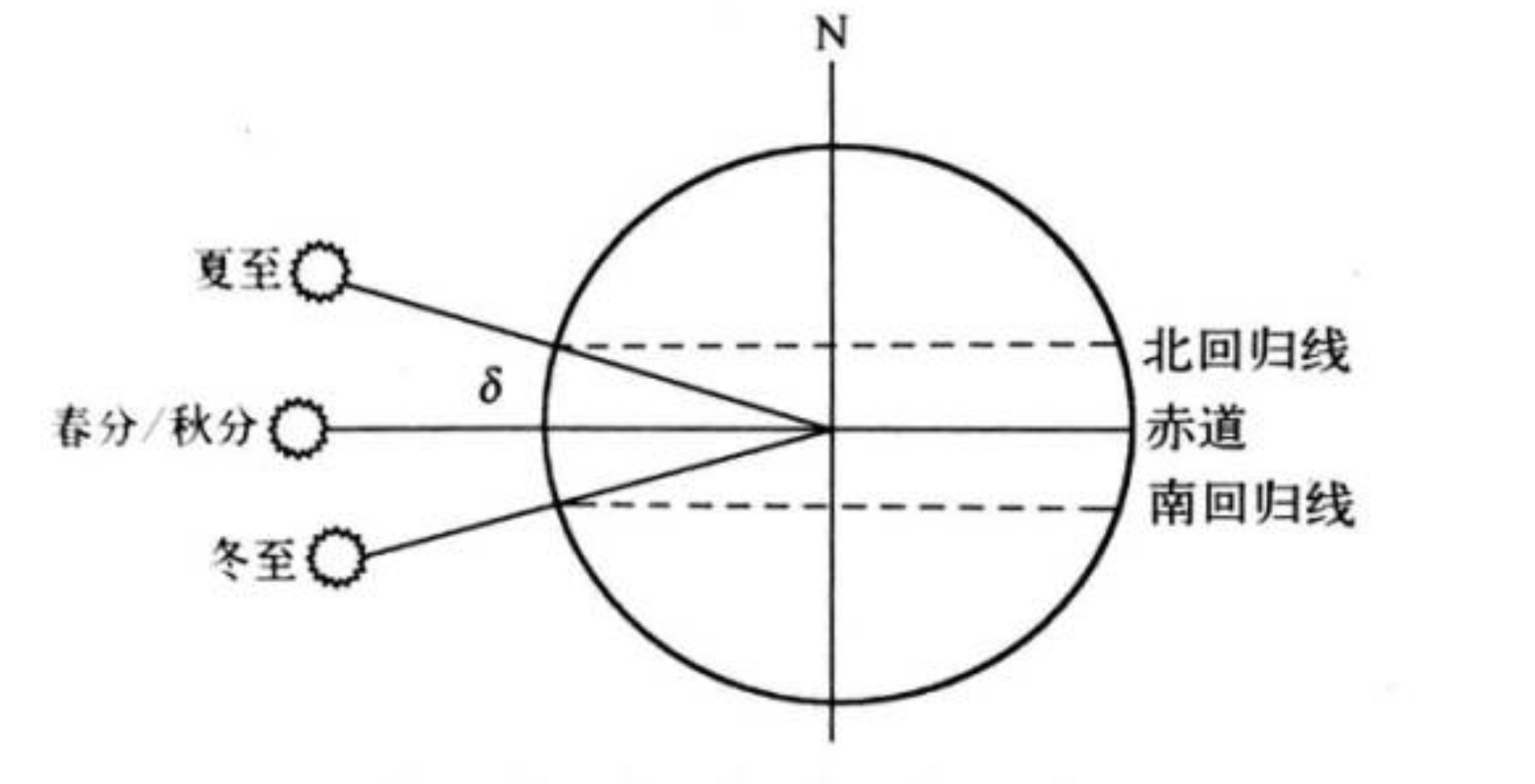
赤纬角 \(\delta\) 计算公式如下：

\[ \delta =23.45sin[360×(284+n)/365] \]

其中，n 是一年中的日期序号（1~365）。

地平坐标系

地平坐标系以观察者所处的地平面为基本平面。在地平坐标系中，我们用 高度角 和 方位角 定义某个时刻太阳在天空中的位。

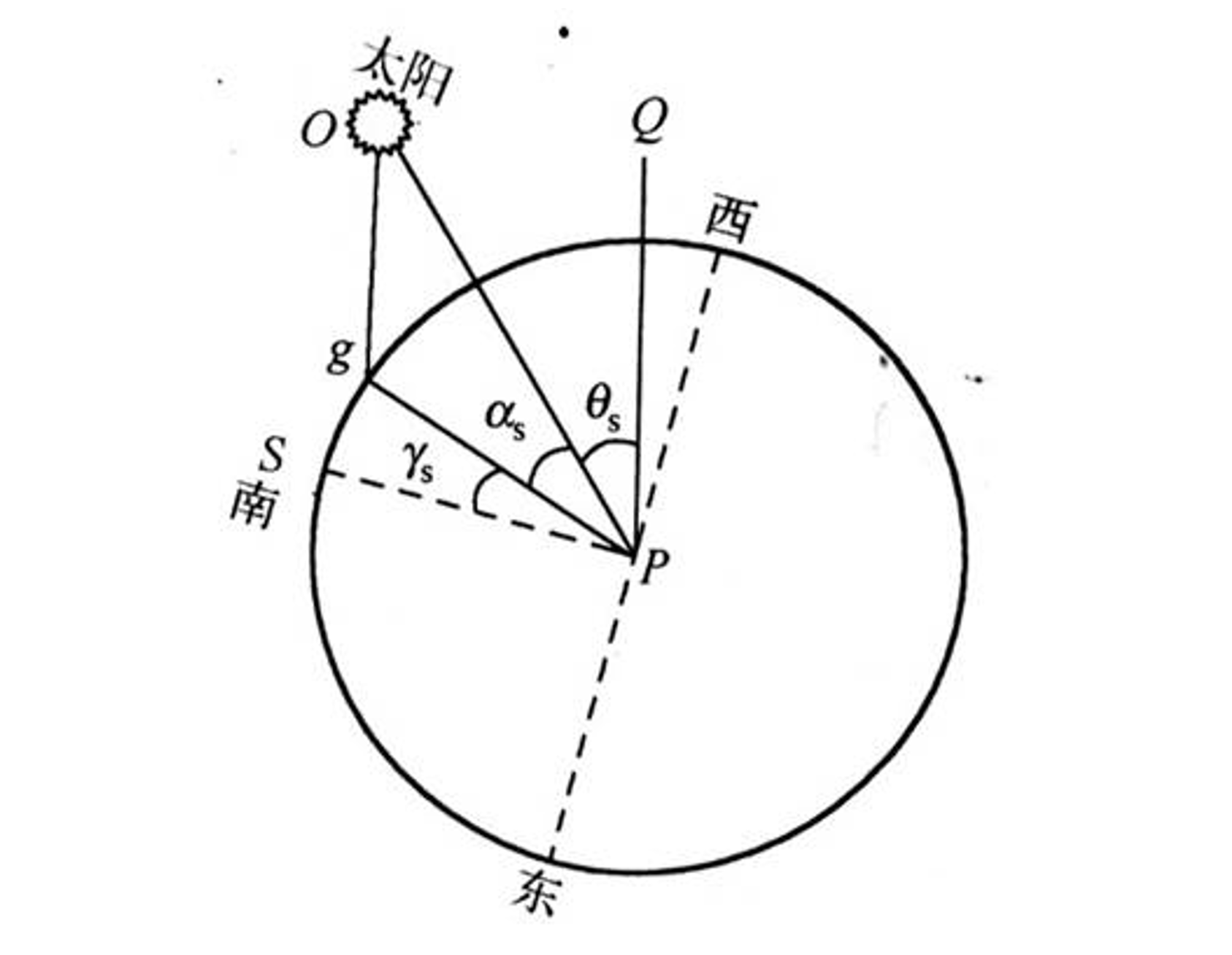
注：读此图需要有几何想象力，即圆是在纸面，太阳是在纸上方。

  • 高度角 \(\alpha_s\) ：太阳光线到观察者间的连线，与这条线在地面上的投影之间的夹角。
  • 方位角 \(\gamma_s\)：太阳光线到观察者间的连线在地面上的投影，与正南方向线之间的夹角。数值上正南方向为 0°，向西为正值，向东为负值。

高度角 \(\alpha_s\) 的计算公式：

\[ sin \alpha_s =sin \varphi sin \delta+cos \varphi cos\delta cos \omega \]

方位角 \(\gamma_s\) 的计算公式：

\[ sin \gamma_s=\frac{cos \delta sin \omega}{cos \alpha} \]
\[ cos \gamma_s=\frac{sin \alpha sin \varphi - sin \alpha}{cos \alpha cos \varphi} \]

法定时间与真太阳时

法定时间是指行政的时间（比如北京时间），而真太阳时是以正午 12 点的时间。

举个例子，北京和乌鲁木齐，太阳高度角最高时都是真太阳时 12 点；而在法定时间下，乌鲁木齐的太阳高度角最高（即正午）是 14 点左右。

参考与致谢

原文地址：https://wiki-power.com/
本篇文章受 CC BY-NC-SA 4.0 协议保护，转载请注明出处。