史密斯圆图与匹配电路基础
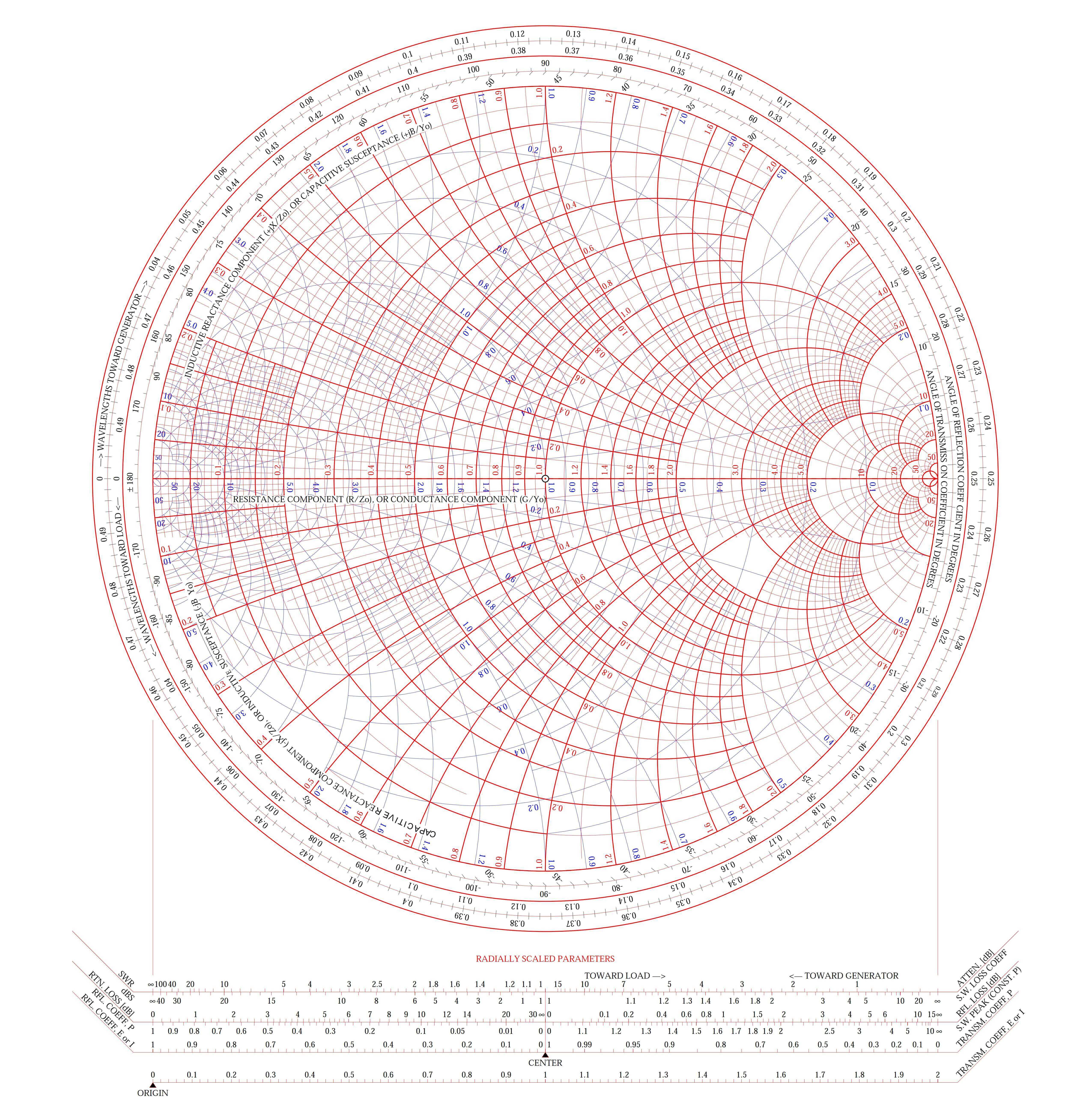
史密斯圆图是复数反射系数(伽玛 \(\Gamma\))的极坐标图。这种图以复数阻抗的实部和虚部同时绘制。其中,实部 R 的范围为 0 到无穷大(\(\infty\)),虚部 X 的范围为从负无穷大到正无穷大,都能绘制在一张图上。史密斯圆图能表现的参数与功能包括但不限于:
- 复阻抗
- 复反射系数
- 电压驻波比 VSWR
- 传输线效应
- 设计阻抗匹配网络
归一化阻抗
我们首先要把复阻抗转化为归一化阻抗,然后才能绘制在史密斯圆图上。归一化阻抗等于 实际阻抗 除以 系统阻抗:
在大多数情况下,系统阻抗为 50Ω,所以基本是实际阻抗除以 50Ω。举个例子,假如实际阻抗值是 (37+j55)Ω,则归一化阻抗的值算出来约为 (0.74+j1.10)Ω。
史密斯圆图详解
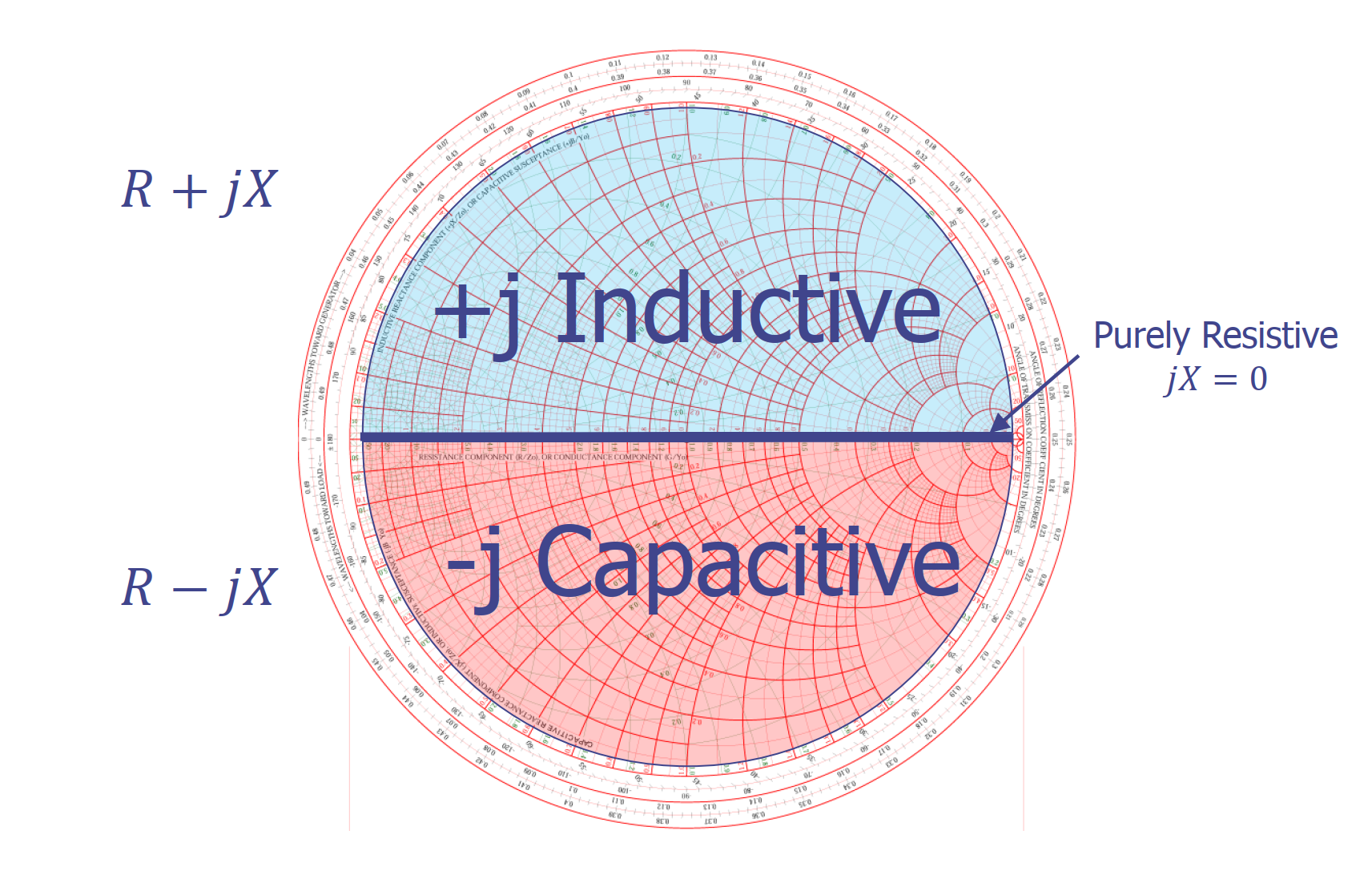
在史密斯圆图上,中间横向的主轴为纯电阻轴(R)。在此轴上,电抗恒为 0。在主轴上方的区域(R+jX),电抗呈现感性;而在下方的区域(R-jX),负电抗呈现容性。
关键点
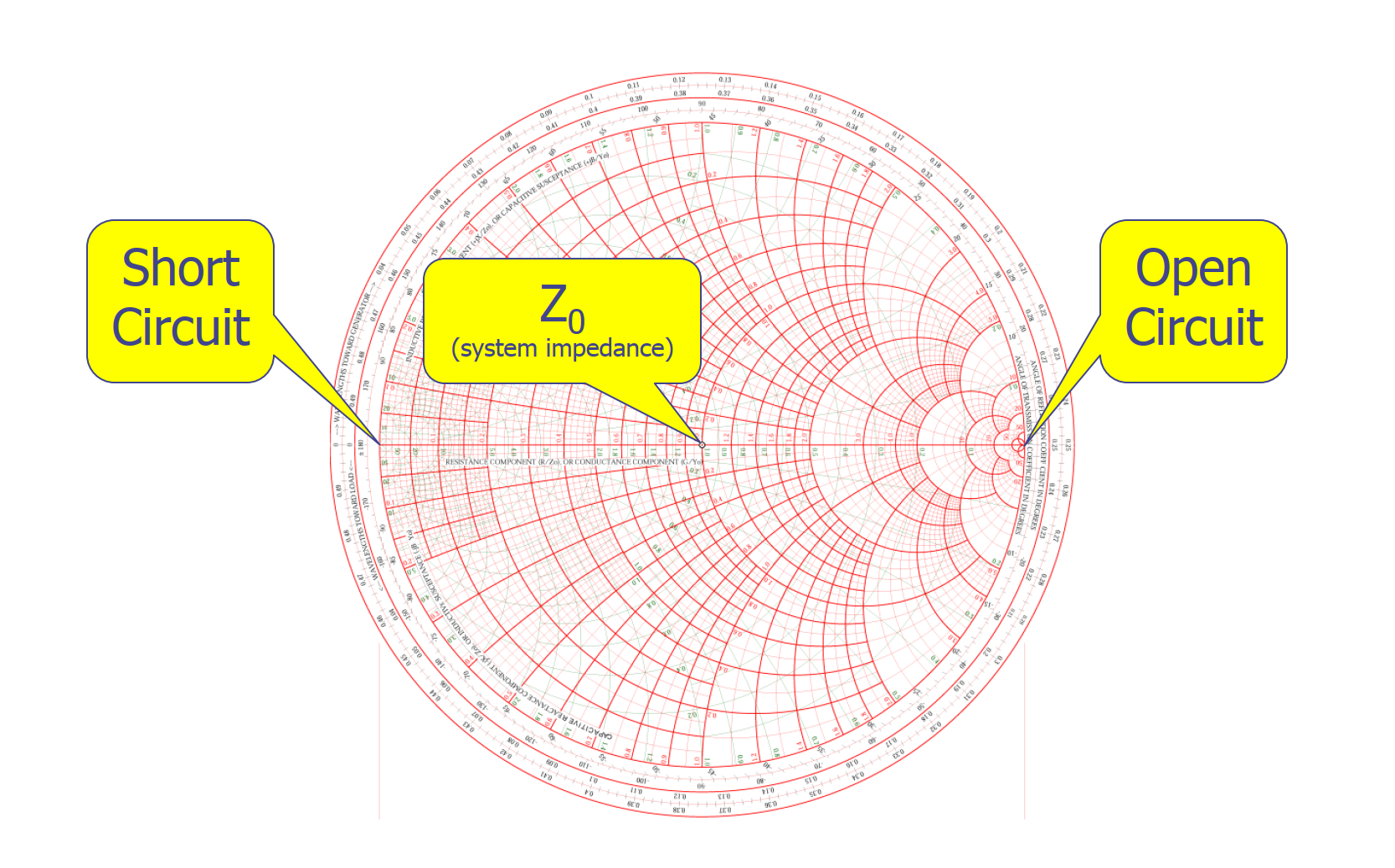
史密斯圆图上有一些关键点。最中间的点表示系统阻抗(在 50Ω 阻抗的系统中,中间这一点就代表 50Ω 阻抗值)。沿着主轴,最右边的点代表开路(阻抗无穷大);最左边的点代表短路(阻抗为 0)。
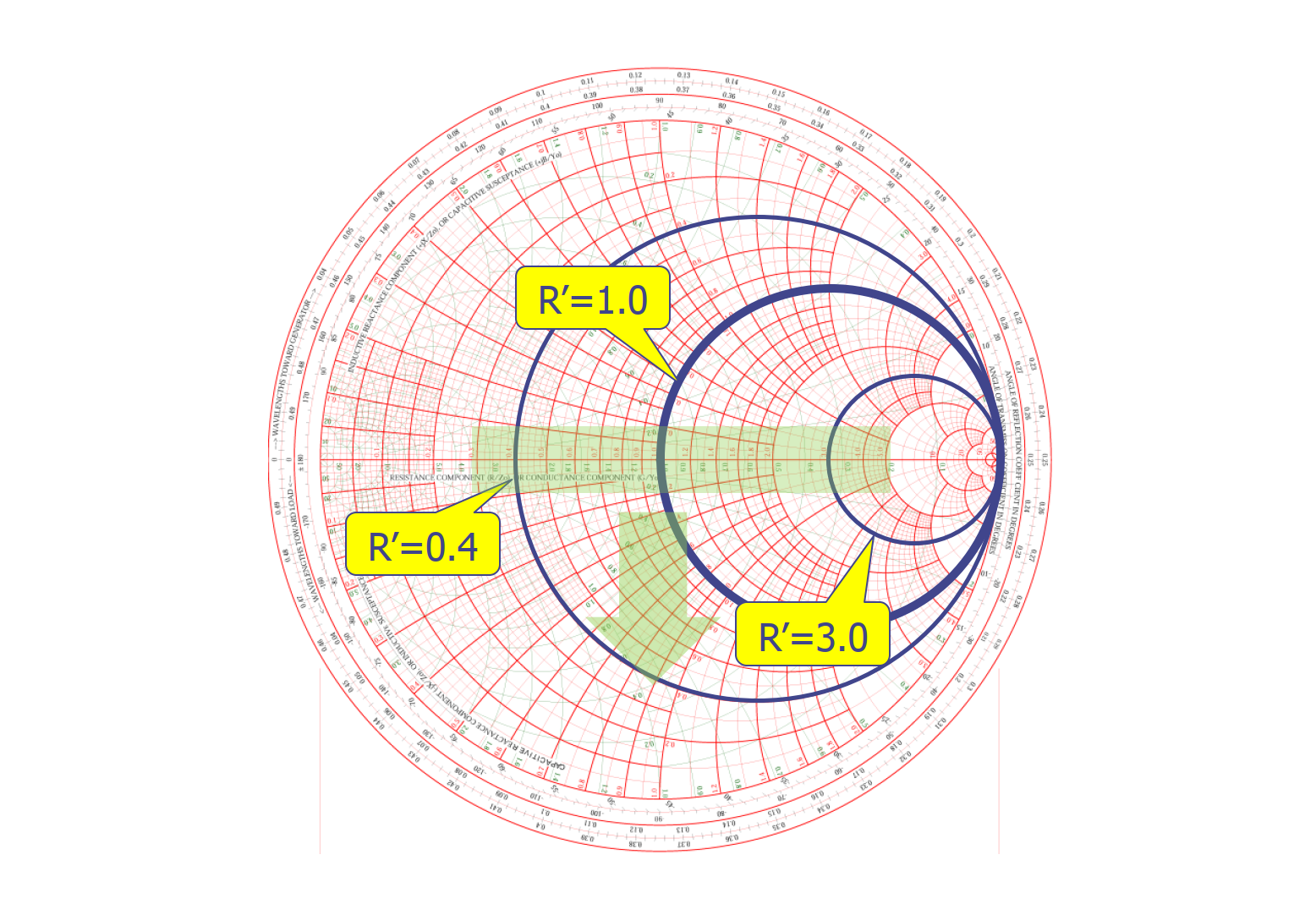
恒电阻圆
在恒电阻圆上的点,其归一化电阻(实部)为常数。比如其中通过中心点的圆,其电阻为 1(50Ω),即归一化阻抗的实部为 1。在图中呈现的,分别还有归一化阻抗的实部为 0.4 和 3.0 的恒电阻圆:
恒电抗弧
恒电抗弧从开路点延伸出来,落在弧上面的点,表示的是电抗的值,即复阻抗的虚部。弧度越大,电抗的绝对值越大,随着弧度变小,电抗的绝对值会越来越小,直到变为 0(落在纯电阻轴,不呈现感性或容性)。在图中呈现的,分别还有电抗值 ±0.5(虚部为 ±j0.5),±1.0(虚部为 ±j1.0)的恒电抗弧:
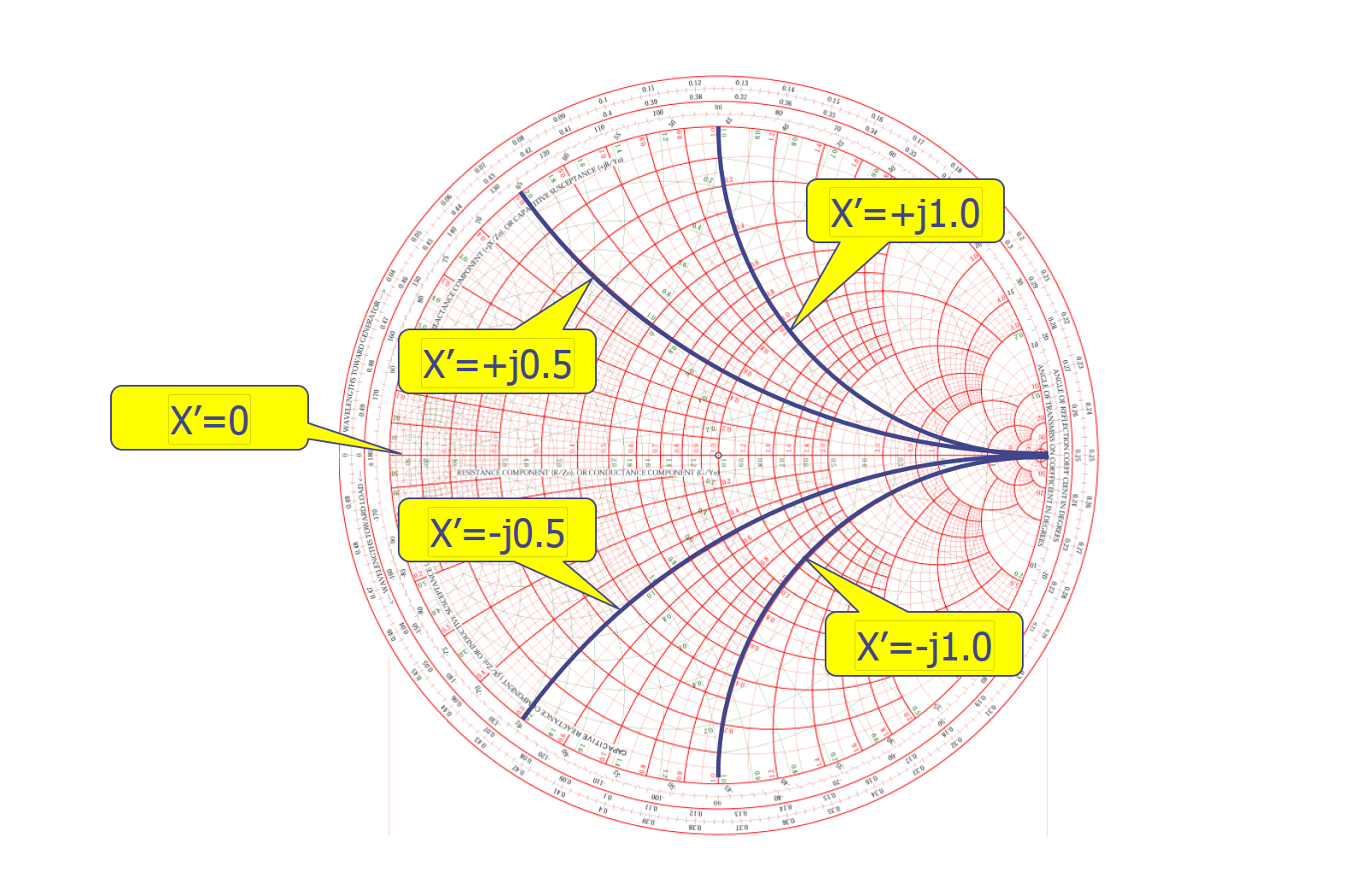
将复阻抗转换为复导纳
导纳(Admittance,Y)是阻抗的倒数,电导(Conductance,G)是电阻的倒数,电纳(Susceptance,B)是电抗的倒数。如果它们是复数,计算起来会非常复杂。但在史密斯圆图上,我们只需要以中心点为圆心,画一个经过复阻抗 Z' 点的圆,即可在它的另一侧找到对应的复导纳值 Y'。
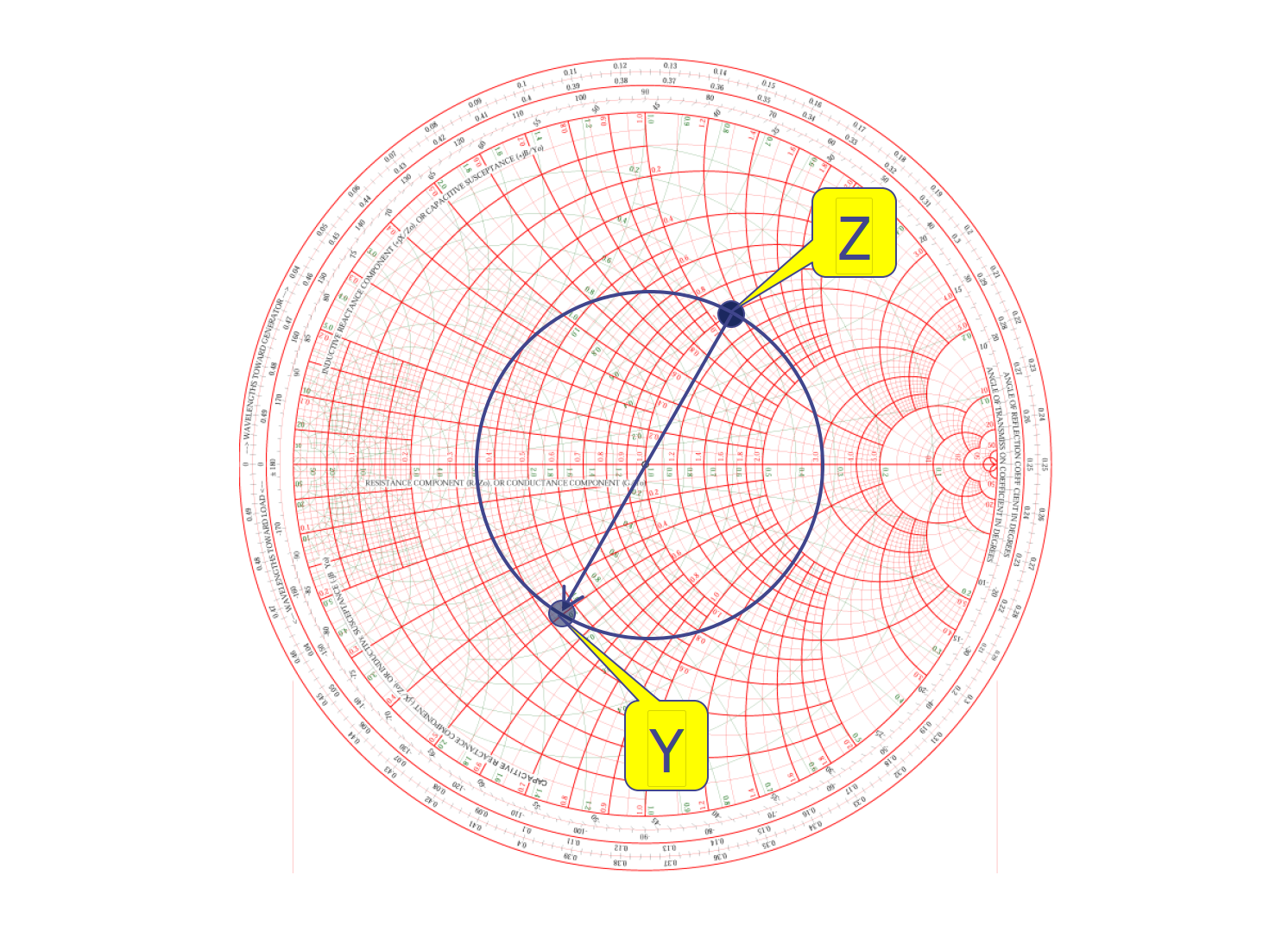
举个例子,假如 Z'=1+j1.1,则其对应的 Y'=0.45-j0.5。
如果是一条复阻抗曲线,那么可以把史密斯圆图旋转 180°,得到的曲线就是复导纳曲线了。
恒电导圆和恒电纳弧
完整的史密斯圆图上,还呈现了 恒电导圆 和 恒电纳弧,在下图以蓝线标记:
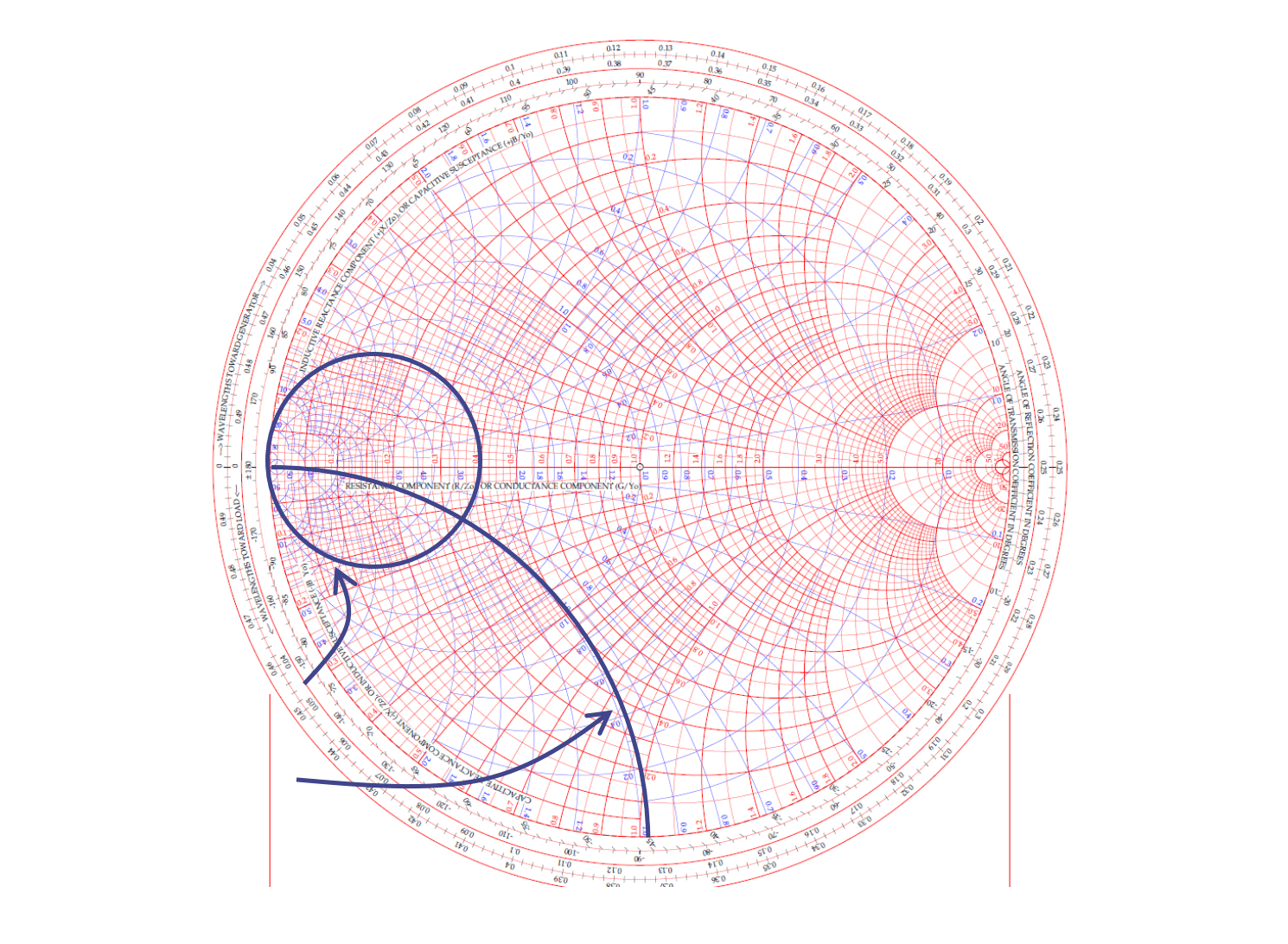
在史密斯圆图上标定一般值
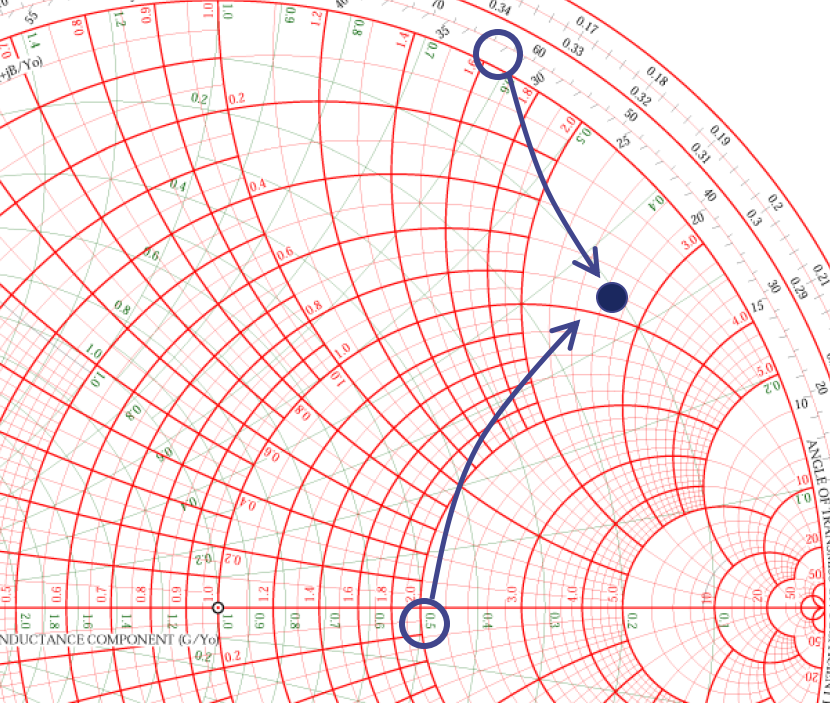
在史密斯圆图标定一般值,如 Z=25+j40。首先我们先按 50Ω 阻抗对其进行归一化处理,计算得 Z'=0.5+j0.8。由此,我们可以在图上寻找 R'=0.5 的圆与 X'=0.8 的弧,它们的交点就是所求的 Z':
史密斯圆图的径向缩放参数
一般来说,史密斯圆图底下还有径向缩放参数轴。假设图中有一复阻抗点,连接它与中心点,并沿着半径旋转到主轴上,投影到径向缩放参数轴上,如图:

在此轴上可读出一些参数:
- 电压驻波比(VSWR):2.3:1
- 回波损耗(Return Loss):8.10dB
- 反射系数(Reflection Coefficient)
- 电压:0.155
- 功率:0.39
不仅如此,我们也可以发现,出现在这个半径圆上的点,这些参数都是相同的。
驻波比与传输线的关系
在前文我们提到,在以系统阻抗(中心点)为圆心,到复阻抗点的距离为半径绘制的圆,圆上不同阻抗的点,其驻波比(SWR)都是相等的。在圆上转一圈的长度,相当于 1/2 波长值。所以,传输线长度每增加一半波长值时,复阻抗会沿着圆转多一圈。
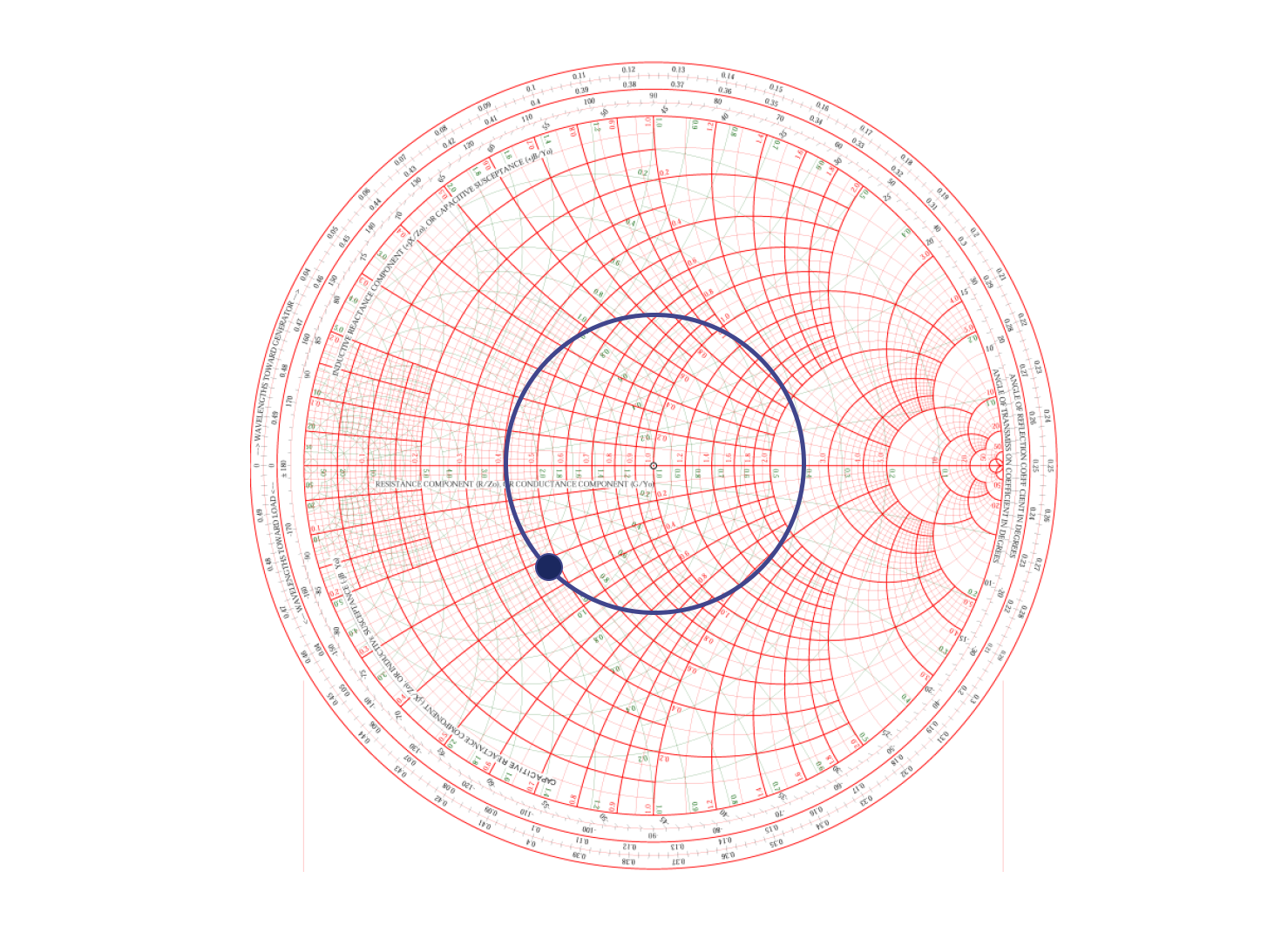
由此可得,从源端到天线的传输线的长度,应尽量控制在天线半波长的整数倍,才能使观测的阻抗与天线的实际阻抗不发生偏移。如果长度为一般值,则可在 SimNEC 仿真软件内使用传输线的模型进行补偿。
还有一个有趣的现象,如果末端为开路的传输线长度为 1/4 波长值(转半圈),那么它看起来就像是短路的;反之如果末端为短路的传输线,长度为 1/4 波长值,则观测出来的特征就像是开路的:
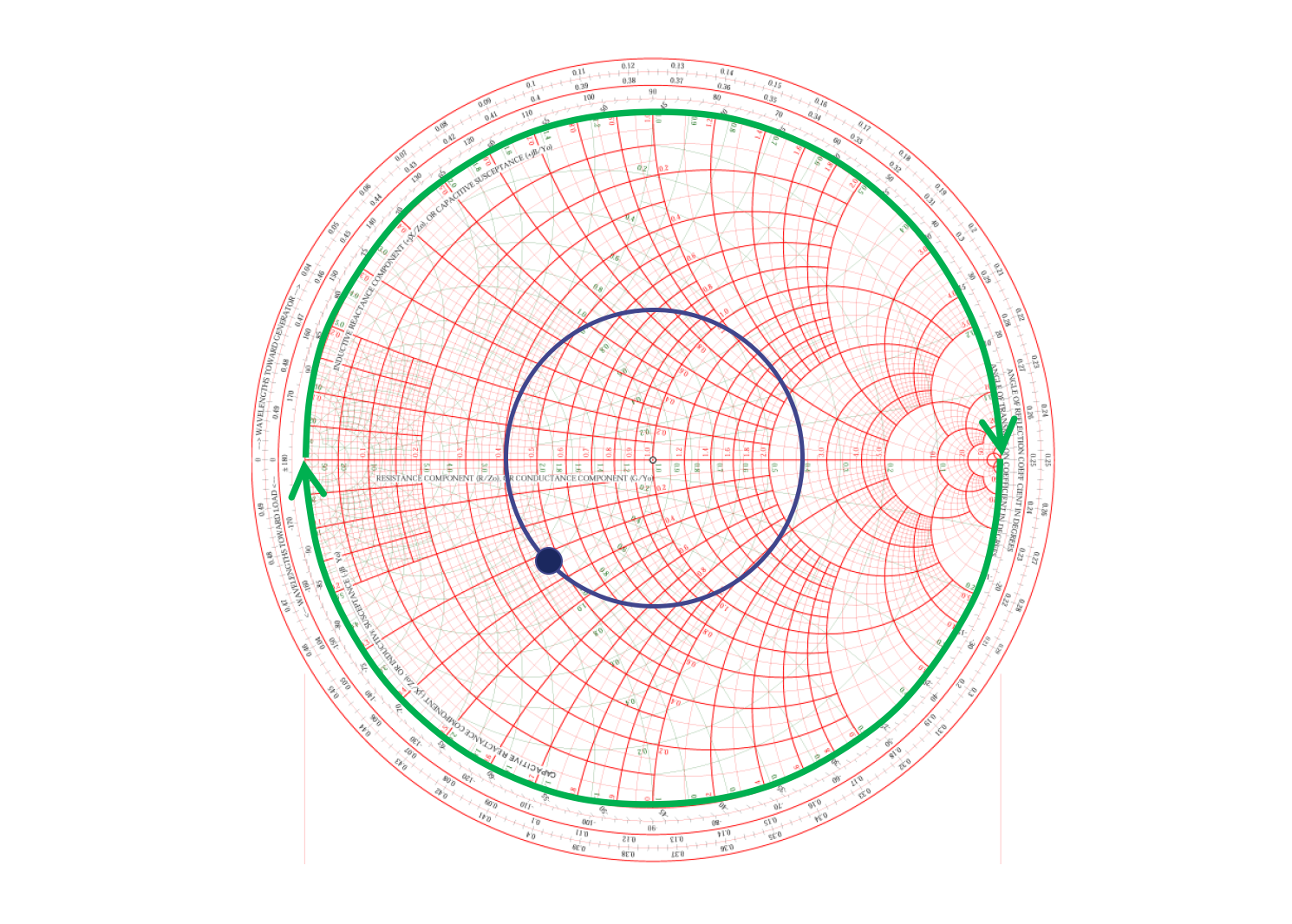
匹配电路的设计
通常我们会在电路中串联或并联电感和电容,移动复阻抗点,以匹配阻抗。
- 串联电感:沿恒电阻圆顺时针方向移动。
- 串联电容:沿恒电阻圆逆时针方向移动。
- 并联电感:沿恒电导圆逆时针方向移动。
- 并联电容:沿恒电导圆顺时针方向移动。
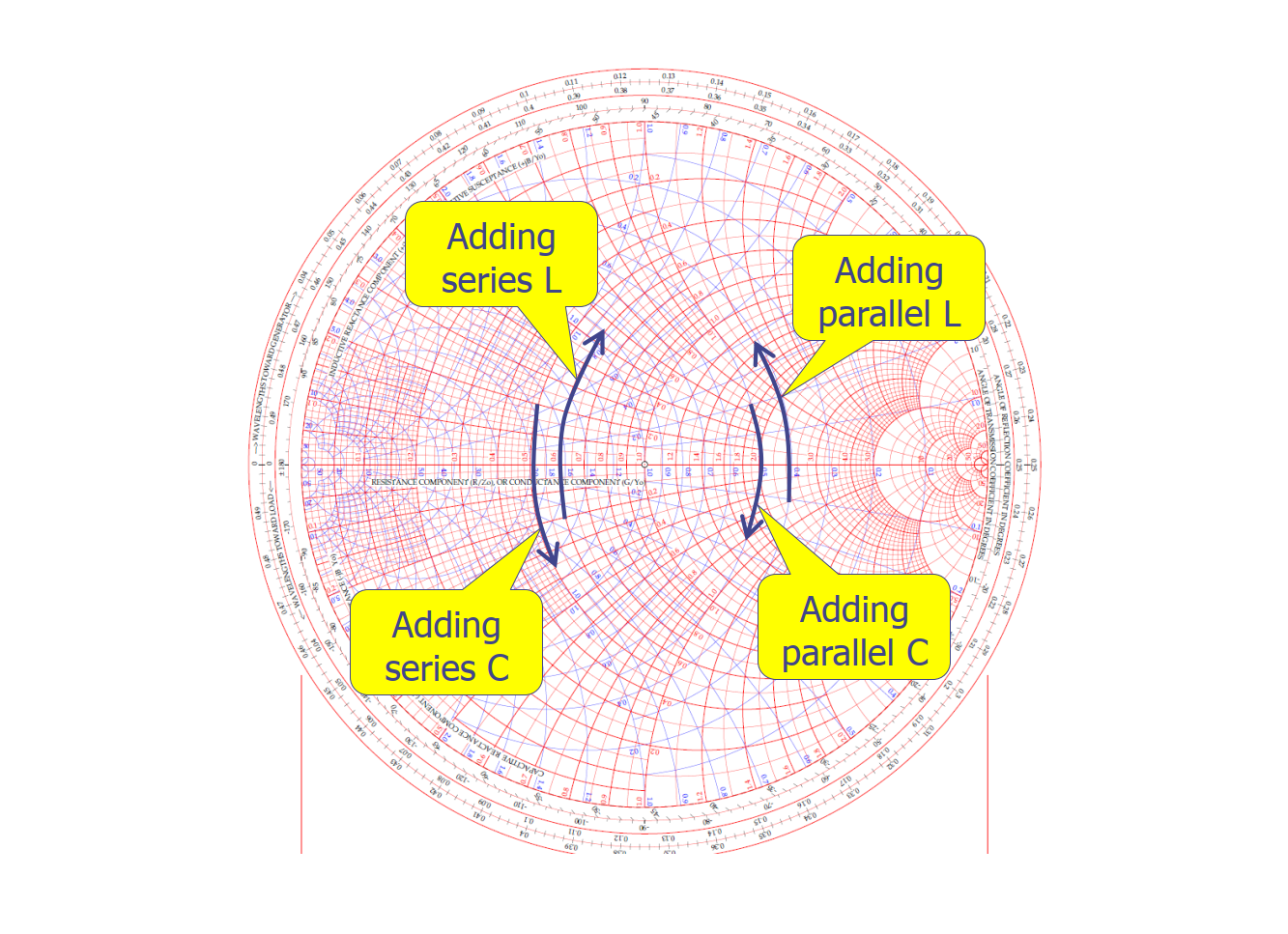
定性地看,不管是串联还是并联,加电感会使复阻抗点往上走,而加电容会往下走。
简单的 L 型匹配电路
假设当前电路实测复阻抗值为 \(Z_L\),我们需要把它调到理想的 \(Z_0\)(最好的是中心点,次之在 50Ω 的电阻圆上),则可以用电感或电容组成简单的 L 型状的匹配电路,使复阻抗点在史密斯圆图上移动。电感或电容的组合,取决于初始 \(Z_L\) 在史密斯圆图上的位置。可根据下图 \(Z_L\) 的分布,挑选合适的组合构建 L 型匹配电路:
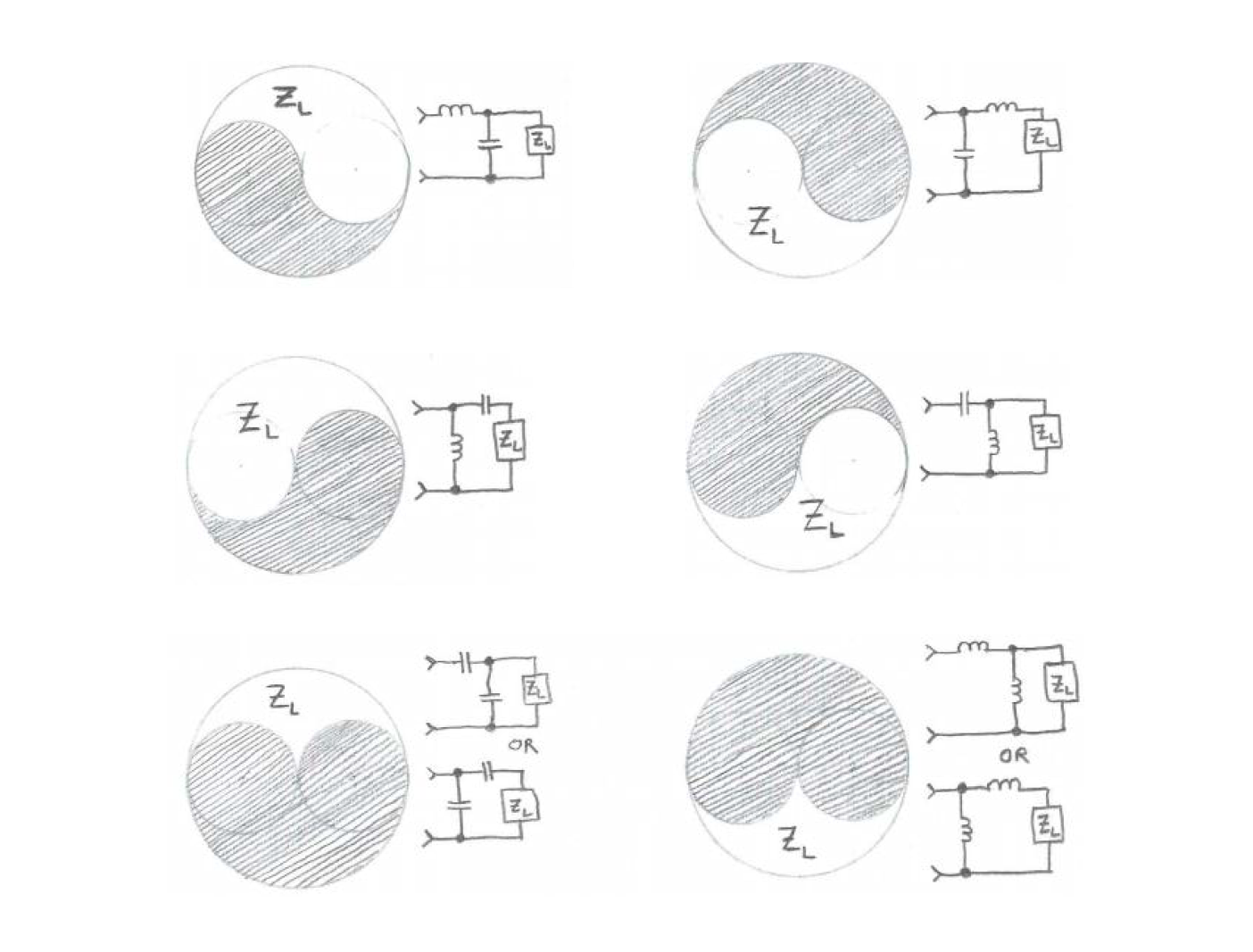
举个例子,初始复阻抗值 \(Z_L\) 如下图(黑点),我们可根据小图提供的 L 型匹配电路的构造,把它调到理想的 \(Z_0\) 上(红点):
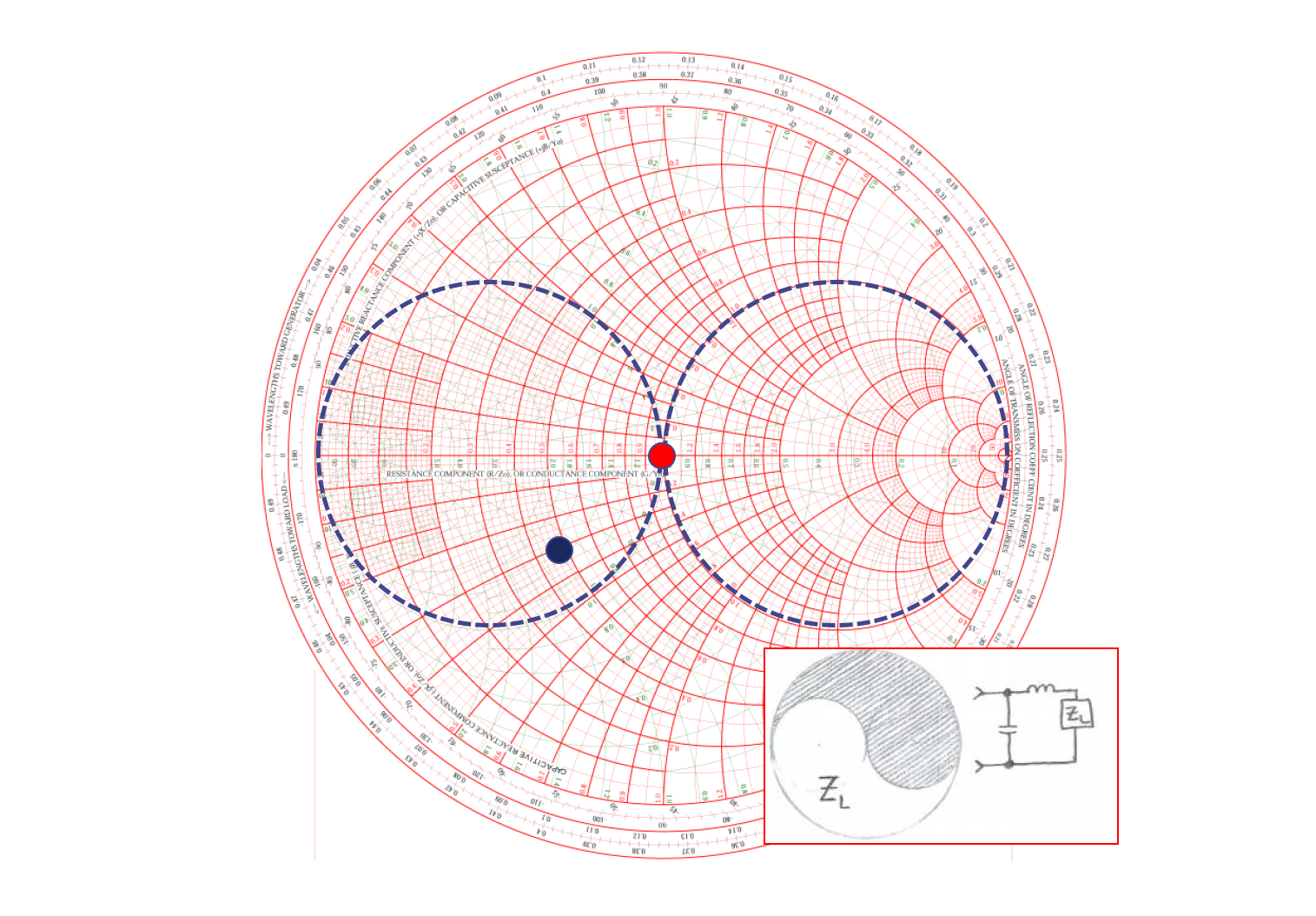
为了方便调试,我们在图上勾勒出标准恒导圆与恒阻圆。接下来的步骤可在 SimNEC 仿真软件内进行:
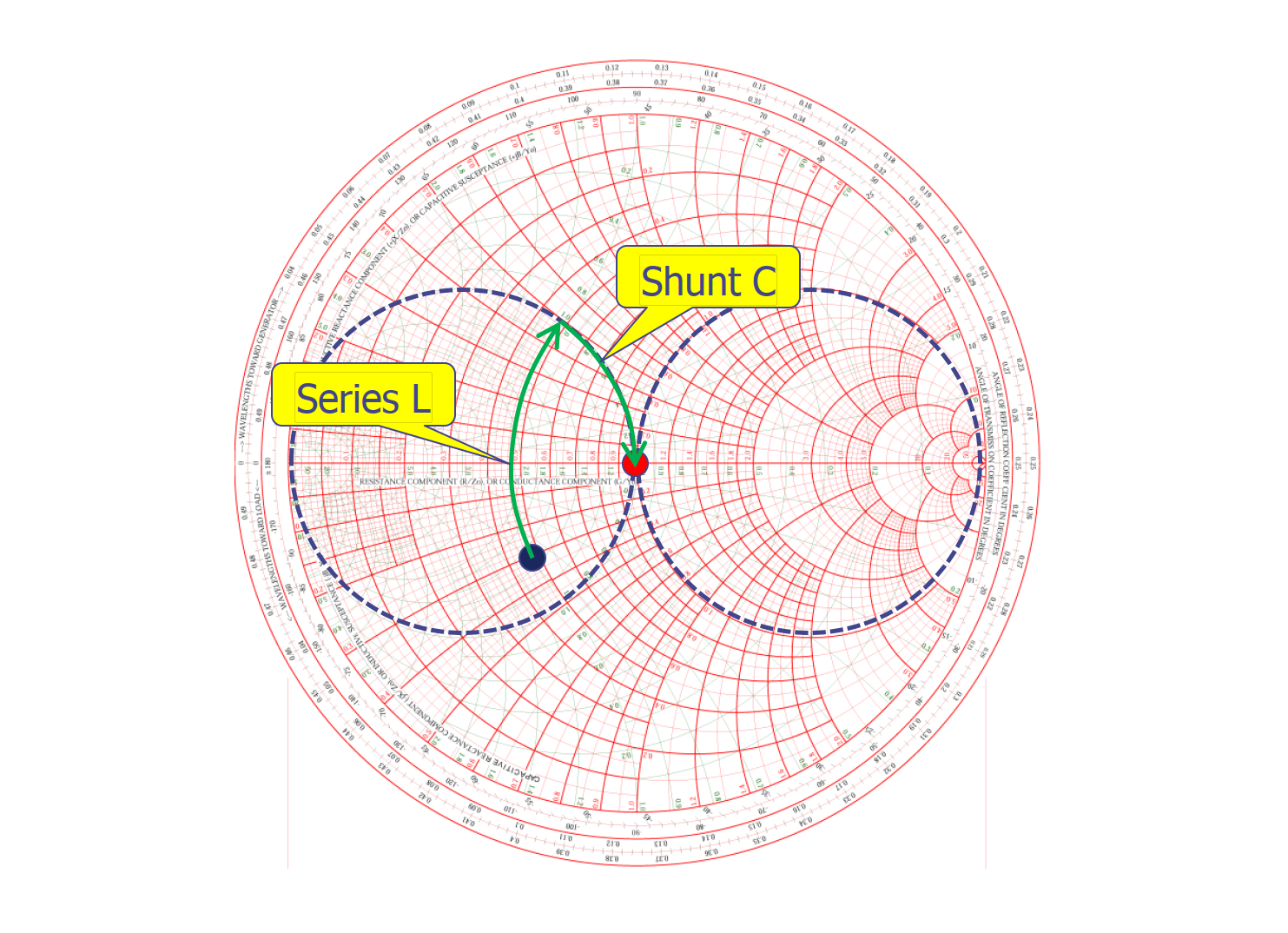
- 串电感,沿恒电阻圆顺时针方向移动,直到碰到恒导圆。
- 并电容,沿恒电导圆顺时针方向移动,直到中心点上。
方法大致可以归结为:从近负载端开始,添加第一个器件,使复阻抗点移动到标准恒导圆或恒阻圆上;添加第二个器件,使之沿着标准恒导圆或恒阻圆移动到中心点上。所选器件的值可在软件中读出。
对于实际匹配电路的调试,可跳转文章 一般天线匹配电路的设计。
参考与致谢
- 史密斯圆图:史密斯圆图的历史以及为什么对射频设计者如此重要
- Basics of the Smith Chart - Intro, impedance, VSWR, transmission lines, matching
- RF engineering basic concepts: the Smith chart
原文地址:https://wiki-power.com/
本篇文章受 CC BY-NC-SA 4.0 协议保护,转载请注明出处。