信号完整性 - 阻抗与电气模型

阻抗（Electrical Impedance, Z）是电路中电阻、电感、电容对交流电的阻碍作用的统称，定义为电压与电流之比（\(Z=V/I\)）。阻抗是一个复数，实部称为电阻，虚部称为电抗。其中电容在电路中对交流电所起的阻碍作用称为容抗，电感在电路中对交流电所起的阻碍作用称为感抗，容抗和感抗合称为电抗。

对于恒定的电压，阻抗越高，流经电流就越小，反之同理。极端情况下，开路的阻抗是无穷大的，短路的阻抗为零。在互连线中，阻抗是影响信号的关键因素。信号传播时，会不断根据瞬时阻抗做出相应的反应。

基本电气模型

在建立基本电气模型的过程中，我们会构想以下这几种理想的两端口元件：

理想电阻器
理想电容器
理想电感器
理想传输线

其中，理想阻容感的特性可以集中到一个点上，故称为 集总电路元件；而理想传输线的特性是沿着线分布的。目标是建立一个等效电路模型，使其阻抗尽可能贴近实际元件测得的阻抗。

时域中理想电阻器的阻抗

理想电阻器的阻抗是恒定的，数值大小与其电阻值相等，与电压、电流无关。

时域中理想电容器的阻抗

对理想电容器而言，两块极板之间储存的电荷与电压差有一定的关系，其容值的定义如下：

\[ C=\frac{Q}{V} \]

其中，C 表示电容值（单位 F），Q 表示极板间储存的电荷（C，库伦），V 表示两极板间电压（单位 V）。

电容的阻抗是通过其两端电压与流过的电流求得。实际上，电流并非真正流过电容，只是在电容两极板电压改变时，看似有电流在流动。

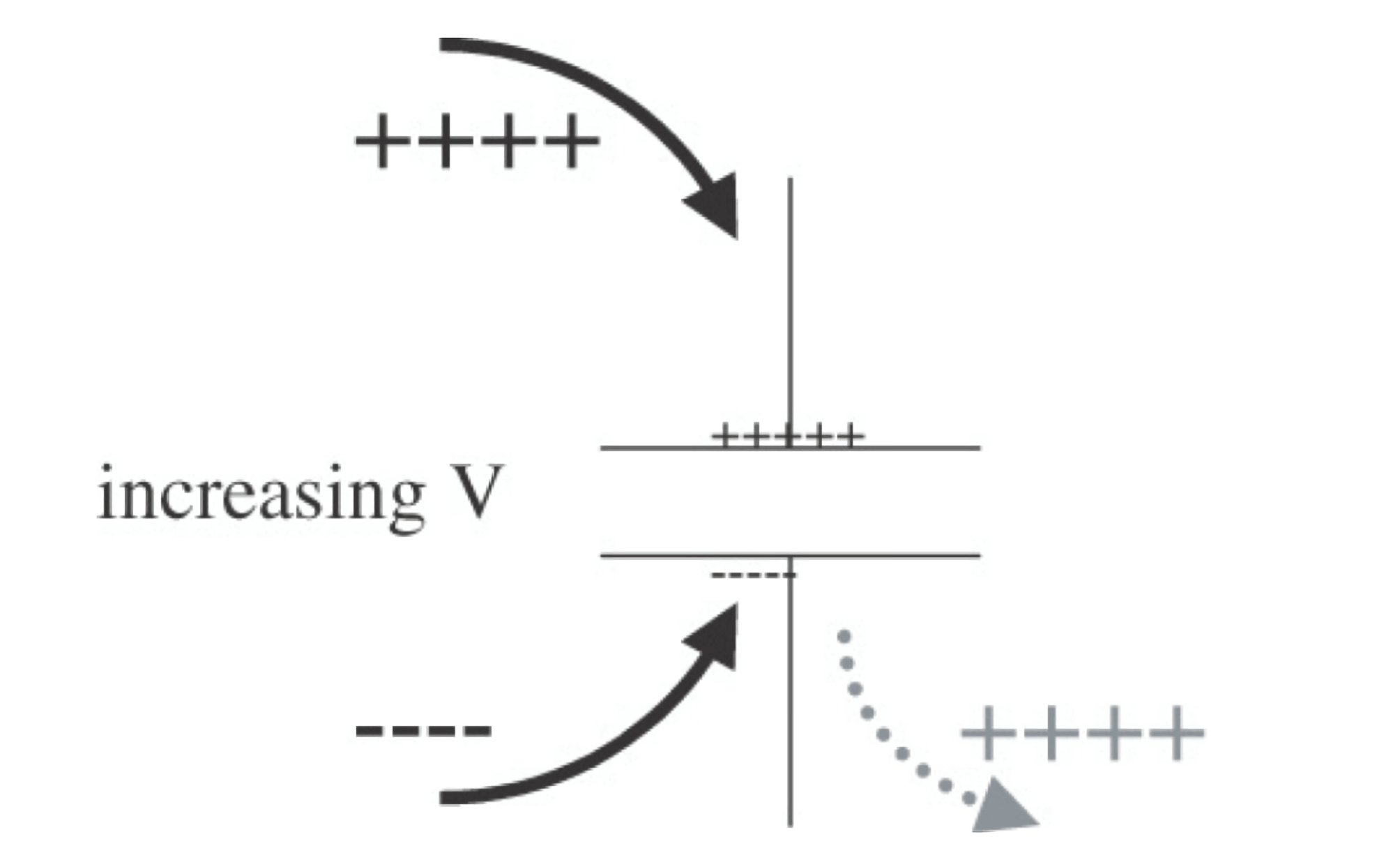
如上图所示，上极板增加了一些正电荷，下极板增加了一些负电荷的同时，把下极板原来存在的正电荷从推出去，这样看起来就像有电流穿过电容。这种在极化电介质中由束缚电荷位移形成的电流，称为 位移电流，它并不是真正的电流，而只是电荷的移动。其定义如下：

\[ I=\frac{dQ}{dt}=C\frac{dV}{dt} \]

从上式可看出，只有在电容两端电压发生变化时，才会有电流流过，如果电压固定不变，就不会有位移电流。

因此，理想电容的阻抗可以表示为：

\[ Z=\frac{V}{I}=\frac{V}{C\frac{dV}{dt}} \]

电容的阻抗与其两端电压波形有关。如果电压变化快（波形斜率大），则流过电流就大，阻抗也会越小；同理，当电压变化速率相同时，容值越大，阻抗就越小。

时域中理想电感器的阻抗

对理想电感器而言，其两端的电压定义如下：

\[ V=L\frac{dI}{dt} \]

其中，\(V\) 表示电感两端电压，\(L\) 表示电感值，\(I\) 表示流过电感的电流。可以看出，电感两端电压与流过电流变化的快慢有关，而电流快慢取决于两端电压差。两端电压差与电流变化速度谁是因谁是果，则取决于哪个是驱动源。电感的阻抗，可以表示为其两端电压与流经电流之比：

\[ Z=\frac{V}{I}=L\frac{\frac{dI}{dt}}{I} \]

如果流过电感的电流迅速增大，则阻抗就变得很大，反之同理；而如果电流为直流，则阻抗接近为 0。当然，电感的实际阻抗与电流的具体波形有着密切的关系。

频域中的阻抗

在上文可以看出，在时域中，电感器、电容器阻抗的计算公式都是相对复杂的函数，但是放在频域中分析，则会简单得多。

在频域中进行分析，正弦波是唯一存在的波形，所以只能通过研究它与理想元件的相互作用进行分析。正弦波的 3 个特征是：频率、幅度和相位。一般我们用弧度描述，角频率（\(rad/s\)）与频率（\(f\)）的关系为：

\[ \omega=2\pi f \]

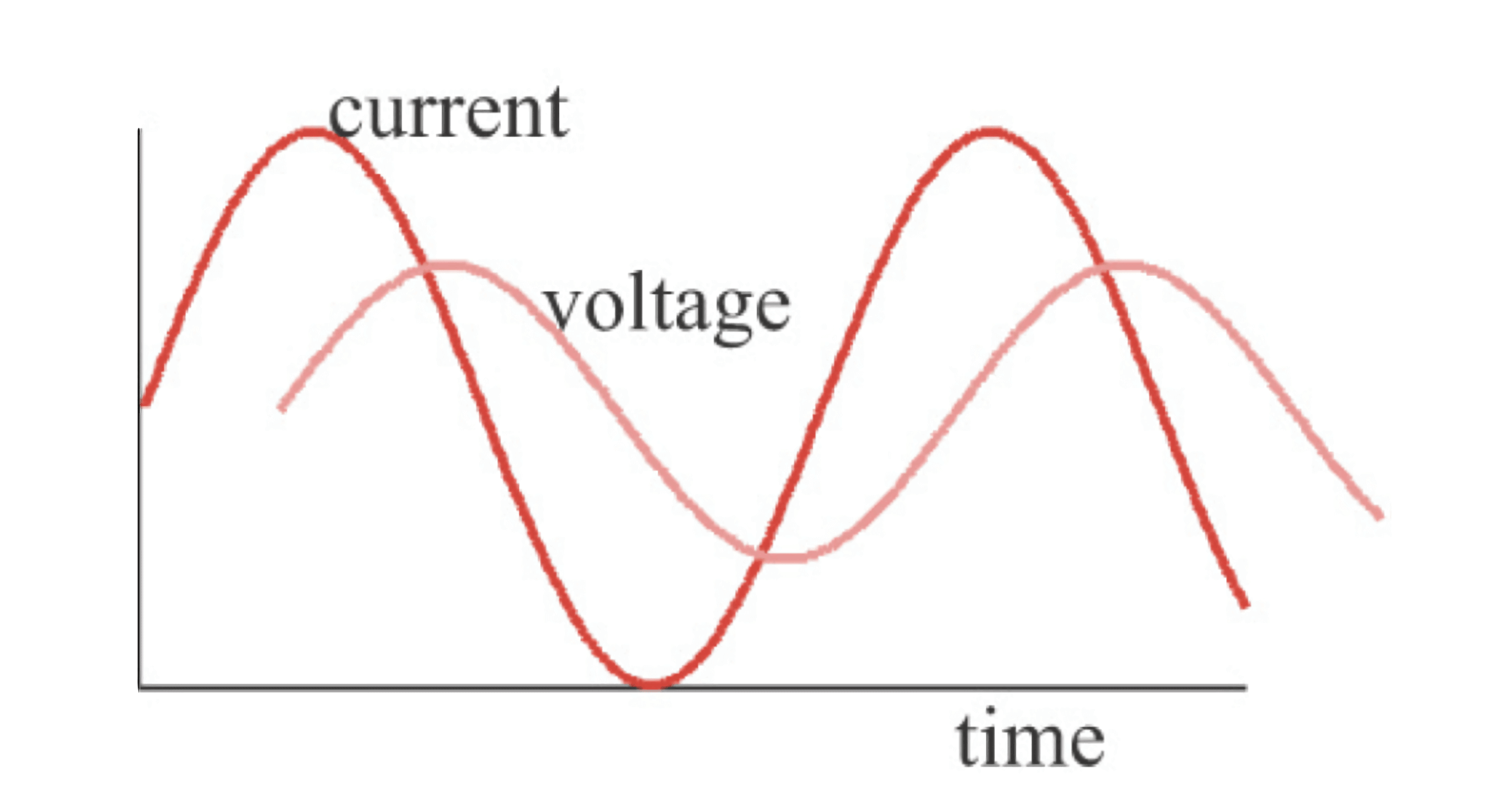
我们在理想元件两端加上正弦电压，观察流经电流情况。阻抗仍定义为电压与电流之比，只不过现在是电压正弦波和电流正弦波之比了。而因为理想元件和理想传输线都是线性元件，所以呈现的电流与输入电压的频率是一致的。

根据阻抗的定义，阻抗的幅值可以表示为：

\[ |Z|=\frac{|V|}{|I|} \]

同时，需要计算两个波形之间的相位差。在频域中，可以这样表示阻抗：在 10MHz 下，阻抗幅值为 20Ω，相位是 30°（电压比电流超前 30°）。这三个要素缺一不可，因为阻抗幅值和相位都与频率相关，会随着频率的变化而变。除此之外，也可用复数表示频域中的阻抗，把相位信息囊括进复数中，以此简化计算。

频域中理想电阻器的阻抗

我们接着分析在频域中理想元件的阻抗。因为频域中仅需处理正弦电压与电流，所以如果使用电流源，施加正弦电流流过电阻器，就会在其两端产生一个正弦电压，可以表示为：

\[ V=I_0 sin(\omega t) \cdot R \]

正弦电压为 R 与正弦电流的乘积。根据上面的公式，理想电阻器的阻抗可以表示为：

\[ Z=\frac{V}{I}=\frac{I_0 sin(\omega t) \cdot R}{I_0 sin(\omega t)}=R \]

其实理想电阻器的阻抗就是其电阻值，且与频率无关，相位差为零。此结果与在时域中的结论一致。

频域中理想电容器的阻抗

分析频域中理想电容器的阻抗，需要在其两端加一个正弦电压，所以流经的电流可以表示为：

\[ I=C\frac{d V_0sin(\omega t)}{dt}=C\omega V_0 cos(\omega t) \]

可以看出，即使电压不变，电流也会随频率而变，频率越高，流经电流幅度越大。也就是说，电容器的阻抗会随频率升高而减小，可以表示为：

\[ Z=\frac{V}{I}=\frac{V_0 sin(\omega t)}{C\omega V_0 cos(\omega t)}=\frac{1}{\omega C}\cdot \frac{sin(\omega t)}{cos(\omega t)} \]

可见，阻抗幅值为 \(\frac{1}{\omega C}\)，角频率增加时，阻抗会减小。

因为阻抗的相位是电压正弦波与电流正弦波的相位差，在电容器中就是正弦与余弦之间的相位差 \(-90°\)，在复数中就是 \(-i\)，所以用复数形式表示电容器阻抗就是 \(\frac{-i}{\omega C}\)。

举个实际的例子，如果有一个理想的 10nF 去耦电容器，则在 \(1kHz\) 下其阻抗就是 \(\frac{1}{2\pi \cdot 1kHz \cdot 10nF}\approx 16kΩ\)。如果频率降为 \(1Hz\)，则阻抗约为 \(16MΩ\)。

频域中理想电感器的阻抗

对频域中理想电感器，我们施加正弦电流，则产生电压为：

\[ I=L\frac{d I_0sin(\omega t)}{dt}=L\omega I_0 cos(\omega t) \]

当电流幅度固定不变时，频率越高，两端电压就越大。也就是说，随着频率升高，需要更高的电压，才能维持电流幅度不变。电感器的阻抗随频率升高而增大，根据阻抗的定义可表示为：

\[ Z=\frac{V}{I}=\frac{L\omega I_0 cos(\omega t)}{\omega I_0 sin(\omega t)}=\omega L \cdot \frac{cos(\omega t)}{sin(\omega t)} \]

可见，由于电感器的特性，频率越高，交流电流流经电感器就变得越困难。

与电容器同理，对于电感器的阻抗，其相位是 \(+90°\)，用复数 \(i\) 表示。电感器阻抗复数表现形式为 \(Z=i\omega L\)。

在实际去耦电容器中，其自身形状和封装会带来寄生电感，大约为 \(2nH\)。如果视其为理想电感器，那么在 \(1GHz\) 下，会带来 \(Z=2\pi \cdot 1GHz \cdot 2nH=12Ω\) 的阻抗。因为在相同频率下，理想电容器的阻抗仅为 \(0.01Ω\)，故可解释为在高频下，实际电容器表现为感性。

参考与致谢

《信号完整性与电源完整性分析》

原文地址：https://wiki-power.com/
本篇文章受 CC BY-NC-SA 4.0 协议保护，转载请注明出处。