跳转至

信号完整性 - 时域与频域

一般来说，我们会从时域和频域两个角度，分别对信号进行分析。

时域

时域是真实世界存在的域，按时间顺序呈现。例如，在某个时钟信号的时域图中，可以观察到两个重要的参数，波形的周期和上升沿：

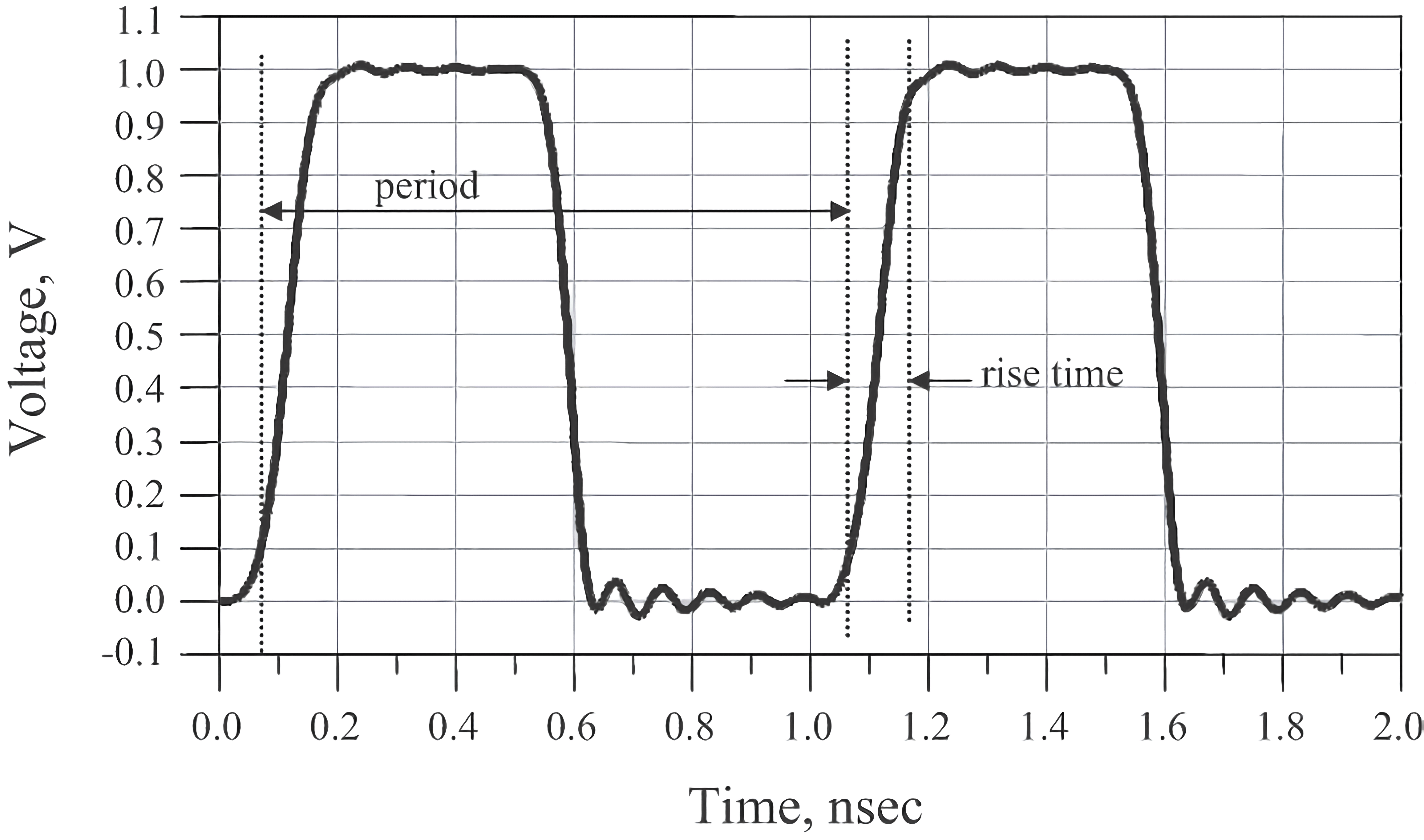
时钟周期即信号循环重复一次所花的时间，通常它的单位是纳秒级，时钟频率就是 1s 内循环的次数，即周期的倒数。例如，周期为 1ns 的时钟信号，频率就是 1/10ns=0.1GHz。

上升沿，通常定义为信号以最高点为标准的 20% 跳变到 80% 所花的时间（有时也会定义为 10% 到 90%）。下降沿通常比上升沿要短，这是因为典型 CMOS 结构中，N-MOS 比 P-MOS 导通速度要快，所以下降沿通常比上升沿短，也更容易产生信号完整性问题。

频域

频域是一个存在于数学定义中的域。通常在频域中使用正弦波，因为时域中的任何波形，都能用正弦波合成出来。

频域可以用更简洁的语言描述相同的信息。如下图可见，左边是时域中对正弦波的描述，正弦波可以用频率、幅度、相位这 3 个参数完全表示出来；而右边是频域中的描述，频率和幅度可以仅用一个点表示出来（在大多数场合会忽略相位的使用）：

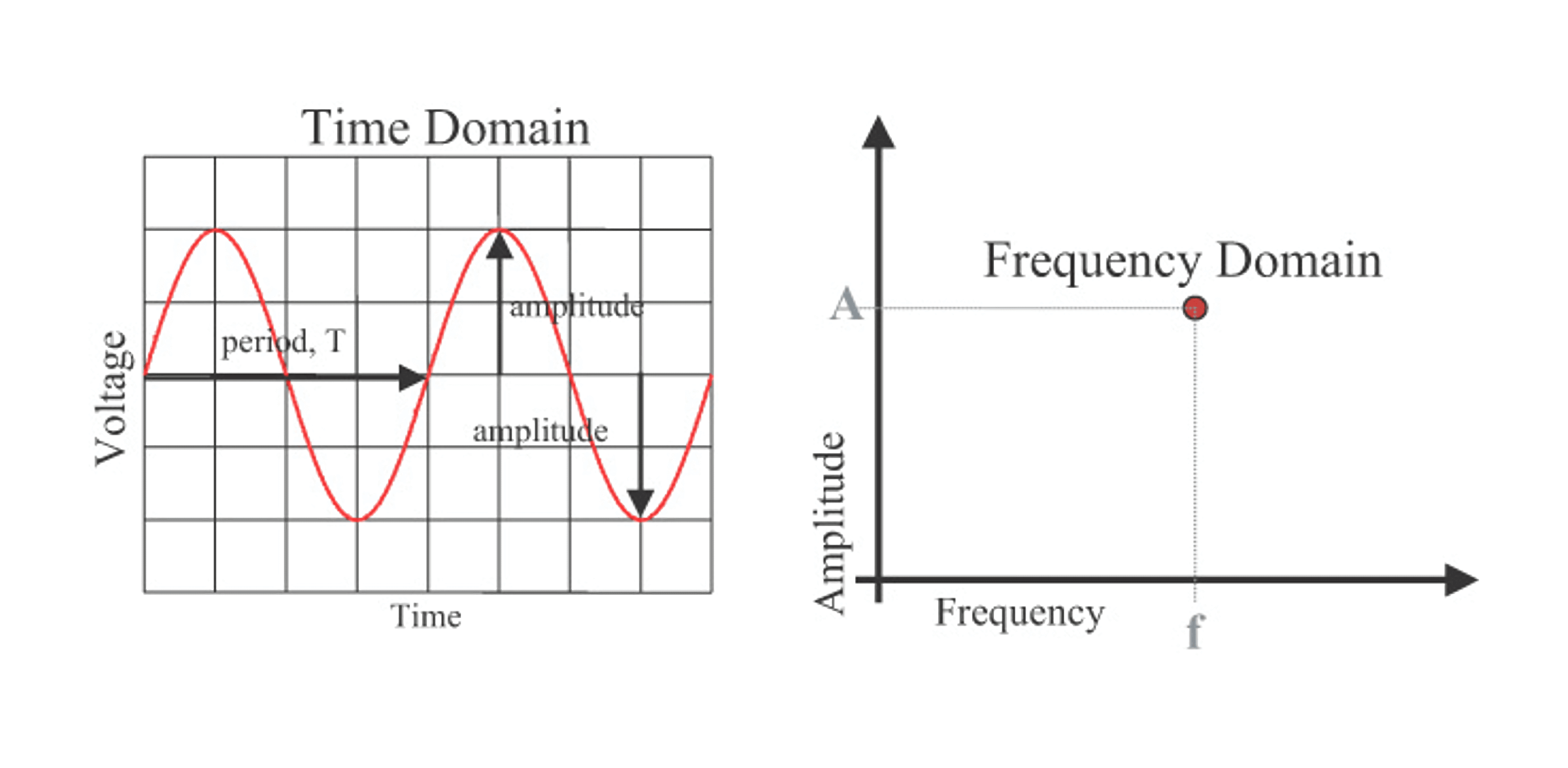
这样，在频域中表示一个正弦波就只需要一个点。如果有若干个频率点，那么这个集合就称为频谱。

将一般互连的电气问题放在频域中，并使用正弦波描述，会变得更容易理解并解决。

时域到频域的变换

从时域到频域，转换方法就是傅里叶变换。傅变有三种类型：傅里叶积分（FI）、离散傅里叶变换（DFT）、快速傅里叶变换（FFT）。

傅里叶积分用于将时域内的理想数学表达式变换为频域表示，是将时域时间轴从负无穷到正无穷积分，得出从零到正无穷上连续的频域函数。

但实际上时域的波形是由一系列离散点组合而成的。这时候使用离散傅里叶变换，可以把波形转换到频域中（前提是时域为周期性的）。不比傅里叶积分，傅里叶变换只需要通过求和就可以实现转换。

快速傅里叶变换使用了快速矩阵代数学的方法，只应用于时域中数据点个数是 2 的整数次幂的情况（如 256、512、1024 点）。根据计算点个数的数量，计算速度可以比普通离散傅里叶变换快很多。

需要注意的是，快速傅里叶变换要求信号是周期重复的，所以需要对原始信号进行相干采样，或在采样后加窗处理。

频域到时域的逆变换

频域包含波形中所有正弦波的频率和幅度，如果要获取它的时域波形，那么只需要将每个频率分量逆变换乘它的时域正弦波，再叠加起来即可，这个过程称为傅里叶逆变换。

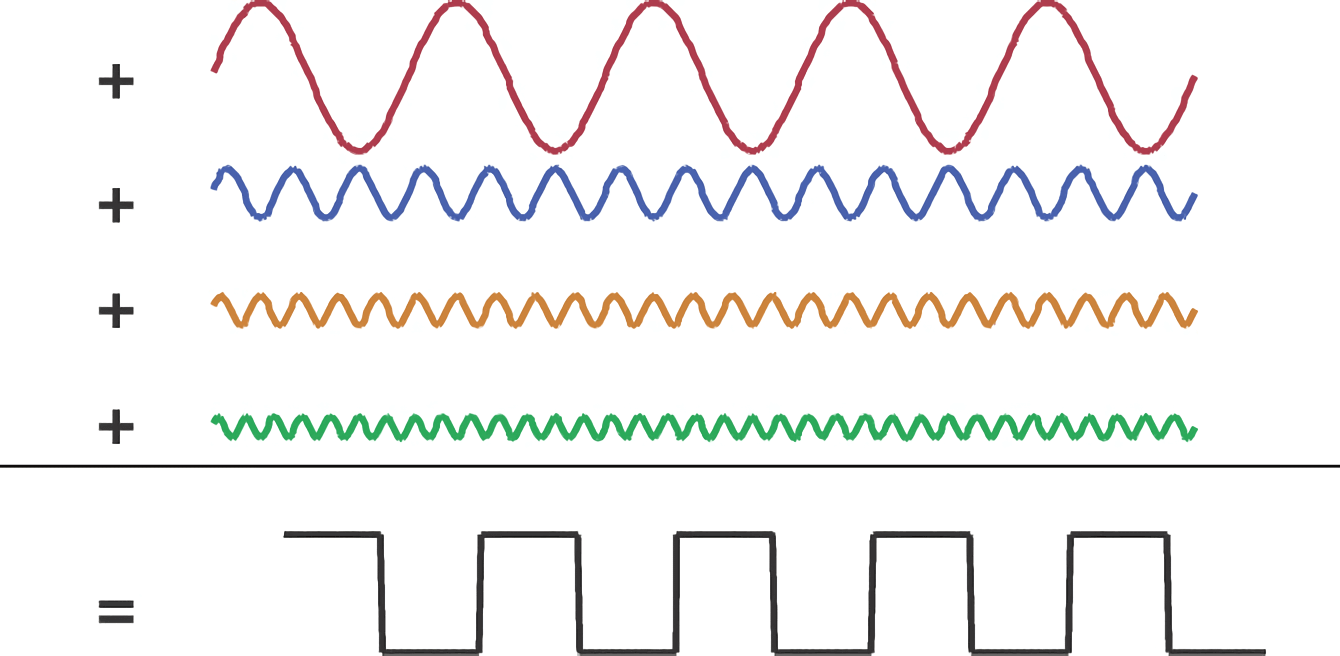
方波就是正弦波的多次谐波分量叠加，叠加次数越多，上升沿越陡，越接近于理想方波：

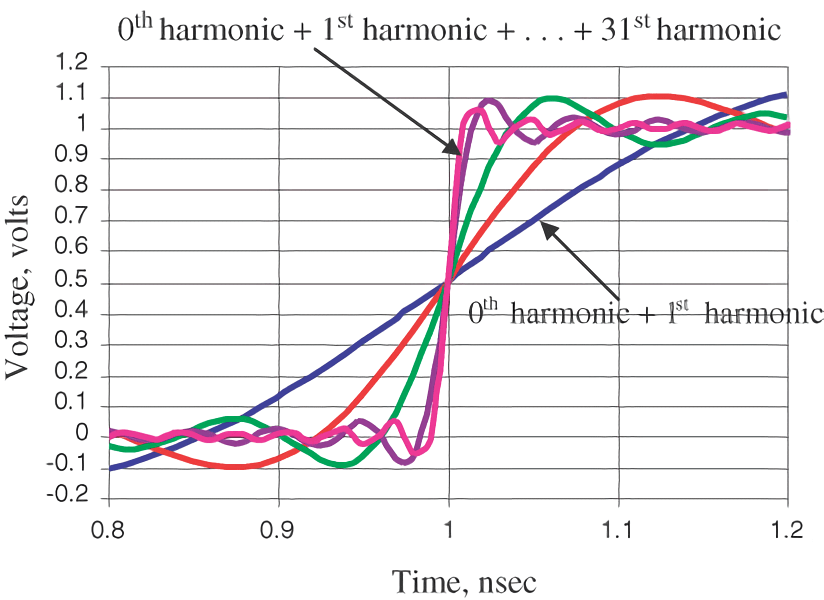
带宽与上升沿

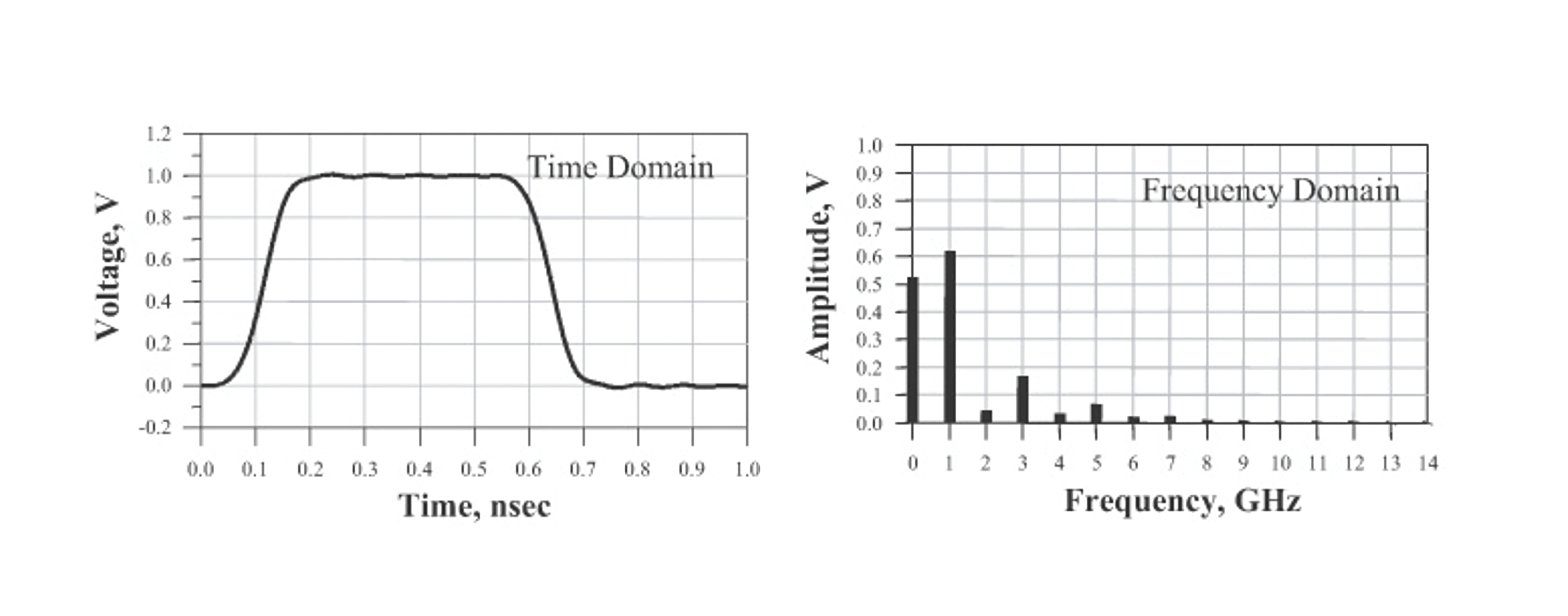
带宽表示频谱中最高 有效 正弦波频率分量值（因为在数字信号中，最低频永远是直流），表示信号频谱中的频率范围。带宽的选择对时域波形的最短上升沿有直接的影响。以理想方波为例，带宽越大，上升沿就会越短，波形就越接近理想方波。

注意，「有效」表示信号谐波幅度高于相同基频理想方波中对应谐波幅度的 70%。

例如，如果只用第 0、1、3 次谐波合成时域波形，那么波形的带宽为第 3 次谐波的值即 3GHz。

根据实验得出的经验法则，带宽与上升沿的关系为 \(BW=\frac{0.35}{RT}\)，其中 BW 为带宽（GHz）,RT 为 10%-90% 上升沿（ns）。举个例子，如果信号的上升沿为 0.1ns，那么信号的带宽就是 0.35GHz，反之也成立。（注意单位对应，GHz 对应 ns，MHz 对应 us）

参考与致谢

原文地址：https://wiki-power.com/
本篇文章受 CC BY-NC-SA 4.0 协议保护，转载请注明出处。