信号完整性 - 传输线 🚧
传输线是一种理想元件,由任意两条一定长度的导线组成,分别称为 信号路径 和 返回路径(参考路径)。传输线有两个重要的特征:特性阻抗 与 时延。
信号的传输方式
观察信号的传输,需要同时看信号路径与返回路径。如何确定信号路径和返回路径呢?如果两根线是一模一样的(例如双绞线),则没有严格的区分;如果是微带线,一般会指定平面为返回路径。需要注意的是,在信号完整性的范畴中,我们会用「返回路径」这个概念代替「接地」,因为需要分析的情况远比单纯「接地」复杂得多。
信号进入传输线后,将在其中以介质中的光速传输。我们可将信号表示为信号路径和返回路径上,相邻两点间的电压差:
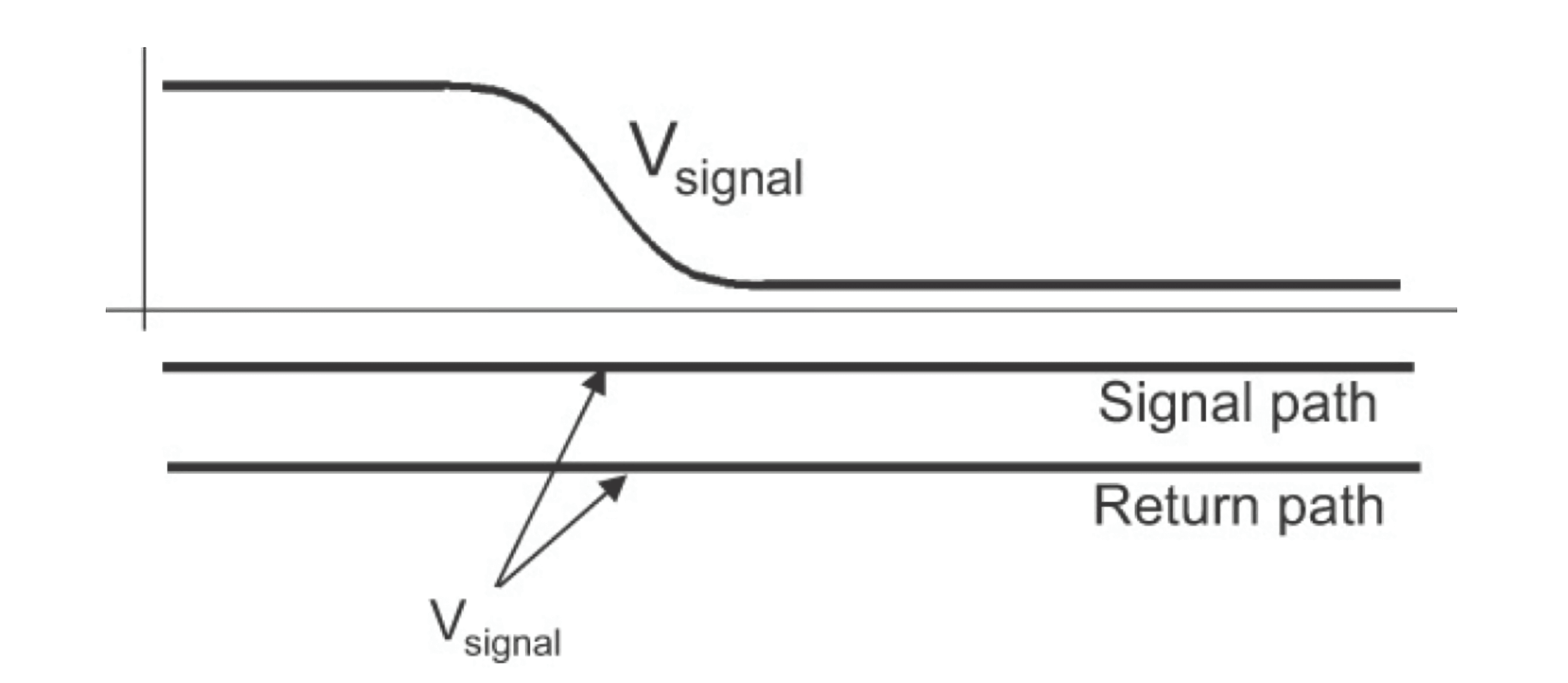
如果假设一对足够长且末端开路的传输线,分别在源端和末端都串接电流表,检测信号电流。在实际实验中可以观察到,当信号刚开始进入信号路径时,在返回路径上就已经开始检测到电流了。所以,电流的回路并非从从头到尾从源端到末端、再从返回路径流回来,而是通过信号和返回路径产生的电位差而产生电流(类似电容的充电)。随着信号的传播,产生电流的位置也不断向前。
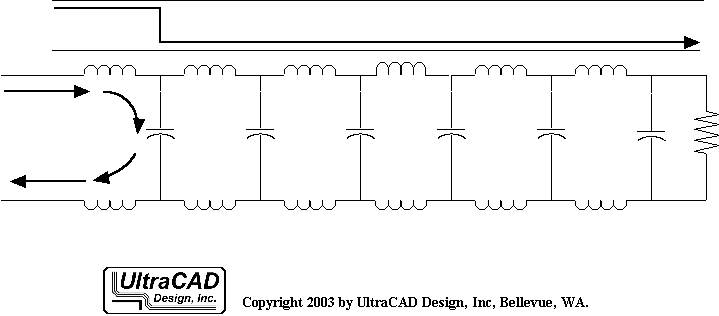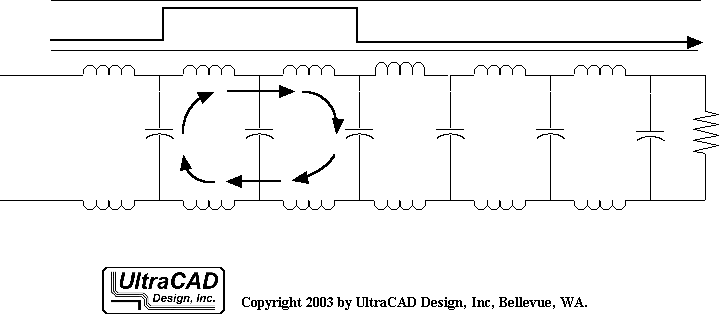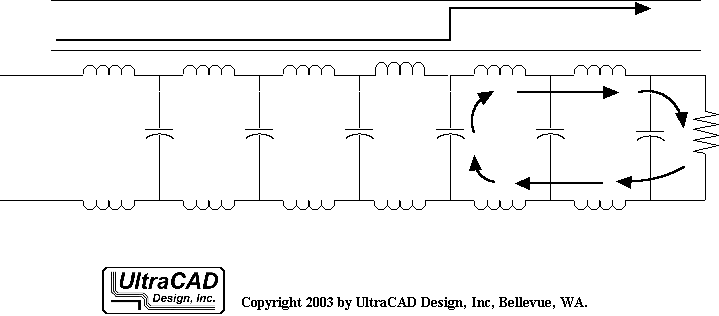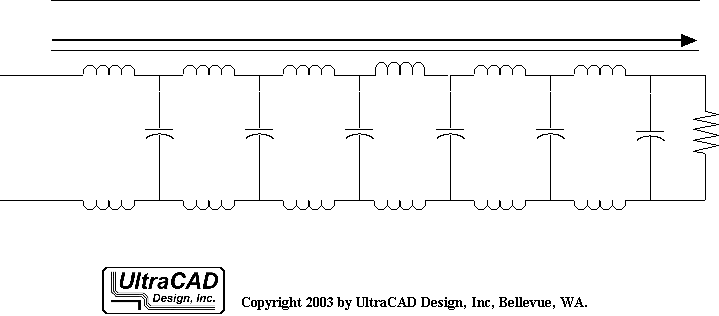
均匀传输线与平衡传输线
对传输线进行分类,如果按它的几何结构,则可通过这两个特征:沿线横截面的均匀程度、两条导线的相似与对称程度。
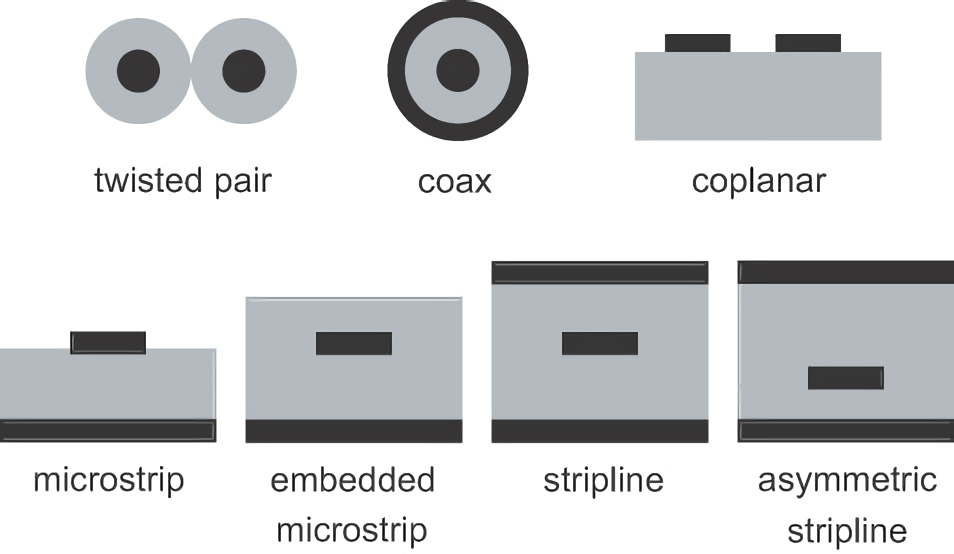
如果沿着导线,任一位置横截面都相同,则称为 均匀传输线,也称 可控阻抗传输线,例如双绞线、微带线带状线等:
信号完整性设计的一个目标,就是把所有高速互连都设计成均匀传输线,并努力减小所有非均匀传输线的长度。
另一个分类的特征,是看两条导线的相似 / 对称程度。如果两条导线形状大小都一模一样,那么它是 平衡传输线,例如双绞线(twisted pair)。而非平衡传输线的例子是同轴电缆(coax),因为它中间导线比外面一圈的横截面小。
信号传播的速度
传输线上信号传播的速度,并不取决于导体中电子的速度。
如果可知每秒通过导线截面的电子数、导线中的电子密度、导线的横截面积,就能算出导线中电子的速度。因为导体中电流(\(I\))可由以下公式计算:
其中,\(\Delta Q\) 表示 \(\Delta t\) 内流过导线的电量(单位为 \(C\)),\(q\) 表示一个自由电子所带的电量,为常数 \(1.6\times 10^{-19}C\),\(n\) 表示自由电子的密度(单位为 \(\#/m^3\)),\(A\) 表示导线的横截面积(\(m^2\))。所以可得到电子的速度(\(m/s\)):
在常见的介质中,电子的运动速度是很低的。例如一条直径为 \(1mm\) 的铜导线(铜原子间隔约为 \(1nm\),每个铜原子能提供两个自由电子,可算出自由电子密度约为 \(10^{27}/m^3\)),通过 \(1A\) 电流时电子的速度约为 \(1cm/s\)。可见,电子的速度是远低于信号传播速度的。
不仅如此,减少互连的电阻,并不能提高信号传播的速度。只有在非常极端的情况下,互连线的电阻才会轻微影响到信号传播的速度。一般情况下,导线电阻小并不意味着信号传输速度快。
信号通过电子传输的原理,是靠电子之间的相互作用。
可以把导线想象为一个装满弹珠的长管子,若在一端推动一个弹珠,在另一端将会有一个弹珠几乎同时被挤出。这里弹珠传递信号的速度,比弹珠实际运动速度要快得多。同理,导线中电子受相邻电子推动时,信号传播的快慢并不取决于电子本身的运动速度,而是受电子之间的相互扭结影响。
当信号在传输时,会在信号与返回路径之间的导体中、导体周围的空间中产生交变电磁场。而决定信号传播速度的因素,就是电磁场的建立和传播速度。
电磁场变化(场链)的速度可以由以下公式计算得到:
其中,\(\varepsilon_0\) 表示自由空间中的介电常数,取 \(8.89\times 10^{-12}F/m\);\(\varepsilon_r\) 表示材料的相对介电常数,在空气中为 1;\(\mu_0\) 表示自由空间的磁导率,取 \(4\pi\times10^{-7}H/m\);\(\mu_r\) 表示材料的相对磁导率,几乎所有互连介质都取值为 1。将以上常量代入后可得:
相比空气,其他材料的介电常数 \(\varepsilon_r\) 总大于 1,而光速约为 \(12 inch/ns\),则可说明互连中的光速总小于 \(12 inch/ns\),其实际的速度为:
相对介电常数也常简称介电常数,绝大多数聚合物的值为 4。一般来说,介电常数会随着频率的升高而降低,但在常用的 PCB 板材中变化比较小。比如,FR4 的介电常数在 3.5~4.5 之间浮动,高速板材则在 3~4 之间浮动。根据公式可以模糊推出,信号在 FR4 中的速度约为 \(6 inch/ns\)(未考虑空气介质的电磁场影响)。
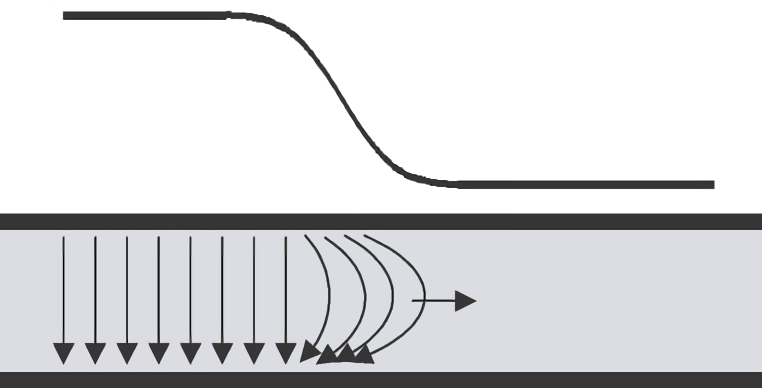
前沿的空间延伸
信号的上升沿 RT,通常表示从最大电压的 10% 变化到 90% 的时间长度。当信号在传输线上传播的时候,会把这个边沿往前推,产生一个空间延伸:
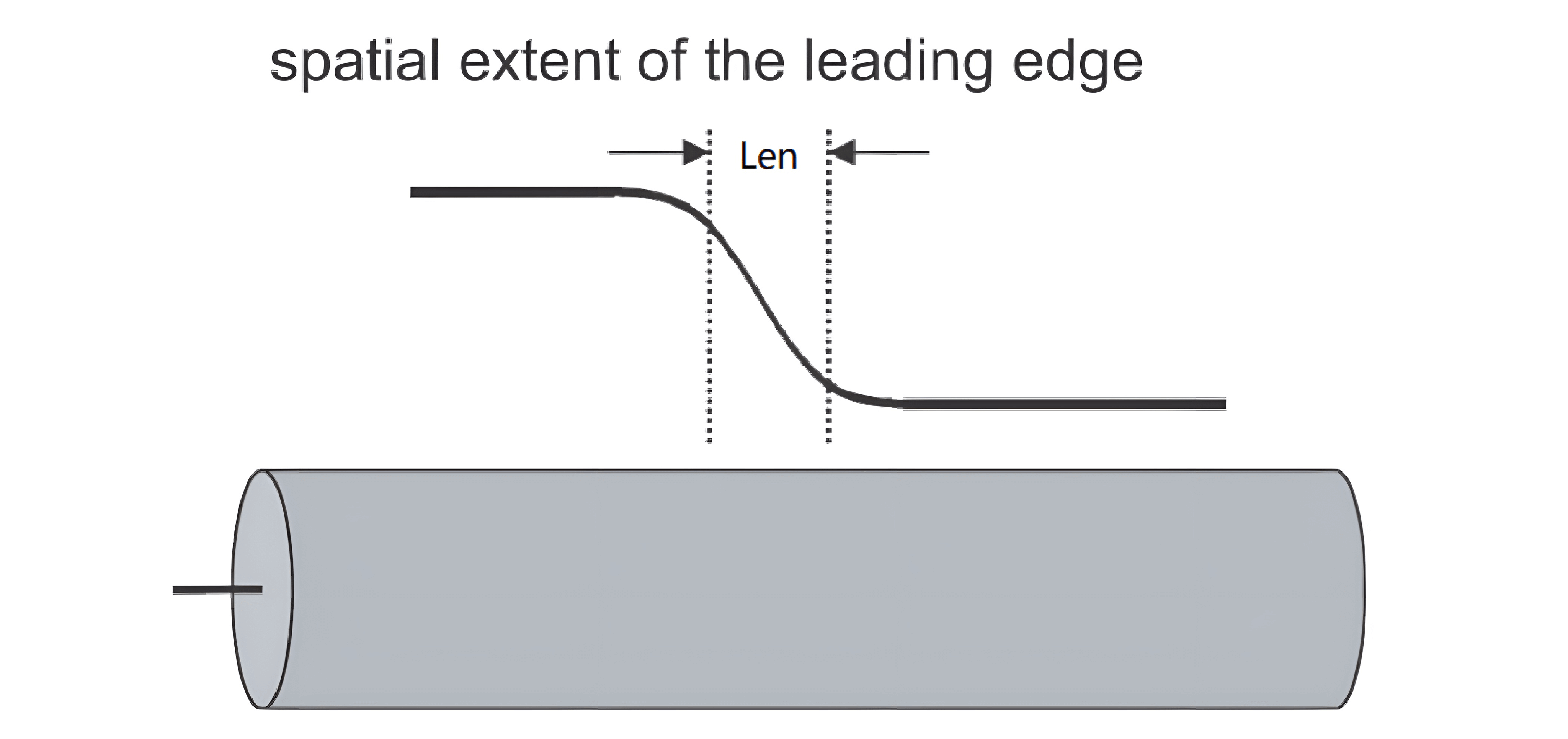
这个延伸的长度取决于信号的速度与上升沿的时间:
我们假设信号的速度为 \(6inch/ns\),信号上升沿时长为 \(1 ns\),则前沿的空间延伸长度为 \(6 inch\)。信号就推着这个 \(6 inch\) 长的边沿向前传播。
传输线的分布电容
当存在多个导体时,两两之间都会存在电容。对于 PCB 上的走线,因为空间结构长,走线导体每一部分与周围的导体都存在电容,分布在走线的整个长度区间之内,所以说传输线的电容是分布式的。当信号前进的时候,每走一步都能感受到电容的存在。
在高速互连模型中,许多现象如阻抗不连续、反射、串扰等,都与导体间的分布电容有关系。
单位长度电容
PCB 上的传输线,如果横截面积不变,那么可以使用集总电容模型,用单位长度电容来表示电容参数,这样总电容就与传输线长度成比例,这样会方便建模。
集总元件:指元件大小远小于电路工作频率相对之电磁波波长时,对所有元件之统称。对于信号而言,不论任何时刻,元件特性始终保持固定,与频率无关。
使用单位长度电容来表示传输线的电容效应的前提是:电场沿传输线的方向没有分量,即电磁波的传播近似为均匀平面波。PCB 的走线刚好满足这个条件。
传输线的分布电感
阻抗不连续、反射、串扰、地弹噪声等,也与分布电感有关。PCB 上的走线每一部分都存在自感,且和周围的导体之间都存在互感。电感分布在走线的整个长度区间内,是分布式的,信号每走一步都能感受到电感的存在。
回路电感
因为传输线可以把信号和返回路径当成一个整体看待,信号电流与返回电流同时存在且构成一个完整的电流回路,使用回路电感分析会更方便。回路电感的计算公式:
其中,\(L_{SS}\) 表示信号路径的自感,\(L_{FS}\) 表示返回路径的自感,\(L_{SFm}\) 信号与返回路径间的互感。
把回路当成一个整体,那么回路电感描述的是回路本身的电感特性,相当于回路本身的自感。
单位长度电感
为了建模方便,传输线的电感也可以等效成多个电感串联的形式。把传输线划分为许多小段的单位电感(每个小段包括信号和返回路径),长度为 \(\Delta Z\),那么 \(\Delta Z\) 越长,该区域信号和返回路径构成的区域面积越大,磁通量也越大。因为磁通量与 \(\Delta Z\) 区域面积成线性关系,进而与 \(\Delta Z\) 也称线性关系。因此只要知道单位长度的回路电感,就可以得到任意长度的回路电感。
瞬态阻抗与特性阻抗 √
根据前面的定义,我们知道阻抗是指传输线上某一位置上的电压与电流的比值。因为传输线不一定均匀,信号每走一步遇到的阻抗可能都不一样,这是一种 瞬时阻抗。
如果传输线是均匀的,那么用一个阻抗值就可以表示整个传输线的阻抗特性,这个阻抗值就称为传输线的 特性阻抗,可以用单位长度电感和单位长度电容来表示:
我们在设计 PCB 时常用的 50Ω 阻抗,指的就是特性阻抗。对 FR4 板材,当线宽为介质厚度两倍时,微带线的阻抗就为 50Ω。传输线间距相同时,特性阻抗越高,串扰的问题就越严重;而特性阻抗越低,功率损耗则越严重。所以 50Ω 是一个相对平衡的取值,后来也沿用为一般的标准,但并不意味着所有的互连都必须是 50Ω,仍可按照需求定制阻抗的大小。
特性阻抗的影响因素 √
特性阻抗的影响因素主要有 4 种:线宽、介质厚度、介电常数、走线铜箔厚度。
线宽通过影响单位长度电感和电容,从而影响特性阻抗。对电感来说,线宽越大,电感就越小,电流越分散;反之线宽越小,电流越集中,电感越大。对电容来说,线宽越大,走线和平面间的电力线越多集中在介质区域,单位长度电容也越大(类比平行板电容器,面积越大,电容越大);线宽越小,电容越小。综上所述,线宽越大,特性阻抗就越小。
介质厚度增大会导致两个导体的间距增大,从而导致互感减小,单位长度的电感就会增加,会导致传输线的特性阻抗增大。
介电常数会通过影响单位长度的电容而影响特性阻抗。节点常数增加,电容会变大,特性阻抗就越小。
铜箔厚度越大,电感越小,电容增大,因此阻抗越小。
传输线的驱动与内阻
驱动器可以等效为高速开关的电压源加上内阻:
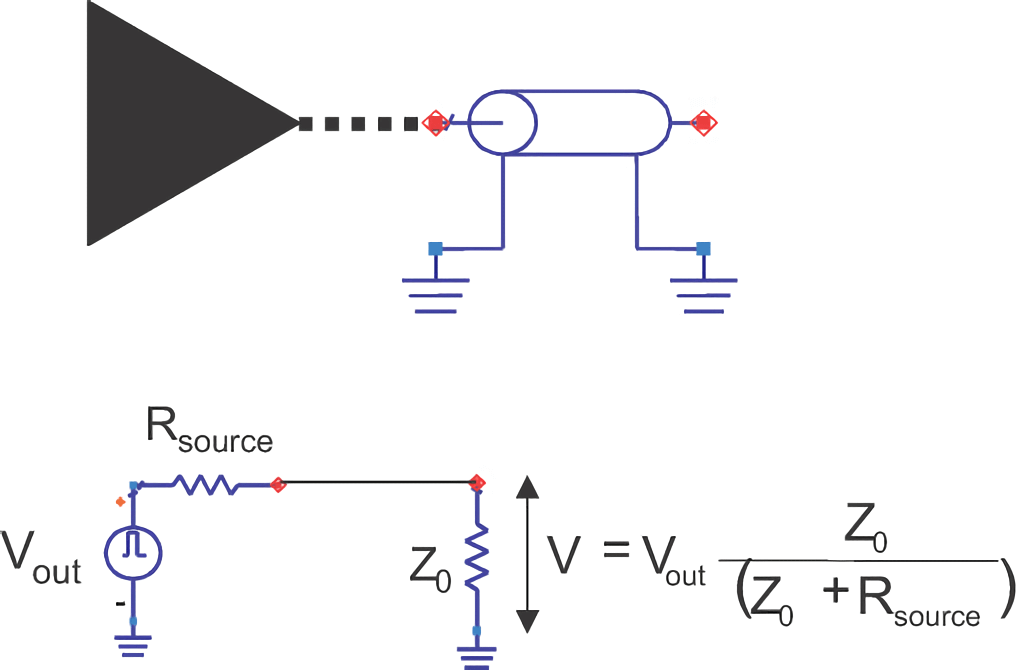
当开路时,加到传输线上的电压非常接近于源电压。内阻大小取决于器件的工艺,通常在 5-60Ω 范围内。内阻串联接入电路,可等效为一个分压器,会产生一部分压降。
所以,为了更好驱动传输线,就要使驱动器的内阻与传输线的特性阻抗尽可能小。举个例子,如果传输线的特性阻抗为 50Ω,则内阻应小于 10Ω。如果驱动器的内阻很低,那么它称为线驱动器,可以把绝大部分电压加到传输线上。
计算驱动器的内阻,可以不加传输线,驱动器直接端接外部电阻,分别测量接大电阻和小电阻时电阻两端的电压,根据等式就可计算出内阻大小。
返回路径与参考平面
电流总是在回路中流动,有去路必有回路。
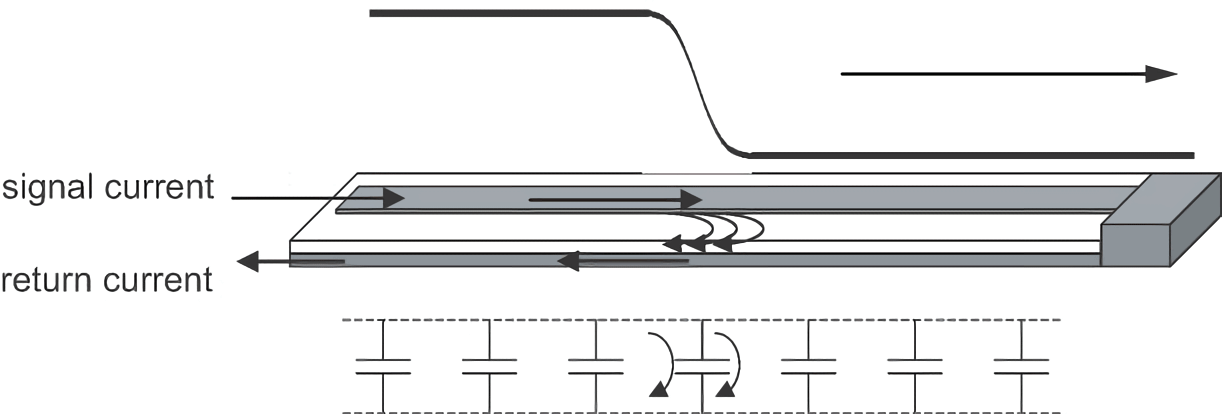
按照传输线的零阶模型,传输线信号与返回路径间是一连串小电容。电压就像浪头,边沿经过的地方,电压发生改变,就有电流经过电容流到返回路径。
一旦有信号进入传输线,就会以波的形式向外传播。电流会在信号路径、线电容、返回路径构成的回路中流动。这个电流回路的波前与电压前沿同时向外传播。所以,信号受到的瞬时阻抗就是信号电压与电流的比值。
如果返回路径是一个平面(与走线不同层),那么称为参考平面。对于表层信号线,只能与相邻的内层平面构成传输线,也可以说表层走线只有一个参考平面。而对于内层走线,有上下两个相邻平面,所以有两个参考平面。位于不同层且与信号走线重叠的平面都可以作为参考平面,构成传输线。
参考平面的返回电流并非均匀分布在整个参考平面内,而是有趋肤效应,会集中在走线正下方附近。表层微带线参考平面上的返回电流与信号电流的大小相等。对于带状线,因为有上下两个参考平面,所以返回电流会集中于信号线上下方附近,且根据到平面的距离按比例分配。信号频率越高,电流越挤近。
传输线的延时 🚧
信号需要经过一段时间才能从源端传到末端,有一定的延迟。
理想传输线的一阶模型 🚧
理想传输线有两个重要的特征:恒定的瞬时阻抗和相应的时延。一阶模型在零阶模型的基础上,把信号和返回路径导线的每一小节都抽象为回路电感:
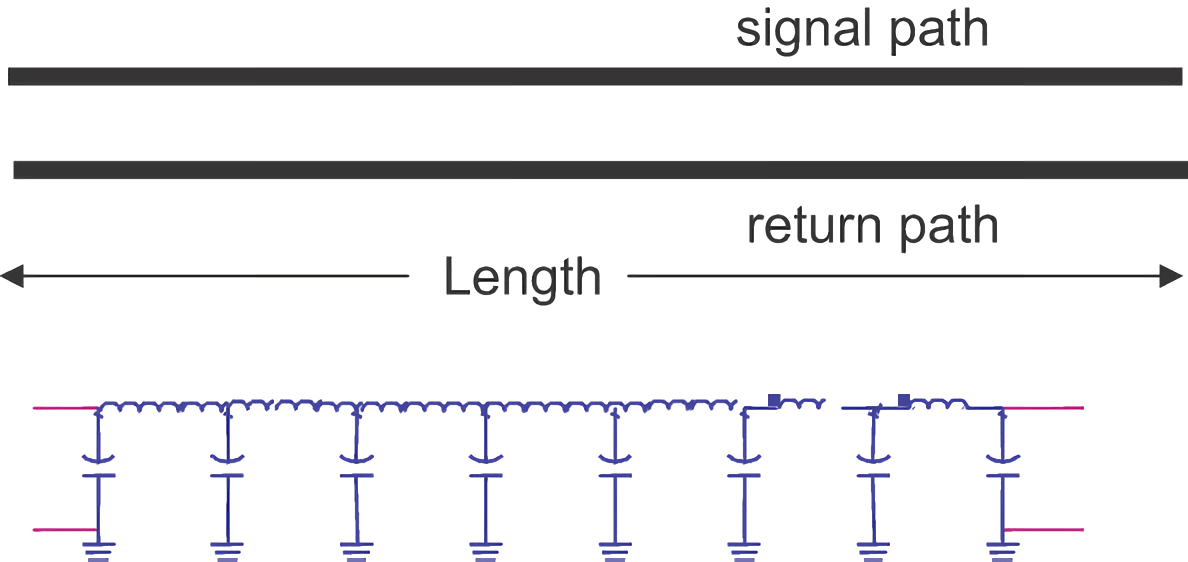
当电容和电感无穷小,LC 电路节数趋向于无穷时,单位长度电容 \(C_L\) 和单位长度电感 \(L_L\) 都趋向于常数,为传输线的线参数。如果传输线的总长为 \(Len\),那么总电容电感为:
所以,传输线的特性阻抗 \(Z_0\) 和时延 \(T_D\) 如下:
又因为传输线的特性阻抗和时延必须与零阶模型的结果相一致,所以关联起来可以得到一些等式。
因为信号的速度取决于材料的介电常数 \(\varepsilon_r\)(音 varepsilon),又取决于单位长度电容和电感,所以得出等式:
参考与致谢
- 《信号完整性与电源完整性分析》
- 《信号完整性揭秘 - 于博士 SI 设计手记》
原文地址:https://wiki-power.com/
本篇文章受 CC BY-NC-SA 4.0 协议保护,转载请注明出处。